21. Неприводимые многочлены как образующие многочлены циклических кодов. Определение общего числа элементов циклического кода. Определение числа проверочных элементов циклического кода.

Циклические коды разновидность систематических кодов, которые отличаются высокой корректирующей способностью и сравнительной простотой технической реализации.

Циклическим кодом (n, k) называется систематический код, каждая комбинация которого делится без остатка на образующий многочлен P(x) степени r =n-k. Причем каждая кодовая комбинация циклического кода представляется в виде многочлена степени  n-1.

В качестве образующих многочленов P(x) используются неприводимые многочлены. Неприводимый многочлен это такой многочлен, который делится без остатка только на самого себя или на единицу

Пример. Если кодовое слово циклического кода v(1,0)=1011101001 то соответствующий ему многочлен

В циклических кодах кодовые комбинации представляются в виде многочленов, что позволяет свести действия над кодовыми комбинациями к действием над многочленами (используя аппарат полиномиальной алгебры). Циклические коды являются разновидностью систематических кодов и поэтому обладают всеми их свойствами. Первоначально они были созданы для упрощения схем кодирования и декодирования. Их эффективность при обнаружении и исправлении ошибок обеспечила им широкое применение на практике. Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок

число проверочных элементов определяется по степени образующего многочлена.

Общее число элементов кодовой комбинации циклического кода равно n=k+r

22. Определение образующего многочлена для циклического кода.

Циклическим кодом (n, k) называется систематический код, каждая комбинация которого делится без остатка на образующий многочлен P(x) степени r=n-k. Причем каждая кодовая комбинация циклического кода представляется в виде многочлена степени  n-1.

В качестве образующих многочленов P(x) используются неприводимые многочлены. Неприводимый многочлен это такой многочлен, который делится без остатка только на самого себя или на единицу.

Пример. Если кодовое слово циклического кода v(1,0)=1011101001 то соответствующий ему многочлен

23. Алгоритм построения систематического кода.

Алгоритм построения систематического кода определяется следующим образом:

Цель процесса алгоритмизации построить код исправляющий одиночные искажения (S=1) при числе разрешенных комбинаций (в качестве примера) N_p = 2⁵ = 32 и числе информационных элементов k = 5.

1. Определение минимального кодового расстояния

d_min = 2S + 1 = 21 + 1 = 3.

2. Определение общего количества элементов кодовых комбинаций систематического кода - n.

N_p = 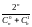= 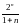где:

С - количество вариантов состояний кодовых комбинаций, когда искажение отсутствует (C = 1).

С - количество вариантов кодовых комбинаций, когда возникают одиночные искажения (в рассматриваемом примере C = =n.

3. Из формулы для определения N_p определяют общее количество элементов систематического кода

2^k = ; 2⁵ = ; 32 =

при определении n выбирают минимальный верхний предел, т.е. sup n sup n = 9, т.к. 32 должно быть меньше или равно 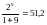, то выбирая наименьший верхний предел, получают n=9, т.е. n=9; k=5.

4. Определение числа проверочных элементов систематического кода r = n - k = 9 - 5 = 4. Для случая r=4 строится множество кодовых комбинаций N_r = 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, !001, 1010, 1011, 1100, 1101, 1110, 1111.Из полученного множества для построения проверочной подматрицы производящей матрицы выбирают пять (к=5) комбинаций (любых), вес каждой из которых p d_min-1=3-1=2. Такое подмножество определится как N₅=0011, 0101, 0110, 0111, 1001, общее же количество комбинаций, удовлетворяющих условию p 2 имеет вид N_{p 2} = 0011, 0101, 0110,0111, 1001, 1010, 1011, 1100, 1101, 1110, 1111, т.е. N_{p 2}=12.

5. Построение производящей матрицы систематического кода-G_9,5

10000	0011
(20) G9,5 = 01000	0101
00100	0110
00010	0111
00001	1001

Из общего количества разрешенных комбинаций систематического кода, содержащего 5 информационных символов N_р=2⁵ =32, пять комбинаций уже определено , т.к. они входят в состав производящей матрицы G_9,5, шестая комбинация нулевая (все элементы равны 0), осталось найти 26 производных комбинаций, которые определяются на основе суммирования по модулю 2 строк производящей матрицы, т.е. осуществляется кодирование систематического кода.

Для определения r поверочных элементов по известным информационным элементам необходимо построить проверочную матрицу, состоящую из r строк и n столбцов.

Проверочная матрица строится на основе единичной матрицы путем приписывания к ней слева подматрицы D_k,r, содержащей k столбцов и r строк. Каждая строка подматрицы D_k,r соответствует столбцу поверочной подматрицы производящей матрицы G_n,k

b11 b21 ... bk1

b12 b22 ... bk2

....................

b1r b2r ... bkr

Таким образом, проверочная матрица будет иметь вид

b11 b21 ... bk1 10 ... 0

(22) b12 b22 ... bk2 01 ... 0

................................

b1r b2r ... bkr 00 ... 1

На основании проверочной матрицы H_n,r (22) формируется алгоритм кодирования и декодирования систематического кода.

В качестве примера построим на основании производящей матрицы (20) проверочную матрицу H_9,4.

		a1	a2	a3	a4	a5		b1	b2	b3	b4
(23)		0	0	0	0	1		1	0	0	0
H9,4	=	0	1	1	1	0		0	1	0	0
		1	0	1	1	0		0	0	1	0
		1	1	0	1	1		0	0	0	1

По полученной проверочной матрице H_9,4 определяются проверочные элементы b₁, b₂, b₃, b₄ на основании следующих уравнений:

b₁ = a₅

b₂ = a₂  a₃  a₄

(24)

b₃ = a₁  a₃  a₄

b₄ = a₁  a₂  a₄  a₅