№1 Понятия математического программирования, его основные разделы. История развития.

Исследование многих процессов, в том числе и экономических, начинается с их моделирования, т.е. с отражения реального процесса через математические соотношения.

Как правило, задачи такого рода являются многовариантными. Среди множества возможных вариантов приходится отыскивать наилучший в каком-то смысле, при этом встречаются ограничения, налагаемые на физические, биологические, экономические и т.д. возможности.

Изначально, подобные задачи решались исходя из здравого смысла, а так же опыта, лица принимающего решение (ЛПР).

Такой подход нельзя считать объективным. Нет никакой уверенности в выборе наилучшего решения, а при крупных масштабах производства отклонение от наилучшего варианта, даже незначительной степени, может привести к серьезным экономическим потерям.

В связи с этим, возникла необходимость применения для анализа и синтеза математических методов специального назначения, а так же вычислительной техники.

Такие методы были объединены под общим названием: «Математическое программирование»(МП)

МП – это область высшей математики разрабатывающая теорию и численные методы, решения многокритериальных задач экстремального характера с ограничениями на переменные.

В экономических задачах принято выделять основной показатель (прибыль, доход, издержки) и находить экстремум этого показателя(max или min) при этом могут существовать как единственные, так и искусственные ограничения на различные показатели от которых зависит основной показатель.

МП включает в себя так же такие разделы как:

1. ЛП

2. Нелинейное программирование

3. Динамическое программирование

4. Стохастическое программирование

5. Теория игр

6. Теория массового обслуживания

7. Теория управления запасами и т.д.

МП позволяет решать задачи о распределении ресурсов, задачи о планировании выпуска продукции, задачи планирования товарооборота, задачи ценообразования, транспортные задачи и т.д.

МП возникло в 30-е года XX века. В 1931 году венгерский математик Б. Эгервари предложил решение задачи называемой задачей выбора (проблемы выбора). Позднее американский ученый Г. У. Кун обобщил этот метод, после чего он начал называться венгерским методом.

В 1939 году российский ученый А. В. Конторович разработал метод разрешающих множителей для задач ЛП. В 1947 году американский ученый Дж. Данциг описал один из основных методов ЛП – симплексный метод (simple - просто).

№2 Математическая модель. Этапы построения модели.

Построение математической модели любой экономической задачи включает 3 этапа:

1. Выбор переменных задач.

2. Составление системы ограничений.

3. выбор целевой функции.

Переменными задачи называются величины х1, х2, … хn, которые полностью характеризуют экономический процесс, как правило представлены в виде n-мерного вектора (n координат). Обычно их записывают в виде вектора: X=(X₁, X₂,...,X_n)

Система ограничений включает в себя уравнения и неравенства, которым удовлетворяет переменные задачи и которые следует из ограниченности ресурсов или других экономических и физических условий.

Целевая функция (функция цели) это функция переменных задачи, которая характеризует качество выполнения поставленной цели и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом:

Найти экстремум целевой функции

F(X)=f(x1, x2, … , xn) -> extr

И соответствующие ему переменные

X=(x1, x2, … , xn)

При условии, что эти переменные удовлетворяют системе ограничений

№3 Общая задача линейного программирования (ЛП). Основные определения.

Если целевая функция (*) и система ограничений (**) линейны, то задача МП называется задачей ЛП.

Выражение должно содержать переменные только в первой степени. Не должно быть произведение переменных.

В общем виде задачу ЛП можно представить следующим образом:

Найти экстремум целевой функции

F(X)=c1x1+c2x2+…+ cnxn  extr

При условии что переменные

X=(x1, x2, … , xn)

Удовлетворяют системе ограничений

Допустимым решением (допустимым планом) задачи ЛП называется любой n-мерный Х (вектор х) X=(x1, x2, … , xn) удовлетворяющий системе ограничений задачи и условиям отрицательности.

Совокупность всех допустимых решений задачи, образует область допустимых решений (ОДР)

Оптимальным решением (оптимальным планом) задачи ЛП называют такое допустимое решение из ОДР, при котором целевая функция достигает экстремума.

При использовании классических методов поиска экстремума, в первую очередь проверяется выполнение необходимого условия оно заключается в поиске точек, в которых производная либо равна нулю, либо не существует.

Для задачи ЛП производные целевой функции имеют вид:

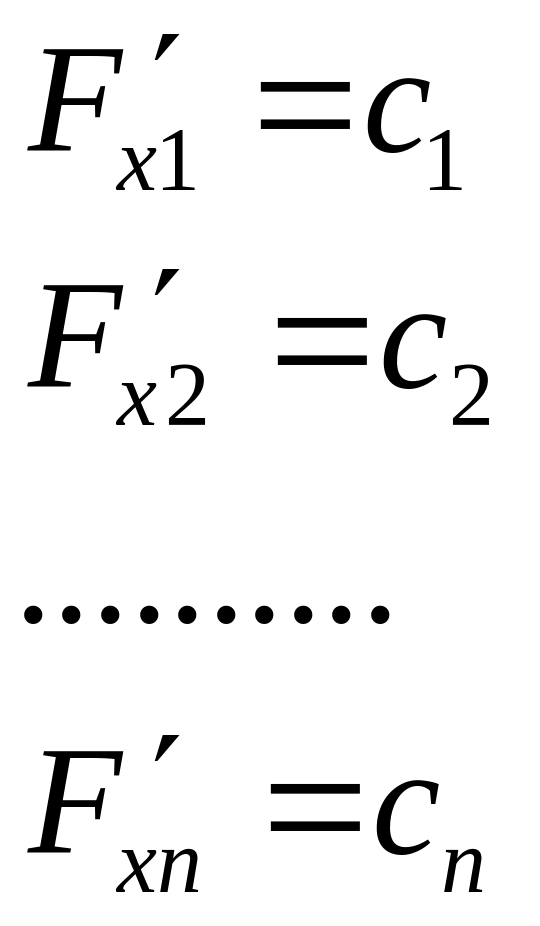
Таким образом, производные (частные производные) обращается в 0, только в том случае, если все коэффициенты целевой функции равны нулю.

С1=С2=…=Сn=0

Но при этом и сама функция, тоже превращается в ноль, а значит ее экстремум определить нельзя.

Это связано с тем, что классические методы поиска экстремума используют внутренние точки, области определения, а в задачах линейного программирования экстремум находится на границах ОДР.

Для исследования подобных задач необходимы специальные методы:

• графический метод

• симплексный метод

• метод искусственного базиса и т.д.

№4 Математические модели простейших экономических задач ЛП.(о раскрое, транспортная, распределение ресурсов)

Задача о распределении ресурсов.

Предприятие изготавливает несколько видов продукции, расходуя на это изготовления различные виды сырья. Запасы сырья ограничены. Доход, получаемый от реализации каждого вида продукции, различен. Необходимо составить такой план выпуска продукции, при котором доход предприятия был бы максимальным.

Для изготовления n видов продукции Pj используется m видов сырья Si.

Запасы сырья составляют bi. Нормативы затрат сырья на изготовление единицы продукции составляют aij. Доход, получаемый от реализации единицы продукции j-того вида, составляет Dj.

Необходимо составить такой план выпуска продукции, при котором доходж от ее реализации будет максимальным.

Построение экономико-математической модели задачи.

Обозначим xj количество единиц продукции j-го вида, запланированных к производству. Тогда целевая функция будет иметь вид.

Для изготовления всей продукции потребуется

Единиц сырья i-го вида. Поскольку его количество ограниченно величиной bi получаем неравенство.

Учитывая нормативы затрат и ограничения на ресурсы, запишем сист.неравенства.

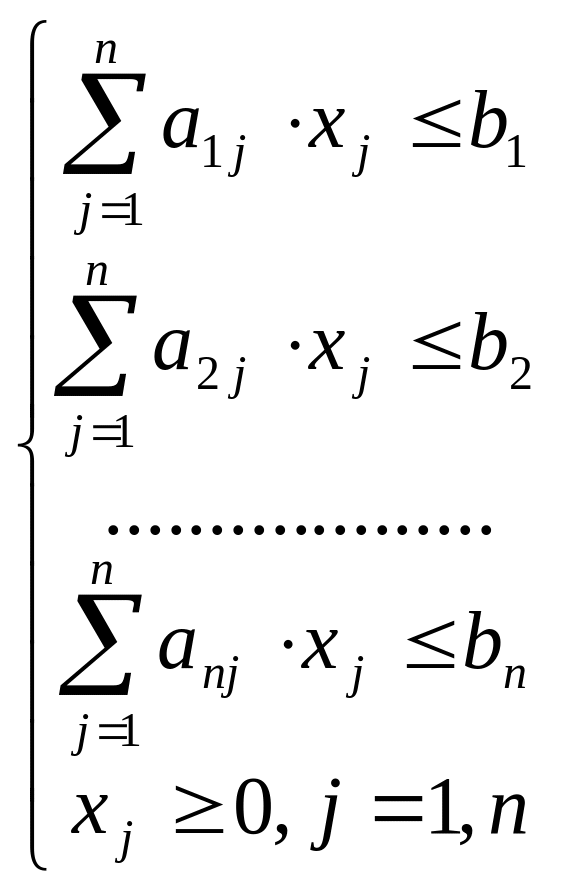
Задача о составлении рациона.

В коммерческой деятельности возникают задачи, связанные с

осуществлением рациональных закупок продуктов, обеспечива­ющих необходимый рацион питания для поддержания нормаль­ной жизнедеятельности человека, или формирование диетичес­кого питания в больницах, или задачи составления кормовых смесей на животноводческих фермах.

Задачи о рациональном питании решаются в условиях огра­ниченного ассортимента, товарных запасов, стоимости, суточ­ных норм потребления питательных веществ и их содержания в продуктах. Причем из всех возможных вариантов необходимо

выбрать самый дешевый.

Построение экономико-математической модели задачи.

Допустим, имеется набор продуктов: мясо, рыба, молоко, са хар, яйца, картофель, овощи, фрукты, хлеб, мука по ценам соответственно с1, с2,..., Сj сn, причем запасы этих продуктов огра­ничены величинами: а1 а2,..., аj, an

Содержание питательных веществ - белков, жиров, углево­дов, витаминов и минеральных солей - в 1 кг каждого продукта известны и составляют соответственно qij (i=1,m , j=1,n).

Кроме того, известны нормы суточной потребности человека в каждом питательном веществе: b1,b2,…,bi,bm.

Необходимо определить количество закупаемых продуктов

x1,x2,…,xi,xn, которое обеспечит потребность в питательных веществах каждого вида и будет иметь минимальную стоимость. Так как содержание питательных веществ в рационе должно быть не менее b1,b2,…,bi,bm., то получим систему линейных ограниче­ний: I

№5 Каноническая форма задачи линейного программирования. Различные формы записи задачи ЛП, их взаимосвязь.

В общем случае задача ЛП записывается так, что ограничениями являются как уравнения, так и неравенства. Переменные могут быть как неотрицательными, так и произвольно изменяющимися, но большинство методов основывается на канонические задачи ЛП.

Задачи ЛП считаются представлены в канонической форме, если:

1. все ограничения являются только уравнениями.

2. каждая переменная задача удовлетворяет условию неотрицательности.

Переход от задачи общего вида к канонической форме можно осуществить следующим образом:

1 этап. Переход от системы неравенств к системе уравнений.

П усть в системе содержатся неравенства вида

Если прибавить к левой части неравенства неотрицательное число, равное разности между правой и левой частью неравенства.

То знак неравенства можно заменить на знак равно. Обозначим число через

X n+1

Т огда получим уравнение

Т .о. чтобы систему неравенств вида привести к системе уравнений, необходимо ввести дополнительные неотрицательные переменные по числу неравенств системы. Нумерация этих переменных, должна продолжить уже имеющиеся и в каждое неравенство вводиться только по одной дополнительной переменной.

Так как в системе m строк, то потребуется m дополнительных, неотрицательных переменных.

X n+1, x n+2, … , x n+m

В результате введения дополнительных переменных получим систему уравнений.

Если дана система неравенств вида , то применяем аналогичный алгоритм, но дополнительные переменные входят в каждое неравенство со знаком минус.

Если система смешанного вида, т.е. содержит как уравнения, так и неравенства различного знака, то уравнение оставляем без изменений, а с каждым неравенством работаем по описанному выше алгоритму, в зависимости от знаков.

Замечание!

Дополнительные переменные не изменяют целевую функцию, т.е. входят в нее с нулевыми коэффициентами

F(X)=c1x1+c2x2+…+cnxn+0*x n+1 + 0*x n+2+…+0*x n+m

2 этап. Приведение переменных к неотрицательному виду.

Пусть Xk какая либо произвольно изменяющиеся переменная. Такую переменную всегда можно представить в виде разности двух неотрицательных переменных

Xk=xk*-xk** где xk*>=0, xk**>=0

Проведя замену в целевой функции и системе ограничений, получим задачу, содержащую только неотрицательные переменные.

Каноническую задачу ЛП можно представить в трех формах записи:

1 координатная

2 векторная

3 матричная

I координатная форма.

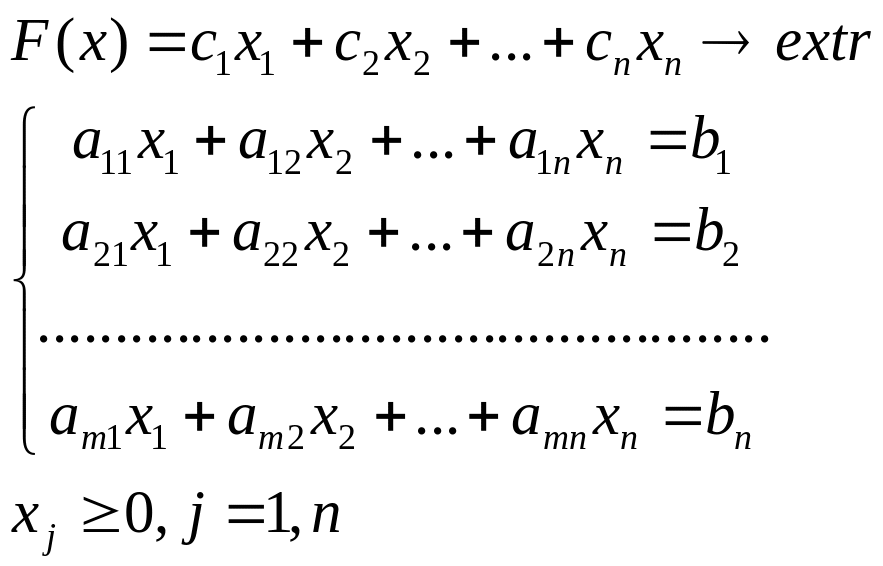
Данную задачу более кратко можно записать используя знак суммирования

II Векторная форма.

Введя след. Обозначения.

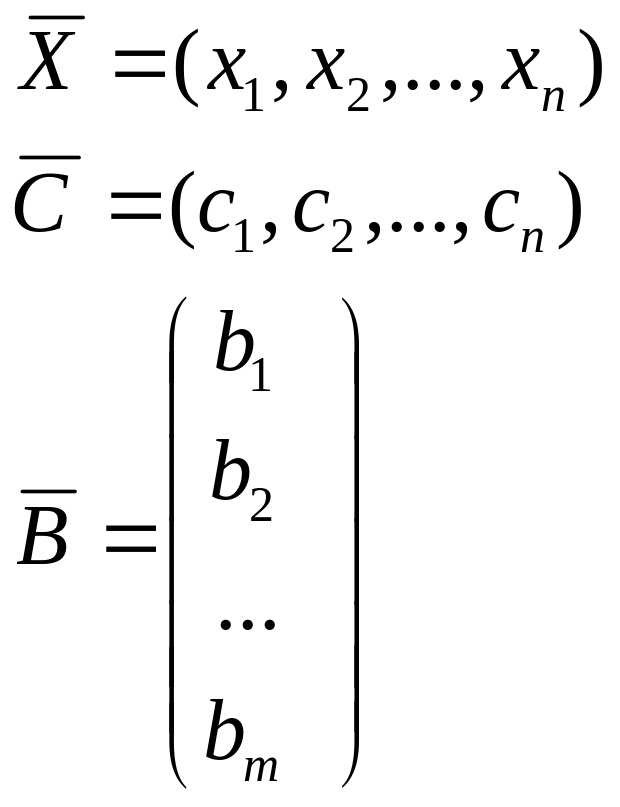
А1,А2, … ,Аn – векторы из коэффициентов система ограничений.

Получим задачу ЛП в векторной форме.

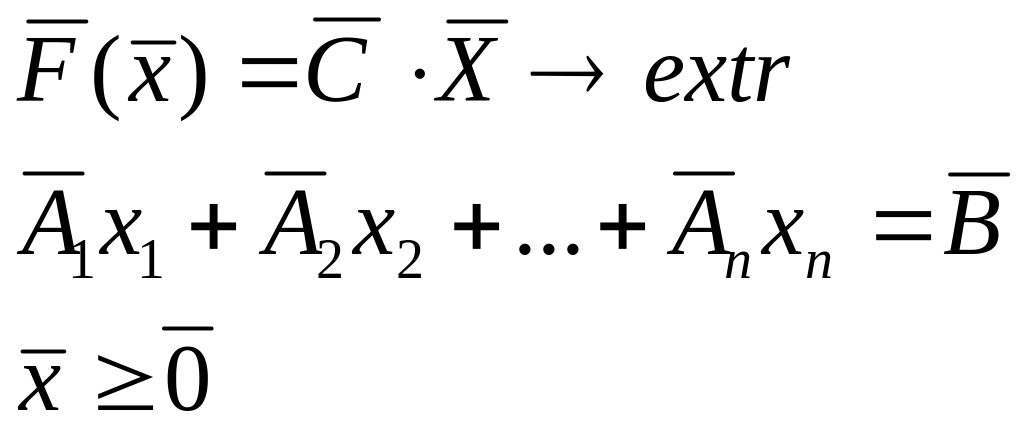
III матричная форма.

Заметим, что коэффициенты системы ограничений образуют прямоугольную матрицу.

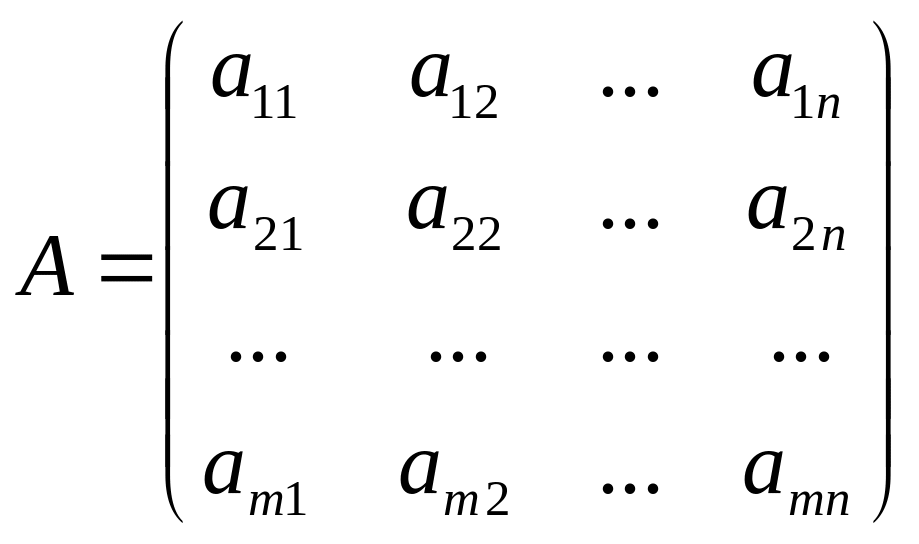
Кроме этого столбец свободных членов этой системы и вектор переменных х можно рассматривать как одностолбцовые матрицы.

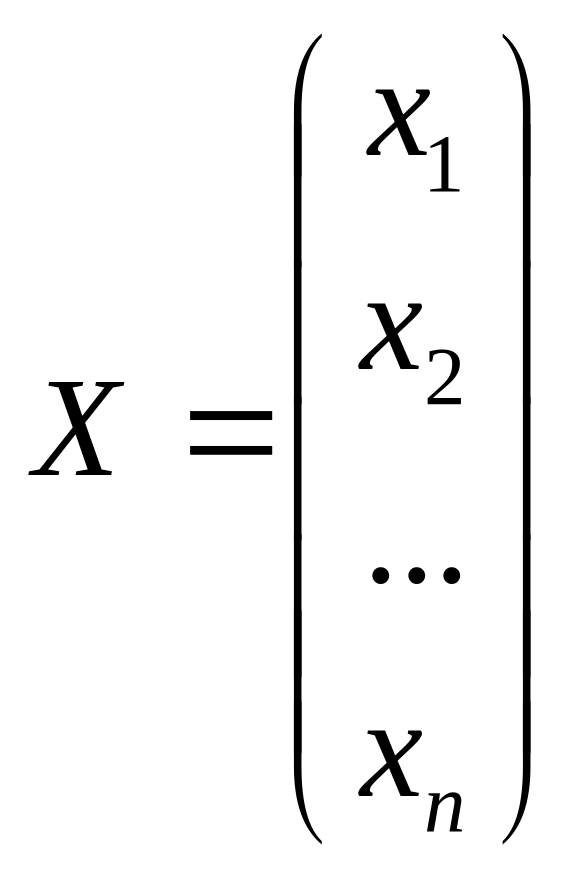
А коэффициенты целевой функции можно рассматривать как однострочную матрицу С.

Тогда в векторной форме задача примет вид.

9. Алгебраический симплексный метод. Основные положения данного метода.

Симплексный метод- это метод целенаправленного перебора опорных решений задачи, который позволяет ха конечное число шагов, либо найти оптимальное решение, либо установить, что оптимальное решение не существует.

Основное содержание симплексного метода состоит в следующем:

1. Необходимо указать способ нахождения начального опорного решения.

2. Следует указать способ перехода от одного опорного решения к другому, причем переход должен осуществляется к более оптимального или по по крайней мере не существующему решению.

3. Требуется задать критерий, который позволяет своевременно прекратить перебор решений, остановивших на оптимальном или сделать заключение , что оптимального решения нет.

Свое название симплексный метод получил от простых областей допустимых решений, которые рассматривались на ранних этапах разработки метода.

10. Алгоритм решение задачи симплексным методом(первый опорный план)

Рассмотрим алгоритм симплексного метода на примере задачи линейного программирования. Система ограничений, которой содержит неравенство вида <=

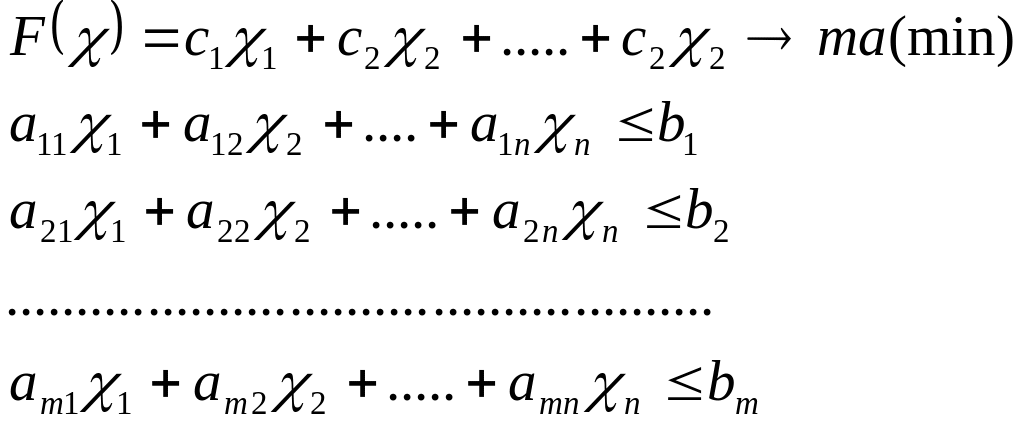
1. Приведем задачу к канонической форме. Введем m дополнительных неотрицательных переменных

х _n+1; x _n+2 ….. x _n+m

в результате получим:

F( X)= c₁ x₁+ c₂x₂+….a_1nx_n +c_nx_n +0*x_n+1 +0*x_n+2 + ……+0*x_m+n

Система

2. найдем начальное опорное решение. Выпишем матрицу из коэффициентов полученной системы ограничений

Матрица

Коэффициенты при дополнительных переменных образуют единичную диагональную матрицу- базис, поэтому x _n+1, x _n+2…..x _n+m называют базисными переменными.

Выразим базисные переменные через основные:

X _n+1=b₁-a₁₁x₁-a₁₂x₂-……-a _m x _n

X _n+2=b₂-a1x1-a₂₂x₂-……-a_2m x _n

…………………………………..

X _{m+ n}=b_m-a_m1x₁-a_m2x₂-…..-a _{m n} x _n

Прировняем к 0 основные переменные: x₁=x₂=….=x _n=0

Тогда: x_n+1=b₁

X_n+2=b₂

…………

X _{m +n}=b _m

В результате получаем начальное опорное решение

X₁= (0; 0;….;0; b₁; b₂…..b _m)

Занесем начальное опорное решение, базисные переменные, коэффициенты системы ограничений в специальную симплексную таблицу.

3.Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.

Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)

При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.

Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.

Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.

11. Алгоритм решения задачи симплексным методом ( проверка на оптимальность, определения ведущего столбца и строки, построение нового опорного плана).

Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.

Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)

При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.

Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.

Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.

Определение ведущего столбца. При решении задачи на max из всех отрицательных элементов индексной строки выбираем наибольший по модулю, этот элемент и определяет ведущий столбец.

Определение ведущей строки. Элементы столбца ЗБП делим на соответствующие элементы ведущего столбца, а результаты заносим в последний столбец таблицы.

Замечание. Делить можно числа только одного знака (+/+;-/-) т.е. в последнем столбце таблицы должны получаться только положительные значения. Если встретились числа разных знаков или деление на 0, то в столбце на соответствующем месте ставится прочерк.

Из всех элементов последнего столбца выбираем наименьший, он и определяет ведущую строку.

Определение разрешающего элемента. Разрешающий элемент находится на пересечении ведущей строки и ведущего столбца.

Заполнение нового опорного плана. В первую очередь заполняется столбец БП (базисные переменные). Базисная переменная, которая в старом плане

Оказалась на ведущей строке, покидает базис, ее место занимает переменная из ведущего столбца, а остальные переменные свое место в базисе сохраняют.

Далее заполняем строку, которая в старом плане была ведущей, для этого элементы старой ведущей строки делим на разрешающий элемент, а результаты заносим в новый план на соответствующее место.

В результате деления на месте старого разрешающего элемента окажется единица. Остальные элементы старого ведущего столбца в новом плане обнуляем. Все остальные элементы нового плана рассчитываются по формуле:

Элемент нового плана = элемент старого плана-(произведение дополняющих элементов до прямоугольника)/разрешающий элемент

Получив новый план проверяем его на оптимальность. Алгоритм повторяется до тех пор пока не получим оптимальное решение.