- •9. Алгебраический симплексный метод. Основные положения данного метода.
- •10. Алгоритм решение задачи симплексным методом(первый опорный план)
- •11. Алгоритм решения задачи симплексным методом ( проверка на оптимальность, определения ведущего столбца и строки, построение нового опорного плана).
- •13. Анализ оптимального плана симплексного метода на примере задачи планирования товарооборота.
- •Метод искусственного базиса на примере системы ограничений, содержащей уравнения.
- •Основные теоремы линейного программирования. Фундаментальная теорема и теорема об альтернативном оптимуме.
- •Геометрическая интерпретация симплекс-метода.
- •Двойственная задача линейного программирования и ее математическая модель.(не до конца!!!!)
- •21. Виды двойственных задач. Правила составления симметричных двойственных задач линейного программирования.
- •22. Виды двойственных задач. Правила составления несимметричных двойственных задач линейного программирования.
- •Основное неравенство теории двойственности. Достаточный признак оптимальности. Первая теорема двойственности.
- •24. Экономический смысл первой теоремы двойственности.
- •25. Вторая теорема двойственности. Определение двойственных оценок с помощью второй теоремы двойственности.
- •26. Определение двойственных оценок однородной задачи линейного программирования симплекс-методом.
- •31) Транспортная задача линейного программирования, ее математическая модель.
- •33. Построение начального опорного решения тз методом наименьших тарифов.
- •34. Построение начального опорного решения тз методом северо-западного угла.
- •35. Построение начального опорного решения тз методом двойного предпочтения.
- •37. Метод потенциалов тз. Проверка плана на вырожденность. Проверка решения транспортной задачи на оптимальность.
- •38. Построение нового опорного решения тз. Понятие цикла.
- •39. Анализ оптимального решения тз. Рекуррентная формула расчета целевой функции.
- •Поток Пальма. Поток Эрланга.
- •Графы состояний смо.
- •Цепи Маркова.
- •Случайные процессы. Марковские случайные процессы.
- •Уравнения Колмогорова.
Основные теоремы линейного программирования. Фундаментальная теорема и теорема об альтернативном оптимуме.
Теорема. (Фундаментальная). Если задача ЛП имеет оптимальное решение, ( в ограниченной области всегда, а в не ограниченной области в зависимости от ограниченности линейной функции), то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уровней.
Данная теорема обобщает все из рассмотренных выше случаев, утверждает, что если задача ЛП имеет оптимальное решение, то оно совпадает хотя бы с одной из вершин области допустимых решений.
Теорема. (Об альтернативном оптимуме). Если maх или min линейной функции достигает в нескольких опорных решениях, то любое оптимальное решение есть выпуклая линейная комбинация оптимальных решений.
Геометрически интерпретация данной теоремы означает. Что в случае альтернативного оптимума линии уравнения проходят через две вершины области допустимых решений и в этом случае оптимальное решение становится любая точка отрезка, соединяющая эти вершины.
Геометрическая интерпретация симплекс-метода.
Из приведенных основных теорем ЛП следует, что если задача ЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает. По крайней мере, с одним из допустимых базисных решений системы ограничений:
Необходимо найти все опорные решения (точки многогранника), множество которых является конечным;
Вычислить для каждого из опорных решений значения целевой функции
Сравнить значения целевой функции в каждой из опорных решений и выбрать оптимальное (максимальное или минимальное)
Теоретически данная схема приведет к нахождению оптимального решения, но практически её осуществление связано с большими вычислительными трудностями. Даже в задаче с двумя переменными число опорных решений может оказаться очень большим, а при большом значении n оно может достигать огромных чисел и практическое осуществление указанного перебора всех опорных решений станет невозможным. Эти вычисленные трудности возникают в результате того, что рассмотренная принципиальная схема связана с простым перебором опорных решений, т.е. в этой схеме не принимается во внимание тот факт, на сколько новое испытуемое опорное решение улучшает значение решения целевой функции и приближает нас к оптимальному решению. Если же указанный перебор опорных решений производить направлении., т.е. на каждом из шагов улучшая ( или, по крайней мере, не ухудшая) значения целевой функции то число перебираемых опорных решений можно резко сократить, что в конечном итоге приводит к весьма существенному сокращению числа шагов при отыскивании оптимума целевой функции. При использовании такой схемы, в отличие от первой, каждое последующее опорное решение выбирается таким образом, чтобы оно было лучше, (или по крайней мере, не хуже) предыдущего. Именно на каждом из шагов значение целевой функции улучшается ( или, по крайней мере, не ухудшается).
Сравним результаты применения схем простого и направленного перебора на конкретном примере.
Р![]() ассмотрим
случай, когда область допустимых решений
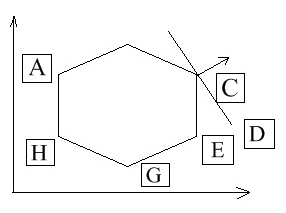
задачи ЛП (рис.1) представлена замкнутым
выпуклым многоугольником ABCDEGH.
Предположим, что первым из базисных
решений которое найдено, является вектор
,компоненты которого
соответствуют координатам угловой
точки А рассматриваемого многоугольника.
При использовании схемы прямого перебора
решений, мы, последовательно переходя
от вершины к вершине ( начиная от вершины
А и заканчивая вершиной Н), вынуждены
бы были испытать все семь вершин
многоугольника. Предположим, что
применение данного способа позволило
нам определить. Что оптимум достигается
в точке С.
ассмотрим
случай, когда область допустимых решений
задачи ЛП (рис.1) представлена замкнутым
выпуклым многоугольником ABCDEGH.
Предположим, что первым из базисных
решений которое найдено, является вектор
,компоненты которого
соответствуют координатам угловой
точки А рассматриваемого многоугольника.
При использовании схемы прямого перебора
решений, мы, последовательно переходя
от вершины к вершине ( начиная от вершины
А и заканчивая вершиной Н), вынуждены
бы были испытать все семь вершин
многоугольника. Предположим, что
применение данного способа позволило
нам определить. Что оптимум достигается
в точке С.
Из чертежа видно, что, применяя метод направленного перебора, мы от вершины А перешли бы к вершине В, а затем к оптимальной вершине С, перебрав таким образом всего 3 точки, (вместо 7. Которые мы должны были бы испытать, используя метод простого перебора).
В то же время очевидно, что для практического применения метода направленного перебора необходимо знать:
Алгоритм определения какого-либо первоначального допустимого решения задачи
Алгоритм перехода к лучшему ( или, точнее, не к худшему) решению
Признак, указывающий на , то, что найденое решение относительно.
Фундаментом универсального метода решения задач ЛП. Который называется симплекс-методом, является метод направленного перебора.
Геометрическая интерпретация симплекс-метода состоит в последовательном переходе от одной вершины многогранника к другой ( от первоначально выбранной вершины к одной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее или, по крайней мере, не худшее значение). Этот процесс происходит до тех пор, пока не будет найдено оптимальное решение-вершина, где достигается оптимальное оптимальное решение-вершина, где достигается оптимальное значение функции (если задача имеет конечный оптимум).
Идея симплекс-метода разработана русским учёным Л.В. Канторовичем в 1939 году. На основе этой идеи американский учёный Д.Данциг в 1949 году разработал симплекс-метод, позволяющий решать любую задачу ЛП.
В настоящее время на основе этого метода разработан пакет программ с применением которого решается задачи ЛП.
Рис. 1.Геометрическая интерпретация симплекс-метода.