
- •1. Основные определения теории кодирования. Кодовое слово. Длина кодовой комбинации. Системы счисления.
- •2. Алгоритм функционирования синдрома приемного устройства кодов Боуза-Чоудхури-Хоквингема.
- •3. Двоичные коды. Двоично-десятичные коды. Кол Грея
- •4. Методика построения множества кодовых комбинаций кодов Боуза-Чоудхури-Хоквингема для случая обнаружения и исправления тройных искажений.
- •5. Комбинаторные коды. Конфигурация комбинаторных кодов.
- •6. Методика построения множества кодовых комбинаций кодов Боуза-Чоудхури-Хоквингема для случая обнаружения и исправления двойных искажений.
- •7. Корректирующие коды. Равномерные коды. Неравномерные коды. Двухпозиционные коды. Многопозиционные коды.
- •8. Образующий многочлен кода Боуза-Чоудхури-Хоквингема. Методика построения образующего многочлена.
- •9. Блочные коды. Систематические и несистематические коды.
- •10. Методика построения дополнительной и производящей матриц кодов Боуза-Чоудхури-Хоквингема.
- •11. Основные характеристики корректирующих кодов. Избыточность корректирующих кодов. Кодовое расстояние. Вес кодовой комбинации.
- •12. Определение числа проверочных, и информационных элементов кода Боуза-Чоудхури-Хоквингема.
- •13. Кодовое расстояние в корректирующих кодах для обнаружения и исправления искажений.
- •14. Коды Боуза-Чоудхури-Хоквингема. Общая характеристика. Число исправляемых искажений, кодовое расстояние.
- •15. Корректирующие коды с обнаружением искажений, применяемых в системах теледоступа к вычислительным ресурсам и системах передачи и обработки информации.
- •16. Методика и алгоритм обнаружение и исправление одиночных искажений в циклических кодах
- •17. Систематические коды. Процесс образования полного множества линейно-независимых кодовых комбинаций.
- •18. Методика и алгоритм обнаружение и исправление двойных искажений в циклических кодах.
- •19. Методика и алгоритм построения производящих и проверочных матриц систематических кодов
- •20. Алгоритм построения циклических кодов.
- •21. Неприводимые многочлены как образующие многочлены циклических кодов. Определение общего числа элементов циклического кода. Определение числа проверочных элементов циклического кода.
- •22. Определение образующего многочлена для циклического кода.
- •23. Алгоритм построения систематического кода.
- •24. Циклические коды. Основные преобразования циклических кодов.
- •25. Построение систематического кода на основе исходных комбинаций простого двоичного кода
- •26. Декодирование принятых комбинаций кода Хэмминга.
- •27. Алгоритм декодирования принятых комбинаций систематического кода.
- •28. Методика построения кодов Хэмминга
- •29. Алгоритм обнаружения ошибок в принятых кодовых комбинациях систематических кодов.
- •30. Построения производящих и проверочных матриц кодов Хэмминга.
- •31. Код Хэмминга. Общие положения. Характерные особенности
- •32. Алгоритм построения систематических кодов, исправляющих одиночные искажения.
- •33. Определение общего числа элементов кодовых комбинаций систематических кодов. Определения числа проверочных элементов систематических кодов.
- •34. Алгоритм построения производящих и проверочных матриц систематических кодов.
- •35. Определение минимального кодового расстояния в кодах Хэмминга. Определение общего числа элементов кодовых комбинаций кодов Хэмминга, числа информационных и числа проверочных элементов.
- •36. Исправление одиночных искажений в циклических кодах.
- •37. Процесс алгоритмизации построения систематических кодов.
- •38. Две леммы о построении кодовых комбинаций блочных разделимых кодов.
- •39. Коды перестановок, размещений, сочетаний. Взвешенные двоично-десятичные коды 8421, 2421, 7421.
- •40. Алгоритм процесса декодирования систематических кодов, исправляющих одиночные искажения.
- •41. Классификация и кодирование технико-экономической информации. Основные понятия классификации технико-экономической информации.
- •42. Международные классификаторы. Гибкость системы. Емкость системы. Степень заполненности системы.
- •43. Иерархические и многоаспектные классификационные системы технико-экономической информации.
- •44. Классификатор материальных ресурсов для обеспечения производства.
- •45. Кодирование технико-экономической информации. Понятие унифицированной системы документации.
- •46. Единая система классификации и кодирования технико-экономической и социальной информации (ескк) Российской Федерации.
1. Основные определения теории кодирования. Кодовое слово. Длина кодовой комбинации. Системы счисления.
Под кодом понимают совокупность знаков (символов) и система определяющих правил, при помощи которых может представлено конкретное сообщение. Сам процесс кодирования определен как преобразование информации при ее хранении, передаче и обработке в виде системы отображений и установления соответствий между элементами сообщений и сигналами, при помощи которых эти элементы можно зафиксировать.
К основным характеристикам кодов относят элементы кодовых комбинаций и кодовое слово. Под кодовым словом понимают - множество упорядоченных элементов кодовой комбинации (кортеж) в цикле преобразования сообщений. Так, например, если обмен данными в каждом цикле (при передаче одного элемента естественного языка) осуществляется 8 битами, то кодовая комбинация, состоящая из конкретного множества единиц и нулей, и составляет кодовое слово. Число символов в кодовом слове называется длиной кодовой комбинации (длина кодового слова). Для отображения элементов кодовых комбинаций могут использоваться буквы, цифры, различные знаки и символы. Число различных значений m, которое может принимать каждый кодовый символ, называется основанием кода.
независимо от системы счисления с основанием m, кодовое слово k = (an-1, an-2, ... ,ao) длины n можно определить как
k
= an-1
mn-1 + an-2
mn-2 + ... + a1
m1 + a0
m0 =
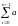 i
mi
i
mi
Для оперирования в вычислительных и иных системах обработки данных, работающих с двоичными числами, символы естественного языка переводятся в двоичную систему счисления.
В компьютерных системах зачастую используется восьмеричная система счисления, когда для представления любого десятичного числа используют всего восемь десятичных элементов кода (0,1,2,3,4,5,6,7) и перевод из восьмеричной системы счисления в двоичную производится по правилу, каждый элемент восьмеричной цифры заменяется трехразрядным двоичным числом.
Наиболее часто в компьютерных системах, а также в системах передачи данных применяется двоично-десятичная система счисления. В этой системе каждая цифра (элемент десятичного числа) отображается четырех разрядным двоичным числом.
2. Алгоритм функционирования синдрома приемного устройства кодов Боуза-Чоудхури-Хоквингема.
Для обнаружения и исправления искажений в кодовых комбинациях БЧХ алгоритм функционирования синдрома приемного устройства аналогичен алгоритму обнаружения и исправления искажений в простейших циклических кодах с минимальным кодовым расстоянием dmin2S+1.
Алгоритм обработки и исправления искажений кодовой комбинации кодов БЧХ целесообразно рассмотреть на конкретном примере.
Пример. Цель - произвести исправление двойного искажения (S=2) в принятой кодовой комбинации кода БЧХ с общим числом элементов n=15 и числом информационных элементов k=7.
Для примера построим кодовую комбинацию множества кодов БЧХ на основании производящей матрицы G15,7. рассмотренной несколько выше. Сложением по модулю 2 трех строк производящей матрицы G15,7 образуется следующая кодовая комбинация кода БЧХ
001000000111010
010000001110100
100000011101000
111000010100110
Предположим, что при передаче кодовой комбинации кодов БЧХ Ni(1,0) = 111000010100110 произошло двойное искажение в двух соседних элементах (3 и 4 элементы младших разрядов). Принятая кодовая комбинация будет иметь вид Ni(1,0)=111000010101010.
Для исправления искажений в принятой кодовой комбинации необходимо принятую комбинацию разделить на образующий многочлен P(x)=P(1,0)=111010001. Образующий многочлен взят из приведенного примера, где и описано его построение.
11100010101010 111010001
111010001
100111010
111010001
111010111
111010001
1100 остаток p = S = 2, т.е. вес остатка равен числу исправляемых искажений. Напоминаем, что для нахождения искаженных элементов кодовых комбинаций кодов БЧХ и их исправлений необходимо выполнение условия, чтобы вес остатка (количество единиц в остатке) был меньше или равен числу исправляемых искажений, т.е. pS. После чего принятая комбинация суммируется с полученным остатком по модулю 2. Полученная сумма и даст исправленную кодовую комбинацию. Если pS, то производится циклический сдвиг принятой комбинации на один разряд влево, и вновь образованная кодовая комбинация делится на образующий многочлен. Эта операция повторяется до тех пор, пока не будет выполняться условие pS. Затем производится последовательно сдвиг последней кодовой комбинации вправо на столько разрядов, на сколько была сдвинута влево искаженная кодовая комбинация. В результате циклического сдвига образуется исправленная кодовая комбинация.
Итак, в рассмотренном примере вес остатка равен числу исправляемых искажений (p=S=2), что удовлетворяет условию pS. Производя суммирование по модулю 2 принятой искаженной кодовой комбинации с полученным остатком, производится исправление искажений
111000010101010
1100
111000010100110 исправленная комбинация.
Для получения полной картины исправления искажений необходимо рассмотреть несколько вариантов.
