2. Потенциал. Работа по перемещению заряда в электростатическом поле.

2. 1. Потенциал, разность потенциалов электростатического поля?

Потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля:

(1.6)

Разность потенциалов:

(1.7)

1. 2. Связь между напряженностью и потенциалом электростатического поля.

, или (1.8)

Рис. 1.7

т. е. напряженность поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал имеет одно и то же значение (рис. 1.7).

2. 3. Работа электростатического поля при перемещении заряда.

Работа при перемещении заряда Q₀ из точки 1 в точку 2 находится (рис. 1.13) из определения работы электростатического поля и закона Кулона , тогда

(1.14)

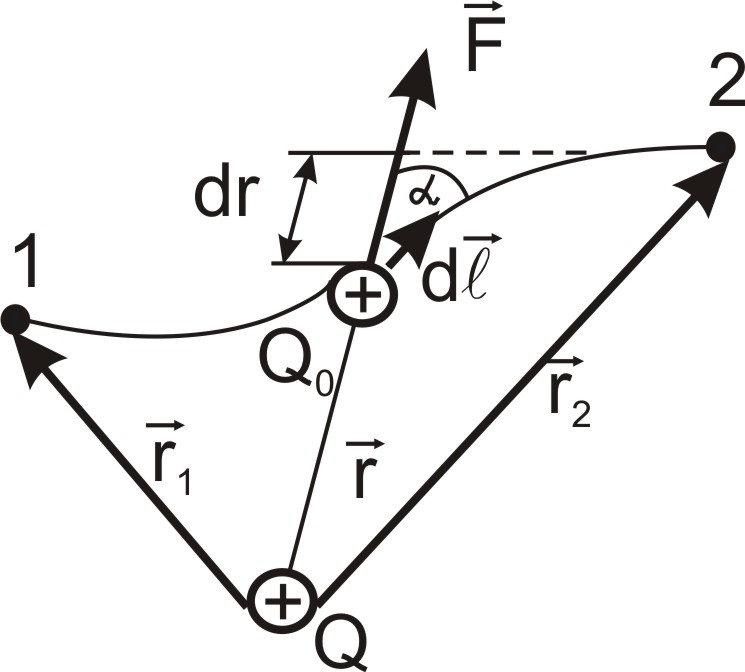
Рис. 1.13

Работа сил поля при перемещении заряда Q₀ из точки 1 в точку 2 может быть записана также в виде

(1.16)

Работа электростатического поля не зависит от траектории движения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

2. 4. Циркуляция вектора напряженности электростатического поля.

Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути равна , где - проекция вектора Е на направление элементарного перемещения.

(1.15)

Интеграл называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным. Из обращения в нуль циркуляции вектора следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

Работа электростатического поля, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути , равна нулю, т. е.

2. 5. Вектор электрического смещения.

Вектор электрического смещения для электрически изотропной среды равен

(1.17)

где -диэлектрическая проницаемость среды, показывающая как слоем диэлектрика ослабляется поле по сравнению с вакуумом.

Вектор напряженности , переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Линии вектора могут начинаться и заканчиваться на любых зарядах – свободных и связанных, в то время как линии вектора – только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора проходят не прерываясь.