I. 4. Применение закона Био – Савара – Лапласа к расчету магнитных полей.

По формуле (2.3) можно рассчитать магнитные поля простых тел. Магнитное поле, создаваемое отрезком c током _{, в точке А.}.

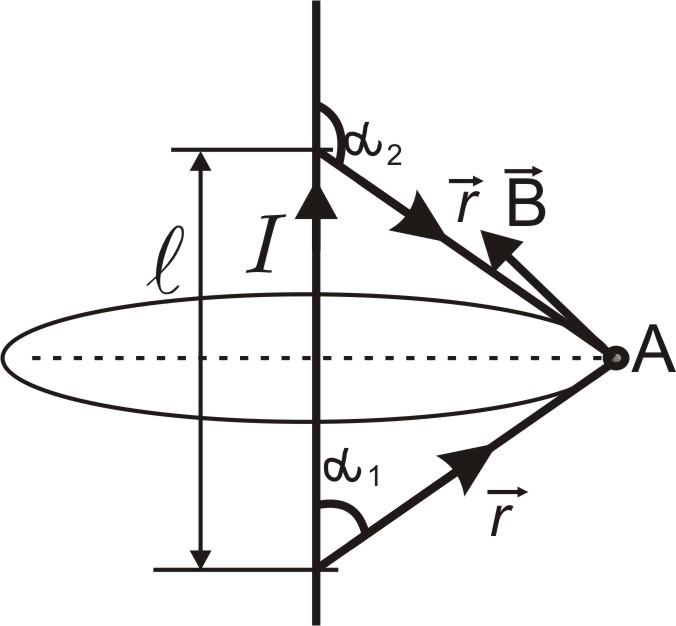
Рис. 2.5

(2.4)

Магнитное поле, создаваемое бесконечно длинным проводником, в точке А.

(2.5)

Рис. 2.6

Магнитное поле, создаваемое в центре кругового витка с током , в точке О.

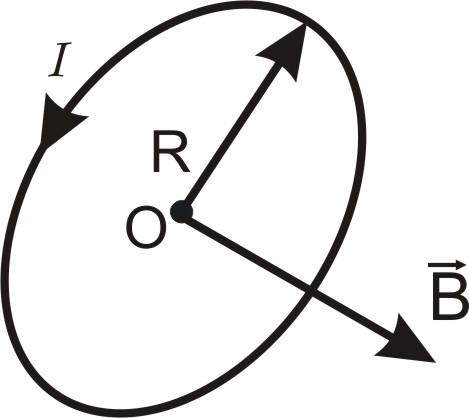
Рис. 2.7

(2.6)

II. 14. Циркуляция вектора магнитного поля в вакууме. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ).

Циркуляцией вектора по заданному замкнутому контуру называется интеграл

– вектор элементарной длины контура, направленный вдоль обхода контура, В₁ = В cos α – составляющая вектора в направлении касательной к контуру (с учетом выбранного направления обхода), α – угол между векторами и .

II. 14. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ).

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ): циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной µ₀ на алгебраическую сумму токов, охватываемых этим контуром

(2.13)

где n – число проводников с токами, охватываемых контуром  произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например (рис. 2.20):

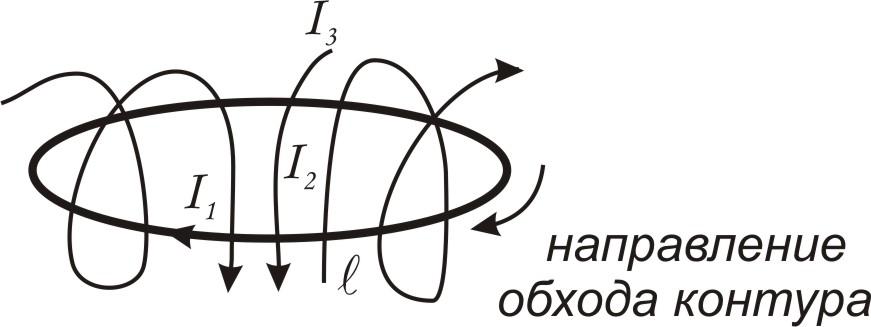
Рис. 2.20

II. 15. Поток вектора магнитной индукции.

Потоком вектора магнитной индукции (магнитным потоком) через площадку называется скалярная физическая величина, равная

(2.14)

где B_n = B cos α – проекция вектора на направление нормали к площадке (α – угол между векторами и ), – вектор, модуль которого равен dS, а направление его совпадает с направлением нормали к площадке.

Поток вектора магнитной индукции Ф_в через произвольную поверхность S равен

Рис. 2.21

II. 15. Теорема Гаусса для магнитного поля .

Теорема Гаусса для поля : поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(2.15)

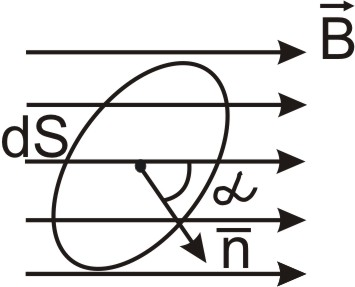
Рис. 2.21

II. 11. Закон Ампера. Покажите взаимодействие параллельных токов.

Ампер установил, что сила d,с которой магнитное поле действует на элемент проводника с током , находящийся в магнитном поле, равна

(2.9)

где – вектор, по модулю равный dl и совпадающий по направлению с током, – вектор магнитной индукции, _{- сила тока в проводнике (рис. 2.13).}

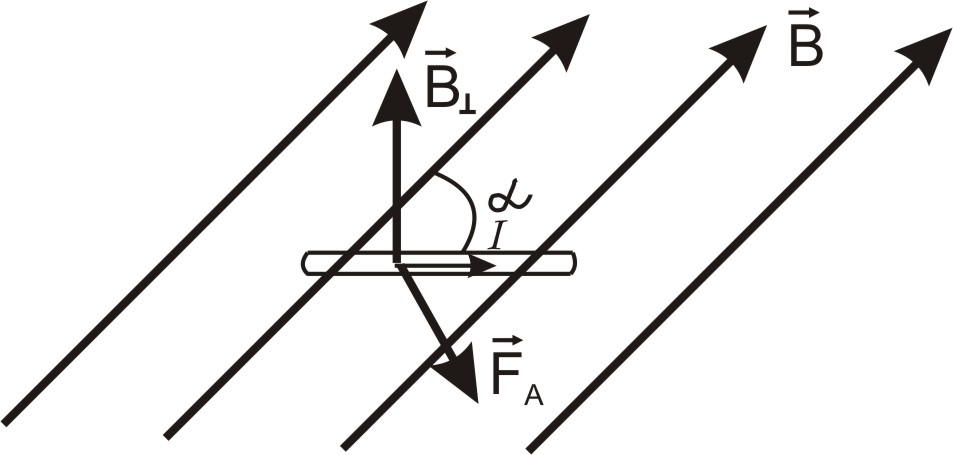
Рис. 2.14

Направление вектора может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый под углом 90⁰ большой палец покажет направление силы, действующей на проводник с током, т. е. силы Ампера.