§ 22. Електричний резонанс. Резонанс напруг

і струмів

Оскільки змінний електричний струм є вимушеними електричними коливаннями, тому природно припустити, що в електричному колі змінного струму можливий резо­нанс.

Амплітуда сили струму при вимушених коливаннях в контурі під дією зовнішньої гармонічно змінної напру­ги визначається, як відомо, формулою

Проаналізуємо цю формулу. При заданій напрузі U_m і значеннях R, L і С сила струму залежить від частоти коливань. Приіндуктивний опір дорівнює нулю,

а ємнісний — нескінченно великий і сила струму в колі дорівнює нулю. Сила струму в колі дорівнює нулю і при нескінченно великій частоті (), оскільки в цьому

випадку. Сила струму буде незначною

при малих і великих частотах. Очевидно, максимальне зна­чення сили струму буде при такій частоті соо, при якій знаменник у формулі матиме найменше значення. Це буде тоді, коли вираз у дужках під коренем стане рівним нулю, тобто

(22.1)

При виконанні умови (22 1), тобто коли індуктивний опір котушки дорівнює ємнісному опору конденсатора і по колу йде однакова сила струму, однаковими будуть і амплітуди коливань напруги на конденсаторі та котушці. Коливання напруги на котушці і конденсаторі проти­лежні за фазою, тому сума напруг на них при виконанні умови (22.1) в будь-який момент часу дорівнює нулю. В результаті напруга на активному опорі під час резо­нансу буде дорівнювати повній напрузі:. Це озна­чає, що сила струму в колі визначається лише активним опором R, дії індуктивності і ємності взаємно компен­суються. Це явище називається резонансом напруг. Сила струму в колі досягає максимального значення

Оскільки активний опір R електричних кіл звичайно ма­лий, то під час резонансу сила струму може бути дуже великою.

Із формули (22.1) можна визначити частоту, при якій настає резонанс (резонансну частоту):

(22.2)

Ця частота збігається з власною частотою вільних коливань у контурі з малим активним опором (див. фор­мулу 10.5).

Отже, явище електричного резонансу полягає в різкому зростанні амплітуди вимушених коливань сили струму в контурі з малим активним опором, коли збігаються частоти зовнішньої змінної напруги з власною частотою коливань контуру.

У випадку механічних коливань резонанс проявляється тим чіткіше, чим менші втрати енергії в системі (чим мен­ше тертя). Аналогічно до цього електричний резонанс проявляється тим сильніше, чим менше R, тобто чим менші енергетичні втрати в колі. Якщо й->-0, резонансне зна­чення амплітуди сили струму необмежено зростає: /_рез—>-оо. Навпаки, зі збільшенням R максимальне значення амплі­туди сили струму зменшується. І коли R дуже великий, резонанс взагалі не виникає, аналогічно до того, як при великому терті не виникає резонанс в механічній системі. Залежність амплітуди сили струму від частоти при різ­них активних опорах R показана на малюнку 36, де

Під час резонансу амплітуда напруги на котушці індуктивно­сті U_L дорівнює амплітуді напру­ги на конденсаторі U_c. Значення цієї напруги можна знайти як добуток амплітуди сили струму під час резонансу на індуктивний або ємнісний опір:

Але

тоді

(22.3)

З рівняння (22.3) випливає, що амплітуда напруги на котушці індуктивності і конденсаторі під час резонансу

вразів більша за амплітуду напруги, прикладеної

до кола. Якщо активний опір і ємність кола дуже малі, то може значно перевищити одиницю. Наприклад, для(таке коло легко

скласти) дістанемо . Цей приклад показує,

що в момент резонансу напруга на конденсаторі і котушці індуктивності може в сотні разів перевищити напругу, прикладену до кола. Це явище аналогічне до виникнення великих навантажень на окремі частини механічної систе­ми під час резонансу. Як під час механічного резонансу можливе руйнування системи, так і під час електричного можливе руйнування електричного кола, наприклад, елек­тричний пробій конденсатора, перегрівання провідників і пробій ізоляції.

Під час резонансу, як це випливає з рівняння (20.6), зсув фаз між коливаннями сили струму і напруги дорівнює

нулю. Дійсно, оскільки , то і

Це легко пояснити. Коливання напруги на котушці індук­тивності і конденсаторі завжди відбуваються у протифазі і амплітуди цих напруг однакові. В результаті напруги на котушці і конденсаторі повністю компенсують одна однуі спад напруги відбувається лише на актив-

ному опорі. А на активному опорі фази коливань сили струму і напруги збігаються.

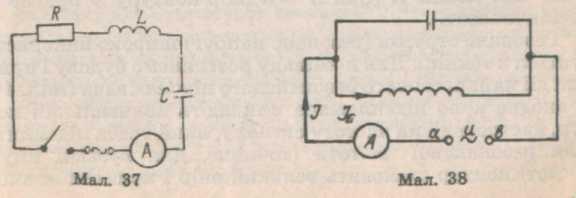
Явище резонансу в електричному колі можна спостері­гати на такому досліді. До електричного кола (мал. 37) з послідовно увімкнутих резистора, котушки індуктив­ності, конденсатора і амперметра змінного струму приєд­нують генератор змінної напруги регульованої частоти, наприклад генератор звукової частоти. Паралельно до кон­денсатора чи котушки індуктивності вмикають вольтметр змінного струму. Збільшуючи поступово частоту коливань генератора, можна спостерігати, що сила струму в колі і напруга на конденсаторі (чи котушці індуктивності) спо­чатку дуже повільно, а потім все швидше зростають. При резонансній частоті вони зростають в десятки і навіть сотні разів. Якщо далі збільшувати частоту, сила струму і на­пруга починають спочатку швидко, а потім все повільніше зменшуватися і при досить великій частоті майже дорів­нюють нулю.

Електричний резонанс в колі можна одержати не тільки зміною частоти генератора, а й при заданій частоті, змінюючи або індуктивність котушки, або ємність кон­денсатора.

Досі ми розглядали кола змінного струму, в яких рези­стор, конденсатор і котушка з'єднані послідовно. Розгля­немо тепер коло з увімкнутими паралельно котушкою і конденсатором (мал. 38). Припустимо, що активний опір обох віток розгалуження настільки малий, що ним можна нехтувати. До клем кола а і b прикладена змінна синусої­дальна напруга. Треба визначити коливан­ня сили повного струму в колі (тобто сили струму, яку вимірює амперметр А, увімкнутий до підвідних провід­ників).

Напруга на паралельно з'єднаних вітках розгалуження однакова і дорівнює прикладеній напрузі . Миттєве значення сили струму в нерозгалуженій частині кола /(*) дорівнює алгебраїчній сумі сил струмів в паралельних вітках розгалуження;

Оскільки сила струму у вітці розга­луження, яка містить конденсатор, ви­переджає напругу на, а сила струму через котушку відстає від напруги на -г-л, то векторна діаграма для цього

Таким чином, сила струму в нерозгалуженій частині кола дорівнює:

кола має вигляд, показаний на малюн­ку 39. Векторна діаграма дає можливість записати вирази для миттєвих значень сили струму в обох вітках розгалу­ження :

Коли ємнісний і індуктивний опори однакові, тобто

(22.2)

то сила струму в нерозгалуженій частині кола дорівнює нулю, хоча в контурі, який складається з L і С, сила струму може бути дуже великою. Це явище називається резонан­сом струмів. Для резонансної частоти з рівності (22.2) дістанемо таке саме значення, що й при резонансі напруг.

Для струму резонансної частотиконтур з малим

активним опором R становить дужевеликий опір, тим біль­ший, чим менше R (приопір контуру Z прагне до нескінченності).

Резонанс струмів (резонанс напруг) широко використо­вується в техніці. Для прикладу розглянемо будову і прин­цип дії найпростішого резонансного підсилювача (мал. 40). В анодне коло підсилювача вмикають коливальний кон­тур, настроєний на частоту сигналу, який треба підсилити. Для резонансної частоти (точніше, для вузької смуги частот) контур становить великий опір і коливання анод-

ного струму лампи викликають на його кінцях появу змінної напруги. Для цієї частоти резонансний підси­лювач діє так само, як і звичайний підсилювач на резисторах, причому роль анодного опору відіграє коли­вальний контур. Для всіх інших ча­стот, які помітно відрізняються від резонансної, контур є практично ко­ротким замиканням анодного кола, і тому підсилення напруги не відбу­вається.

Ви вже знаєте, що під час резонансу струмів силу струму в обох вітках розгалуження кола можна зробити набагато більшою, ніж у підвідних проводах. Цю обставину викори­стовують в індукційних печах, в яких нагрівання металів здійснюється вихровими струмами. Для цього паралельно нагрівальній котушці К вмикають конденсатор С і доби­рають його ємність так, щоб одержати на частоті генера­тора, який живить піч, резонанс струмів. Тоді через під­відні проводи і генератор проходить порівняно невеликий струм, сила якого дорівнює різниці І_к—І_с і яку можна зробити в десятки разів меншою, ніж силу струму І_к в на­грівальній котушці.

З викладеного вище випливає, що електричний резо­нанс в колі можливий лише в тому випадку, коли воно містить одночасно і ємність, і індуктивність. В колах, які містять лише ємності, або лише індуктивності, резонанс не спостерігається.

Явище резонансу в електричних колах відіграє дуже велику роль в електротехніці і радіотехніці. З деякими важливими галузями його застосування ми далі ознайо­мимося.

? 1. У чому суть електричного резонансу? 2. Чому дорівнює амплі­туда сили струму під час резонансу? 3. Від яких параметрів кола зале­жить резонансна частота контуру? 4. Чи може амплітуда напруги на конденсаторі чи котушці індуктивності під час резонансу перевищити амплітуду напруги, прикладеної до кола? 5. Чи існує зсув фаз між коли­ваннями сили струму і напруги під час резонансу? Чому? в. Чи може спостерігатися резонанс у колі, яке містить лише активний і ємнісний, або активний та індуктивний опори?