3. Уравнение Бернулли для элементарной струйки идеальной жидкости.

В виду сложности уравнений (2.6) их общее решение до сих пор не получено. Если рассмотреть аналогичные уравнения для движения вязкой жидкости, ещё более сложные чем (2.6) то, как показано в дополнительной части к этой главе, даже простейшие частные решения, далёкие от практических запросов получаются весьма не просто. Для получения общего интеграла уравнений (2.6) пригодного в дальнейшем для инженерных приложений каждый член в их правой и левой частях умножается на малый элемент перемещения вдоль линии тока. При этом все полученные произведения приобретают смысл или энергии или работы внешних сил. Затем три полученных скалярных уравнения складываются, интегрируются вдоль линии тока и получается интеграл Бернулли, с помощью которого возможно определить механическую энергию потока в любом сечении элементарной струйки.

Таким образом, исходя из уравнений, выражающих закон сохранения количества движения возможно выяснить, какой вид имеет закон сохранения энергии при движении жидкости. В результате отпадает необходимость точно учитывать все граничные условия и главной характеристикой в рассматриваемом сечении является механическая энергия.

Рассмотрим элементарную струйку идеальной жидкости, находящуюся в установившемся движении. При установившемся движении частные производные скорости по времени равны нулю, т.е.

(3.1)

и линии тока совпадают с траекториями частиц и, следовательно, с элементарными струйками. Поэтому проекции перемещения равны произведениям соответствующих проекций скорости и времени dt,

(3.2)

Каждое из уравнений (2.7) умножим на соответствующее перемещение

dx,dy,dz и сложим отдельно левые и правые части; в результате получим:

(3.3)

Е

(3.4)

сли на жидкость действует только сила тяжести, ускорение которой равно g, то при выбранных направлениях координатных осей

т

(3.5)

огда

Сумма в скобках в левой части (3.3) в условиях установившегося движения (т.е. когда давление р не зависит от времени, а зависит только от координат т.е. р = f(x,y,z,)), представляет собой полный дифференциал давления.

(3.6)

Правую часть (3.3) с учётом (3.2) преобразуем так

(3.7)

Далее выполним такие преобразования

(3.8)

(так как, например:), т. е. дифференциал функции равен производной этой функции, умноженный на дифференциал аргумента.

Учитывая, что дифференциал суммы равен сумме дифференциалов, правую часть (3.8) преобразуем так

(3.9)

где u - скорость элементарной струйки, одинаковая по ее сечению.

Подставив в (3.3) результаты всех преобразований из (3.5),(3.6),(3.9) и разделив на ускорение свободного падения g получим выражение:

(3.10)

В данном случае исходными являлись уравнения Эйлера и размерность их (до деления на ρdxdydz – массу рассматриваемой частицы) была размерностью силы, а при умножении на перемещение могла бы стать размерностью энергии. Фактически каждый член (3.10) получен путём деления соответствующего вида механической энергии на ρdxdydz – вес рассматриваемой частицы. Первоначально имелось в виду движение частицы жидкости, поэтому заключаем, что каждые слагаемые в (3.10) представляет механическую энергию частицы жидкости, отнесённую к её весу, т.е. энергию, делённую на её вес – так называемую удельную энергию.

После формального интегрирования (3.10) получим

(3.11)

Если в (3.11) принять ρ=const, имея в виду капельную несжимаемую жидкость, то получим уравнение (3.11) в таком виде

(3.12)

Уравнение (3.12) называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Уравнение (3.10) справедливо также в том случае, когда рассматриваются два близлежащих (на расстоянии dl) сечения, все значения величин, в которых мало отличаются друг от друга. Следует напомнить, что уравнения Эйлера выведены на основе второго закона Ньютона (уравнение движения), а интегралом этих уравнений движения является уравнение Бернулли, выражающее закон сохранения и превращения энергии.

Использование уравнения Бернулли основано на написании этого уравнения для двух специально выбранных сечений 1-1 и 2-2

(3.13)

,

в одном из которых все три слагаемых известны. Тогда в другом сечении по двум заданным или независимо определенным слагаемым находится третье - т.е. одна из величин z,p или u.

Задача 3.1. Сопло фонтана имеет форму усеченного конуса, сужающегося вверх. Диаметры сечений такие: нижнего D = 50мм, верхнего d = 10мм; высота сопла от нижнего до верхнего сечения h = 0,5м. Определить расход воды, подаваемый фонтаном и давление в нижнем сечении, если вода поднимается на высоту Н = 8м. Сопротивление воздуха и сопротивление в потоке не учитывать.

Решение: Очевидно, что в наивысшей точке подъема на высоте Н вся кинетическая энергия струи перейдет в потенциальную, поэтому

где u₂ - скорость истечения воды из сопла.

Зная площадь выходного (узкого) сечения сопла S₂, найдем искомый раcход

Из уравнения неразрывности

найдем скорость в нижнем (широком) сечении

.

Уравнение Бернулли, записанное для двух сечений (широкого и узкого сечений сопла) будет иметь вид

Неизвестное давление определяется из последнего уравнения.

Задача 3.2 Поток переходит из широкого сечения трубы в узкое. Определить, в каком сечении, в узком или широком, давление больше. Жидкость считать идеальной.

Решение. Представим трубу

горизонтальной, выберем два сечения 1-1 и 2-2 и плоскость отсчета 0-0 совпадающую с осью трубы. Уравнение Бернулли для данного случая(z₁=z₂=0) преобразуется так

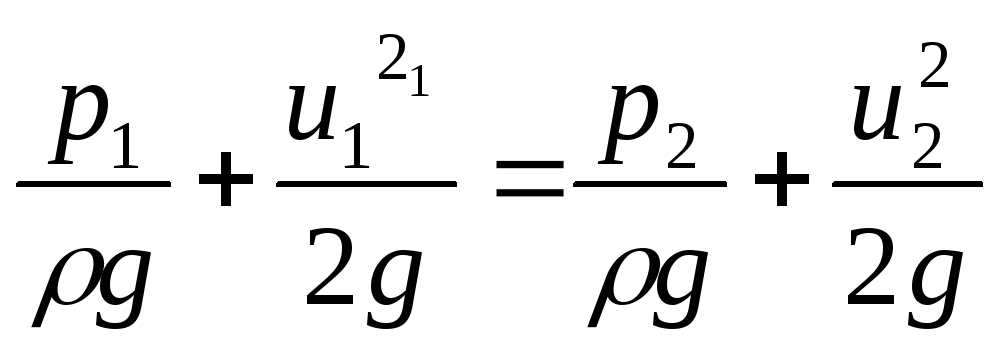
или

Очевидно, что > (из уравнения неразрывности) и правая часть >0, следовательно, и левая часть последнего соотношения положительна.

Поэтому

_>.

Этот результат можно получить более простым путем. Считая жидкость идеальной, мы уверены, что происходит лишь превращение одного вида механической энергии в другой (без перехода в тепло). Кинетическая энергия жидкости (проходящей за единицу времени через сечение 1) при переходе в узкое сечение возрастает (при Q = const). Следовательно - потенциальная энергия убывает и _>

Задача 3.3. Вывести уравнение Бернулли для случая изотермического движения газа (без учета потерь).

Решение. Для решения задачи применим общее уравнение (3.10); проинтегрируем его в пределах двух сечений и учтем, что для изотермического процесса

Подставляя выражение для плотности в интеграл, содержащий давление

получим окончательно: