Дополнительная часть.

Задача Д.1.1. Записать систему дифференциальных уравнений равновесия в векторной форме. Как будет выглядеть уравнение равновесия для любого направления .

Решение Умножим дифференциальные уравнения системы равновесия (4.7) на орты и сложим соответственно левые и правые части. В результате получим

grad p –  = 0,

где - вектор ускорения внешней силы.

Умножим скалярно последнее уравнение на орт любого направления получаем уравнение равновесия на любое направление

Д.2. Потенциал силы. Поверхность уровня.

Так как в уравнении (4.2)

dр =  (X dx + Y dy + Z dz)

dр есть полный дифференциал, то выражение в скобках правой части также будет полным дифференциалом некоторой функции координат, т.е.

X dx + Y dy + Z dz = d U (x, y, z)

Здесь величины X, Y, Z, т.е. проекции ускорения объемной силы можно рассматривать как проекции самой объемной силы, отнесенной к единице массы данной жидкости. Поэтому функция U (x, y, z) является потенциалом сил. Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.

Следовательно

(Д.2.1)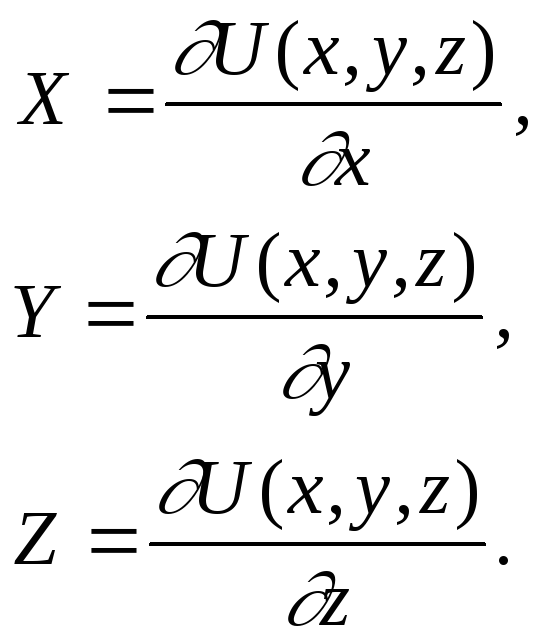

Поверхность уровня.

Поверхностью уровня называется такая поверхность, все точки которой имеют одно и то же значение рассматриваемой величины.

Например, поверхность равной температуры (изотермическая поверхность), поверхность равного давления (свободная поверхность жидкости) и т.д.

Так как во всех точках поверхности уровня гидростатическое давление одинаковое, т.е. р = соnst, dр = 0 и из (5.2) следует

 (X dx + Y dy + Z dz) = 0.

Т

(Д.2.2)

ак как плотность   0, то

X dx + Y dy + Z dz = 0,

где X, Y, Z – функции координат.

Уравнение (Д.2.2) представляет собой дифференциальное уравнение поверхности, для которой р = const, т.е. уравнение поверхности равного давления.

Задача Д.2.1. Построить эпюру Задача Д.2.2. Построить эпюры

давления на стенку при двустороннем избыточного и абсолютного

давлении воды, рис. Д.2.1. давлений на наклонную стенку бака,

в который налиты жидкости

различных плотностей, рис Д.2.2

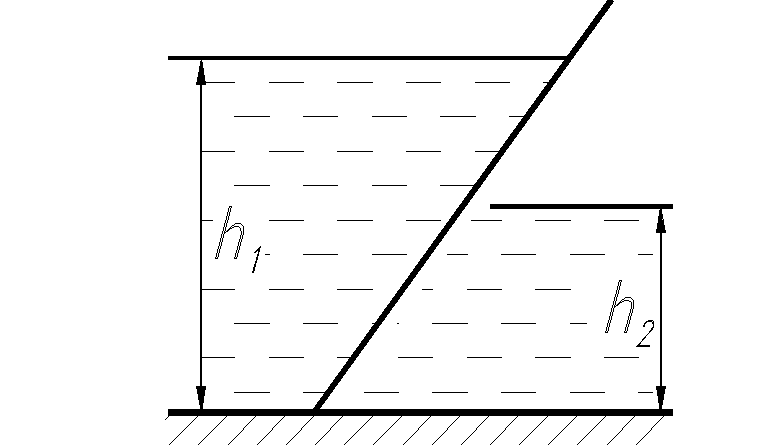
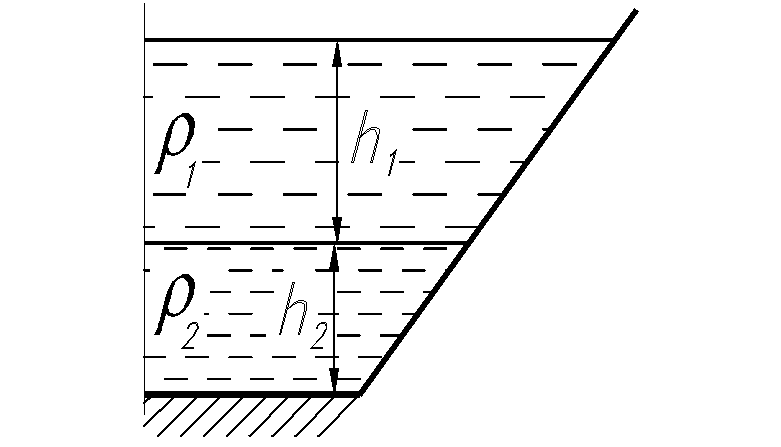
Рис. Д.2.1. Рис. Д.2.2

Д.3. Центр давления.

Центром давления называется точка приложения силы давления жидкости на заданную площадку.

Центр давления, как любая точка, определяется в пространстве тремя координатами, а на плоскости – двумя. В данном случае необходимо определить только глубину погружения, центра давления под свободной поверхностью; обозначим координату центра давления z_d.

Положение центра давления, возможно, определить по теореме о моментах, согласно которой момент равнодействующей силы равен алгебраической сумме моментов составляющих сил.

Если F- равнодействующая сила гидростатического давления, определяются по формуле (11,9), то z_d может определена из равенства:

При решении этой задачи необходимо иметь в виду, что интеграл

представляет собой момент инерции площади S относительно оси Ох.

Из теоретической механики известно, что момент инерции некоторой площади S относительно заданной оси равен моменту инерции этой площади относительно оси, проходящей через центр тяжести площади и параллельной данной оси, плюс произведение площади S на квадрат расстояния между осями.

Задача Д.3.1. Найти глубину погружения центра давления и доказать, что центр давления лежит всегда ниже центра тяжести данной площади.

Задача Д.4.1. В сосуд налиты две несмешивающиеся между собой жидкости с плотностями ₂ > ₁. Определить плотность  сплошного шара, плавающего в сосуде при полном погружении, причем его центр лежит в плоскости раздела жидкостей, рис. Д.4.2.

Рис. Д.4.2.