2.Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера).

Поставим задачу получить дифференциальные уравнения, которые описывали бы движение идеальной жидкости. По аналогии с механикой материальной точки выполним следующие действия :

• Рассмотрим в потоке бесконечно малую жидкую частицу ;

• Определим все действующие на эту частицу силы и их результирующую;

• Составим для частицы как для материальной точки уравнение движения (второй закон Ньютона);

• Перейдём в полученных уравнениях к пределу, стягивая объём к некоторой его внутренней точке;

В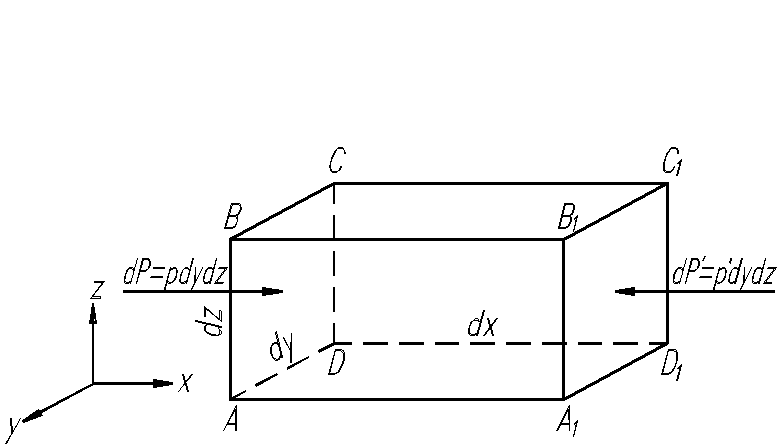 потоке идеальной жидкости выделим элементарную массу (движущуюся частицу) в форме параллелепипеда и применим к этому объему текущей жидкости второй закон Ньютона: равнодействующая всех внешних сил , действующих на данное тело, равна массе тела , умноженной на ускорение , с которым движется это тело, т.е.

(2.1)

Есть параллелепипед с ребрами dx, dy и dz, рис.2.1и проекций сил действующих на него будут иметь вид

(2.2)

Рис. 2.1

Т

(2.3)

ак как все оси равноправны, то рассмотрим в дальнейшем только первое из уравнений (2.2) (в проекции на ось Ох). Масса параллелепипеда равна

Ускорение частицы (параллелепипеда) вдоль оси Ох равно (Кинематика):

(2.4)

Таким образом правая часть первого из уравнений (2.2) имеет вид:

(2.5)

Рассмотрим теперь результирующую внешних сил в левой части первого уравнения (2.2).

Течение невязкой жидкости характеризуется отсутствием сил внутреннего трения (касательных напряжений). Поэтому силы гидродинамического давления в таком потоке, как и в случае равновесия, имеют только нормальную составляющую.

В курсах гидромеханики доказывается, что и при движении идеальной жидкости величина гидродинамического давления не зависит от ориентации площадки, на которую оно действует.

Таким образом, внешними силами являются поверхностные силы (силы давления жидкости, окружающей выделенную элементарную массу, на ее боковые грани) и силы объемные ( или массовые).

В соответствии с рис. 2.1. найдем: проекция силы давления на боковую грань АВСД равна

проекция силы давления на боковую грань A'B'C' Д' равна

Остальные поверхностные силы в проекциях на ось Оx дают ноль.

Давление р' найдем, разложив р в ряд Тейлора и учитывая только члены первого порядка

Сила войдет в уравнение со знаком минус, т.к. ее направление противоположно силе . Окончательно

Проекция объемной силы определится так

^,

где - проекция ускорения объемной силы, ρ- плотность жидкости, dx dy dz - объем параллелепипеда.

Так как иных сил нет, то проекция равнодействующей равна

Уравнение (2.2) получим в таком виде

В последнем уравнении левую и правую части можно разделить на

ρdxdydz, т.е. каждое слагаемое отнесём к массе частицы. В результате получим

Аналогично можно составить выражения для проекций уравнения движения на другие оси и система уравнений будет иметь вид.

(2.6)

Или, в краткой записи:

(2.7)

Эта система дифференциальных уравнений( полученная Л. Эйлером в 1775г.) на самом деле представляет три проекции на осях декартовой системы координат одного уравнения движения идеальной жидкости

где - вектор ускорения внешних массовых сил, grad p – градиент давления.

Система (2.7) справедлива как для жидкостей, так и для газов; в ней пять неизвестных - составляющие скорости давление р и плотность ρ . Поэтому для решения (2.6) или (2.7) требуются дополнительно еще два уравнения ; ими являются уравнение неразрывности и характеристическое уравнение (связывающее давление, плотность и температуру).

Сами по себе полученные дифференциальные уравнения весьма общие и для решения их необходимо задать те конкретные условия, в которых происходит течение, т.е. задать границы (геометрию границ и условия на них).

Очевидным условием является то, что через границу потока жидкость не протекает; тогда нормальная составляющая скорости u_n (направленная под прямым углом к границе) равна нулю т.е.

u_n=0, во всех точках граничной поверхности.

Идеальная жидкость не имеет вязкости, поэтому её частицы могут скользить по поверхности и касательная составляющая скорости u_τ (проекция скорости на направление вдоль границы) в точках поверхности границы не равна нулю т.е.

.

При течении реальной, т.е. вязкой жидкости её частицы прилипают к граничной поверхности и поэтому в любой точке границы обе составляющие равны нулю

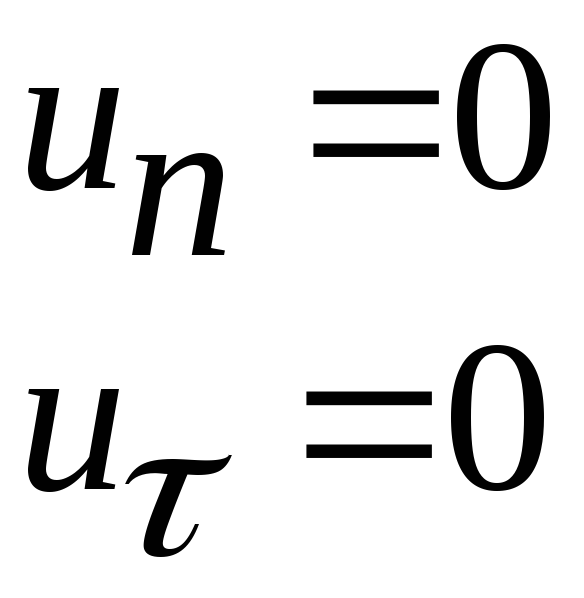
Уравнения (2.6) являются следствием закона сохранения количества движения для идеальной жидкости, находящейся в движении, а физический смысл этих уравнений в том, что они выражают связь между всеми внешними силами и параметрами движения потока в точке.

Задача 2.1. Записать уравнения (2.6) для случая плоского установившегося (стационарного) течения; записать(2.6) для случая одномерного установившегося течения вдоль любой оси.