Гидравлические сопротивления.

1. Ламинарный и турбулентный режимы движения жидкости.

Ламинарный режим обычно характеризуется параллельно движущимися слоями, или струйками. Его можно рассматривать как движение отдельных слоев жидкости, происходящее без перемешивания.

При турбулентном режиме отдельные слои перемешиваются между собой и частицы движутся хаотично, по изменяющимся во времени траекториям. Качественные различия режимов можно наблюдать, пуская струйки окрашенной жидкости в поток, т.е. делая отдельные струйки видимыми.

Основными факторами, определяющими характер режима в круглой трубе являются: средняя скоростьV, диаметр d, кинематический коэффициент вязкости . Для характеристики режима движения жидкости введен безразмерный параметр Re, учитывающий влияние перечисленных факторов, называемый числом (критерием) Рейнольдса.

(1.1)

В таком виде число Re применимо для движения в трубе. Представим, что имеем возможность изменять скорость течения в трубе, например краном. В начале, при открытии крана режим движения ламинарный а затем при увеличении скорости он перейдёт в турбулентный. Число Re, при котором произошел этот переход (называется верхним критическим) зависит от многих случайных факторов и не является характерным. Если, имея в трубе развитый турбулентный режим, постепенно закрывать кран (уменьшая тем самым скорость), то при некотором числе Re установится ламинарный режим. Это число Рейнольдса является характерным и называется нижним критическим – Re_{кр н.}.

В настоящее время для характеристики режима движения принято считать, что границей служит некоторое критическое число Рейнольдса Re_кр=2300. Полагают, что при Re<2300 режим ламинарный, а при Re>2300 режим турбулентный. В трубопроводах систем снабжения и водоотведения, систем отопления, вентиляции и газоснабжения, в открытых каналах и реках движение является турбулентным. Ламинарный режим встречается значительно реже; он имеет место в тонких ламинарных трубках, при движении воды (фильтрации) в порах грунта и при движении очень вязких жидкостей (масло, нефть и т.д.).

Задача 1.1. Диаметр круглой трубы изменяется от d₁ до d₂>d₁; в каком сечении – узком или широком число Re больше?

Решение. I. Способ. Числа Re для сечений 1 и 2 имеют вид: и . Отношение их будет равно: (1.2)

Расход в узой и широкой частях трубы одинаковый; уравнение неразрывности даёт V₁S₁=V₂S₂ или V₁/V₂=S₂/S₁. Для круглой трубы площадь сечения равна S=πd²/4, отношение скоростей из уравнения неразрывности выразится так V₁/V₂=d₂²/d₁². Подставляя V₁/V₂ в (1.2) получим . Так как отношение числа Re обратно пропорционально отношению диаметров, то в узком сечении число Re больше.

2. Способ. Если выразить среднюю скорость, входящую в число Re через расход, то можем записать (имея в виду, что )

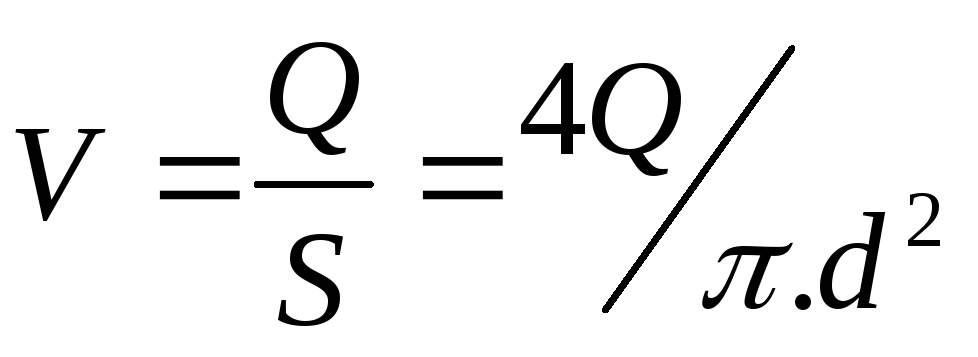Так как расход в любом сечении одинаковый, то число Re зависит от диаметра d, стоящего в знаменателе; следовательно, в узком сечении число Re больше, чем в широком.