Formules

1) Le volume d’une boule

2) L’aire d’une sphère

Exercices

113) Un cylindre a une hauteur de 60 cm et un diamètre de 18 cm. Calcule son volume V au cm³ près.

1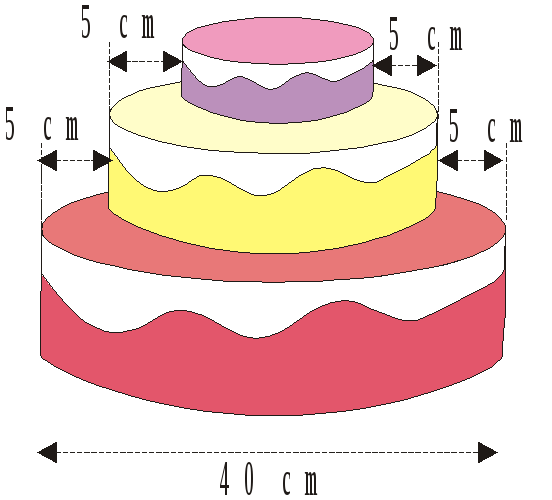14) Calcule le volume d’un cylindre de 2,5 m de haut et de rayon 55 cm.

115) Calcule le volume de la pièce montée

sachant que chaque couche est cylindrique

et mesure 6 cm de haut.

116) Un tube en acier a la forme d’un cylindre creux

de longueur 1,20 m , de diamètre intérieur 32 mm et

de diamètre extérieur 40 mm. Calcule, à 0,01 cm³ près,

le volume d’acier nécessaire à la réalisation du tube.

117) Calcule l’aire latérale du cylindre ci-dessous de hauteur 5 cm et de rayon 3 cm (à 0,1 cm² près).

118) Le cylindre d’un rouleau compresseur a un rayon de 60 cm et une largeur de 168 cm. Quelle est l’aire aplanie en un tour (au cm² près) ?

119) Le cylindre de révolution a pour hauteur 4,5cm et son cercle de base a pour rayon 1cm. a) Quelles sont la nature et les dimensions de la section du cylindre par un plan contenant son axe de révolution? b) Quelles sont la nature et les dimensions de la section du cylindre par un plan perpendiculaire à son axe de révolution?

120) Le cylindre de révolution d'axe (OO') a pour hauteur 8cm et pour rayon 6cm. Il a été coupé par un plan parallèle a son axe de révolution passant par le point H tel que OH = 4cm. a) Calculez la mesure de l'angle AOH arrondie au degré. b) Déduisez-en la mesure de l'angle AOB arrondie au degré.

121) L’unité est le centimètre. On considère le cylindre C ci-contre, dont la base a pour rayon R = 5 et dont la hauteur est h = 8. Les points M et N sont sur la circonférence du disque formant la base supérieure, et MON est un angle droit.

1. Calculer la longueur MN, puis la mesure de l’angle OO′M au degré près.

2. Tracer en vraie grandeur :

a) la section de ce cylindre par le plan passant par P et parallèle à la base.

b) la section de ce cylindre par le plan passant par M et N, et parallèle à l’axe du cylindre.

122) On considère un cône de révolution de hauteur SO = 8 cm et dont la base est un disque de 3 cm de rayon. A et B sont deux points diamétralement opposés sur la circonférence du disque de base.

1. De quelle nature est le triangle SAB ? Calculer la mesure au degré près de l’angle SAB.

2. Calculer la valeur exacte du volume de ce cône.

3. Soit O′ le milieu de [SO]. On considère la section du cône par le plan parallèle à la base et passant par ce point O′.

a) Dessiner en vraie grandeur cette section.

b) Le petit cône est une réduction du grand cône ; donner le rapport de cette réduction, et en déduire la valeur exacte du volume du petit cône.

123) Un cône de révolution a pour génératrice 5,3cm et pour rayon de base 2,8cm. Calculer le volume de ce cône. Calculer l'aire latérale de ce cône.

124) Un cône de révolution a pour génératrice 9cm et pour rayon de base 2,8cm. Calculer l'angle du développement de la surface latérale de ce cône. Calculer l'aire latérale de ce cône.

125) Le développement de la surface latérale d'un cône de révolution est un secteur circulaire de rayon 9 cm et d'angle 112°.

a) Déterminer le périmètre de base de ce cône et son rayon de base.

b) Déterminer l'aire latérale et l'aire totale de ce cône.

126)  Calculer le volume d'un cône de révolution si sa hauteur mesure 12 cm et son angle au sommet ASB mesure 90°. (On donnera une valeur approchée de la réponse à 0,1 cm³ près).

127) La section de la sphère S de centre O et de rayon 4 cm par le plan P perpendiculaire а (OA) est le cercle de centre A et de rayon AB. Sachant que la distance de O à P est OA = 3 cm calculer AB.

128) On réalise la section d’un cône de hauteur SO = 8 cm par un plan parallèle à la base passant par le point O’ tel que SO’ = 2 cm. On donne le volume du grand cône V =153,6 cm³ et l’aire de la base A = 57,6 cm². Calculer le volume v du petit cône et l’aire a de sa base.

129) Deux récipients ont le même volume. L'un a la forme d'un cylindre de hauteur 10 cm et de rayon de base 6 cm. L'autre a la forme d'un cône de rayon de base 6 cm. Quel est le volume du récipient cylindrique? Quelle est la hauteur du récipient conique?

130) a) Quel est le rayon d’une sphère dont l’aire est égale à 200 cm² ? Quel est le volume que peut contenir cette sphère ?

b) Puis-je verser le contenu (liquide) d’une sphère de 5 cm de rayon dans un cylindre creux de 5 cm de rayon et de 7 cm de hauteur ?

c) Un verre parallélépipédique (longueur 3cm, largeur 3 cm, hauteur 8 cm) contient 63 ml d’eau. Quelle est la hauteur d’eau dans ce récipient ? On y plonge deux glaçons sphériques de 2 cm de diamètre. L’eau va-t-elle déborder du verre ?

131) Calculer l’aire et le volume de chacun des solides suivants :

132) Calculer le volume de chacun des solides suivants :

133) Ici on voit que le plan vient sectionner la sphère de centre O de rayon R selon un cercle.

1. Calculer le rayon de ce cercle de section :

a) dans le cas où OH = 12 cm et R = 15 cm,

b) dans le cas où NH = 12 cm et R = 10 cm,

c) dans le cas où R = 5 cm et HOM = 26⁰,

2. Quelle est la distance du plan de section au centre de la sphère :

a) dans le cas où r = 5 cm et R = 7 cm,

b) dans le cas où R = 12 cm et HOM = 35⁰