2. 2 Pyramides

Mots à retenir

le cercle circonscrit (описанная окружность)

le cercle inscrit (вписанная окружность)

le pied de la hauteur (основание высоты) l’apothème (апофема)

le tronc de pyramide (усечённая пирамида)

Définitions

1) Une pyramide est un solide dont une face est un polygone (appelé la base de la pyramide) et les faces latérales des triangles qui ont un sommet commun s’appelle sommet de la pyramide.

3) Une pyramide dont la base est un triangle est appelée le tétraèdre.

4) La hauteur d'une pyramide est le segment issu du sommet et perpendiculaire à la base.

5) Les arêtes latérales sont les segments joignant les sommets de la base au sommet de la pyramide.

Exemple 

2) Une pyramide est régulière lorsque sa base est un polygone régulier et si le pied de la hauteur de la pyramide est le centre de ce polygone.

Propriétés Dans une pyramide régulière

a) Les faces latérales sont des triangles isocèles semblables.

b) Les arêtes latérales ont la même longueur.

c) Le pied de la hauteur d’une pyramide régulière est le centre du cercle circonscrit à sa base.

Formules

1) l’aire totale est la somme des aires de toutes les faces (base comprise).

2) le volume est le produit de l’aire de la base et de la hauteur divisé par 3.

Exercices

94) Calculer le volume et l’aire totale des pyramides suivantes :

a) b)

95) SEFGH est une pyramide à base rectangulaire.

a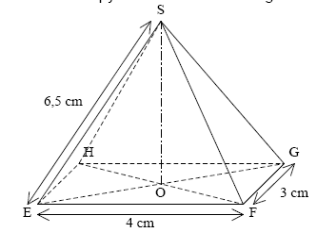) Indiquer les longueurs des arêtes [GH] et [HE].

b) Calculer la longueur EG.

c) Calculer la longueur SO.

96) SABCD est une pyramide régulière à base carrée. La diagonale de la base mesure 5cm et l’arête latérale mesure 7 cm. Calculer la hauteur de la pyramide. Arrondir au mm.

97) Une pyramide à base rectangulaire de 4 sur 6 a pour volume 60 cm³. Quelle est sa hauteur ?

98) Une pyramide à base carrée a pour volume 243 cm³ ; sa hauteur mesure 9 cm, quelle est la mesure du côté du carré de base ?

99) On considère la pyramide ABCD : de hauteur [AD] telle que AD = 5 cm ; de base ABC telle que :

AB = 4,8 cm ; BC = 3,6 cm ; CA = 6 cm.

1) Démontrer que le triangle ABC est rectangle en B.

2) Calculer le volume de cette pyramide.

3) On désire fabriquer de telles pyramides en plâtre. Combien peut-on en obtenir avec 1 dm³ de plâtre ?

100) SABCD est une pyramide régulière à base carrée, de sommet S et de hauteur [SO]. AB = 4 cm et SO = 5 cm. Dessiner un patron de cette pyramide. Calculer le volume de cette pyramide.

101) Une tente de forme pyramidale régulière, à base carrée,

a les dimensions indiquées sur la figure ci-contre. Quelle

est la quantité de toile nécessaire à sa fabrication (plancher

compris) ?

102) ABCDE est une pyramide dont la base ABCD est

un trapèze rectangle de bases [AB] et [CD] avec

(AD)(AB). La droite (EC) est orthogonale au plan (ABCD).

On a AB = 5, DC = 7, AD = 3 et EC = 4.

1) Calculer le volume de la pyramide ABCDE.

2) I, J et K sont les milieux respectifs de [DE], [AE] et [BE].

a) Montrer que les plans (IJK) et (ABC) sont parallèles.

b) Tracer la section de la pyramide ABCDE par le plan (IJK).

103) La pyramide de Khéops ou Grande Pyramide, édifiée à Guizeh en Egypte, est régulière à base carrée. Sa hauteur, qui est encore actuellement de 138 m, devait être à l'origine de 146,6 m. La longueur de la base est de 230 m. Notons S le sommet de la pyramide, ABCD le carré de base et O le centre de ABCD, c'est-à-dire l'intersection des diagonales (AC) et (BD).

1) Que dire des droites (SO) et (AC) ?

2) Calculer la valeur exacte de la demi-diagonale [OB].

3) Calculer la valeur exacte de SA et donner une valeur approchée à 1 m près. (on prendra SO=146,6 m)

4) L'apothème de la pyramide est la distance du sommet S à l'un quelconque des côtés de la base. Notons H le pied de la hauteur issue de S du triangle SAB.

a) Pourquoi H est-il le milieu de [AB] ? b) Donner la valeur exacte de SH et une valeur approchée à 1 m près. c) Calculer le volume de la pyramide et en donner une valeur approchée à 1m³ près.

104) SABCD est une pyramide à base carrée, de hauteur [SA] tel que : AB = 9cm et AS = 12 cm. 1) Calculer le volume de cette pyramide. 2) on appelle E le point de [SA] tel que : SE= 3 cm. La parallèle à la droite (AB) passant par le point E coupe [SB] en F. Calculer la longueur EF. 3) La pyramide SEFGH a pour base le carré EFGH et pour hauteur [SE]. Calculer son volume. 4) le solide ABCDEFGH s'appelle un tronc de pyramide. Calculer le volume de ce solide.

105) ABCDEFGH est un cube d’arête 6 cm.

a) Calculer la longueur du segment [BD].

b) Calculer la longueur du segment [HB]

c) Dans le triangle ABH, calculer la mesure à un degré près de l’angle AHB.

d) Calculer le volume de la pyramide de sommet H et de base DAB.

106) La pyramide du Louvre est une pyramide régulière à base carrée de côté 34 m et de hauteur 21 m. Calcule le volume de cette pyramide.

107) La pyramide SABCD a pour base le rectangle ABCD de côtés AB=7cm et BC=4cm, de centre le point H. La hauteur SH de la pyramide mesure 5cm. K est le milieu de [BC] et L est le milieu de [AB]. Dessiner la base ABCD, placer les points H, K et L, calculer HL, HK et HB. Dessiner une vue en perspective cavalière de la pyramide. Calculer son volume. Calculer l'aire totale de la pyramide SABCD.

108) SABCD est une pyramide régulière (donc les arêtes SA, SB, SC et SD ont la même longueur). Sa base est le carré ABCD de côté 6cm. H est le point d’intersection des diagonales AC et BD. SH est la hauteur de cette pyramide et . M est le milieu du segment [BC].

1) Calculer le volume de cette pyramide.

2) Pour dessiner le développement de la pyramide SABCD :

a) Au centre d’une feuille, dessiner le carré ABCD, placer les points M et H.

En étudiant le triangle BHC, expliquer pourquoi.

b) Dire pourquoi SHM est un triangle rectangle. Dessiner le triangle SHM.

Quelle est la nature de la face SBC ? Sur le développement commencé en a), dessiner la face SBC et les autres faces de la pyramide SABCD.

3) Dans le triangle SHM, Calculer SM. Calculer l’angle à 0,1° près. Calculer l’aire du triangle SBC.

109) SABC est une pyramide dont la base ABC est un triangle rectangle isocèle en B. L’arête [SA] est la hauteur de cette pyramide.

a) Dans le triangle SAB, calculer la longueur SB de l’hypoténuse.

b) Dans le triangle rectangle ABC, calculer la longueur AC : arrondir au mm.

c)Calculer la longueur SC : arrondir au mm.

110) On considère une pyramide de hauteur SB = 10 cm et dont la base est un triangle ABC tel que AB = 4,5 cm, BC = 7,5 cm et AC = 6 cm.

1. Montrer que ABC est un triangle rectangle ; calculer son aire.

2. Calculer la valeur exacte du volume de cette pyramide.

3. Soit B′ le point de l’arête [SB] tel que SB = 8 cm. On coupe la pyramide par un plan parallèle à la base et passant par ce point B. On obtient les points A′ sur [SA] et C′sur [SC].

a) Dessiner en vraie grandeur le triangle A′B′C′, en donnant ses dimensions précises. De quelle nature est ce triangle ? Quelle est son aire ?

b) La pyramide SA′B′C′ est une réduction de la pyramide SABC ; quel est le rapport de cette réduction ?

c) Calculer le volume de la pyramide SA′B′C′.On donnera la valeur exacte puis la valeur arrondie au mm³.

111) SABC est un tétraèdre dont la base est un triangle rectangle et isocèle en C. La hauteur est l'arête [SC]. De plus SC = 3 cm, CA = CB = 4 cm.

a) Calculer le volume de cette pyramide. b) Calculer la longueur SA.

c) Calculer l'angle à 1 degré prés CAS.

112) ABCDE est une pyramide régulière dont toutes les faces latérales sont des triangles équilatéraux de côté 4 cm et la base un carré BCDE de centre O.

a) Utiliser le triangle ABO rectangle en O pour calculer la hauteur exacte AO de la pyramide.

b) Calculer la valeur exacte de son aire latérale, c’est-à-dire de la somme des aires des faces autres que la base.