П.Геворкян. Сборник задач по высшей математике

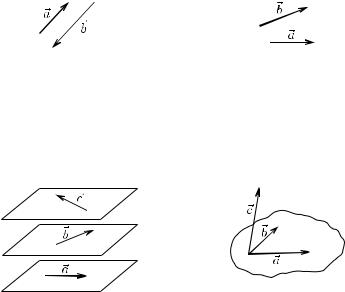
§ 3.2. Коллинеарные и компланарные векторы

Два вектора и называются коллинеарными, если они лежат на

одной прямой или на параллельных прямых (рис. 3.3). В противном случае они называются неколлинеарными (рис. 3.4).

Рис. 3.3. Коллинеарные векторы Рис. 3.4. Неколлинеарные векторы

Три вектора , и называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях (рис. 3.5).

В противном случае векторы , и называются некомпланарными (рис. 3.6).

Рис. 3.5. Компланарные векторы Рис. 3.6. Некомпланарные векторы

3.12. Доказать, что ненулевые векторы и коллинеарны

тогда и только тогда, когда = , где — однозначно опреде-

ленное число.

3.13. Доказать, что ненулевые векторы , и компланарны

тогда и только тогда, когда один из них линейно выражается через другие.

3.14. Доказать, что любой вектор плоскости представля-

ется, причем единственным образом, в виде линейной комбинации любых двух наперед заданных неколлинеарных векторов 1 и 2:

= 1 1 + 2 2.

3.15. Доказать, что любой вектор пространства представ-

ляется, причем единственным образом, в виде линейной комбинации любых трех наперед заданных некомпланарных векторов

1, 2 и 3:

= 1 1 + 2 2 + 3 3.

3.19. Известны разложения векторов и по трем неком-

планарным векторам , , :

= 1 + 2 + 3 ,

= 1 + 2 + 3 .

Какая зависимость должна существовать между коэффициентами этих разложений, если

§ 3.3. Прямоугольная система координат

1 . Прямоугольные координаты вектора и точки . Рассмотрим произвольную точку и единичные взаимно-перпендикулярные

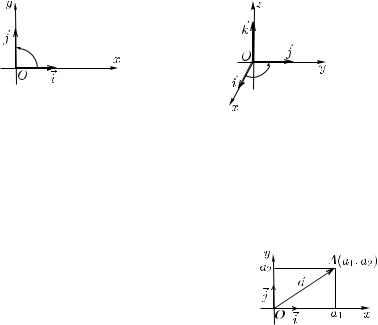
шается против часовой стрелки (рис. 3.7), а в случае пространства —

шающимся против часовой стрелки (рис. 3.8). Тогда говорят, что на плоскости (в пространстве) задана прямоугольная (или декартова) система координат ( ).

Пусть ( 1, 1, 1) и ( 2, 2, 2) — произвольные точки простран-

−−→

ства. Тогда = ( 2 − 1, 2 − 1, 2 − 1).

3.26. Представить вектор = (1, 2) в виде линейной комби-

нации векторов −

= (1, 1) и = ( 1, 1).

3.27. Представить вектор = (3, 1) в виде линейной комби-

нации векторов −

= (1, 1) и = ( 1, 1).

3.28. Представить вектор = (1, 1, 1) в виде линейной комбинации векторов 1 = (1, 1, −1), 2 = (1, −1, 1) и 3 = (−1, 1, 1).

3.29. Представить вектор = (1, 1, 1) в виде линейной комбинации векторов 1 = (1, 0, 1), 2 = 1, 1, 0) и 3 = (0, 1, 1).

2 . Расстояние между двумя точками. Длина вектора . Расстояние между двумя произвольными точками ( 1, 1, 1) и( 2, 2, 2) пространства вычисляется по формуле

√

= ( 2 − 1)2 + ( 2 − 1)2 + ( 2 − 1)2, (3.2)

а между двумя точками ( 1, 1) и ( 2, 2) плоскости — по формуле

√

= ( 2 − 1)2 + ( 2 − 1)2. (3.3)

Длина вектора = ( 1, 2, 3) в пространстве вычисляется по формуле

√

| | = 21 + 22 + 23, (3.4)

а вектора = ( 1, 2) в плоскости — по формуле

√

| | = 21 + 22. (3.5)

3.30.Даны точки (0, 0), (3, −4), (−3, 4), (−2, 2) и

(10, −3). Определить расстояние между точками:

1) и , 2) и , 3) и , 4) и , 5) и , 6) и .

3.31. Построить треугольник АВС и определить его периметр, если координаты вершин имеют следующие значения:

3.32.На оси абсцисс найти точку, удаленную от точки(1, 3) на 5 единиц.

3.33.На оси ординат найти точку, удаленную от точки(4, −1) на 5 единиц.

3.34.Найти точку, удаленную на 5 единиц как от точки(2, 1), так и от оси .

76Глава 3. Векторы на плоскости и в пространстве

3.35.На оси ординат найти точку, одинаково удаленную от начала координат и от точки (−2, 5).

3.36.На оси абсцисс найти точку, одинаково удаленную от начала координат и от точки (8, 4).

3 . Деление отрезка в данном отношении. Пусть и –

произвольные точки пространства. Говорят, что точка , лежащая на прямой , делит отрезок в отношении , если

−−→ −−→

= .

П р и м е р 3.3. По координатам точек ( 1, 1, 1) и ( 2, 2, 2) найти координаты точки ( , , ), которая делит отрезок в от-

то в координатной записи равенство (3.6) эквивалентно следующим трем равенствам:

− 1 = ( 2 − ), − 1 = ( 2 − ), − 1 = ( 2 − ).

Решая эти равенства относительно , , и соответственно, получим искомые координаты точки :

= ( 1, 2, 3) и = ( 1, 2, 3) в пространстве коллинеарны тогда и

только тогда, когда их соответствующие координаты пропорциональны, т. е.

В случае векторов = ( 1, 2) и = ( 1, 2) в плоскости условие коллинеарности принимает вид:

3.37. Точка является серединой отрезка , соединяющего начало координат с точкой (−5, 2). Найти координаты точки .

3.38. Найти длину медиан в треугольнике с вершинами

а) (11, 3), (15, 23) и (31, 15),

б) (0, −3), (2, 4) и (10, 5),

в) (1, 5), (4, 0) и (0, 10).

3.39. Построить точки и , найти точку ( , ), делящую отрезок в отношении : = 3 : 2. Координаты точек и следующие:

а) (−2, 1), (2, 1),

б) (−2, 1), (3, 6),

в) (−3, 2), (2, 4).

3.40. Отрезок, ограниченный точками (1, −3) и (4, 3),

разделен на три равные части. Определить координаты точек деления.

3.41.Точки (−2, 1), (2, 3) и (4, −1) — середины сторон треугольника. Найти координаты его вершин.

3.42.Найти сумму ординат середин сторон треугольникас вершинами в точках (3, 4), (7, 12) и (15, 8).

78Глава 3. Векторы на плоскости и в пространстве

3.43.Даны точки (1, 0), (5, 1) и (2, 3). Найти вектор

−−→ −−→ −−→

′ + ′ + ′, где ′, ′ и ′ — середины сторон , и

соответственно.

3.44. Точки (1, 0), (5, 1) и (2, 3) являются вершинами параллелограмма . Найти координаты вершины и точки пересечения диагоналей параллелограмма.

3.45. Точки (0, 0, 0), (2, 3, 0), (6, 3, 0) и ′(1, 1, 4) являются вершинами параллелепипеда ′ ′ ′ ′. Найти ко- ординаты вершин , ′, ′ и ′ и центра параллелепипеда.

3.46. Являются ли векторы и коллинеарными?

3.47.Доказать, что четырехугольник с вершинами (−1, 0),(2, 0), (3, 1) и (0, 1) является параллелограммом. Вычислить длину диагоналей этого параллелограмма.

3.48.Доказать, что четырехугольник с вершинами в точках(2, 1), (6, −3), (5, 6) и (3, 8) является трапецией и вычис-

лить длину оснований этой трапеции.

3.49. Отрезок с концами в точках (1, 5) и (8, −2) разделен на три равные части точками и . Найти координаты точек и .

(6, 0). Вычислить длину медиан этого треугольника.

3.52.Определить координаты вершин треугольника, если известны середины его сторон: (1, 1), (2, −2) и (4, 3).

3.53.Даны вершины треугольника: (3, −2, 1), (3, 1, 5) и

(4, 0, 3). Найти координаты точки пересечения медиан этого треугольника.

§3.4. Скалярное произведение двух векторов

Скалярным произведением двух ненулевых векторов и назы-

вается число, равное произведению длин этих векторов на косинус угла между ними:

где = \( , ) — угол между векторами и .

Скалярное произведение двух векторов имеет следующие основные свойства:

3) ( ) · = ( · ).

В прямоугольных координатах скалярное произведение векторов

= ( 1, 1, 1) и = ( 2, 2, 2) вычисляется по формуле

Косинус угла между двумя векторами = ( 1, 1, 1) и = = ( 2, 2, 2) вычисляется по формуле:

Два ненулевых вектора = ( 1, 1, 1) и = ( 2, 2, 2) взаимно

перпендикулярны тогда и только тогда, когда = 0, что равносильно равенству

1 2 + 1 2 + 1 2 = 0

(условие взаимной перпендикулярности векторов ).

3.54.Найти , если

в) (0, 0), (−1, 2), (6, −3).

3.58. Найти векторы единичной длины, перпендикулярные вектору :

3.59. Найти векторы единичной длины, перпендикулярные вектору и лежащие в плоскости = 0:

3.60. Найти векторы единичной длины, перпендикулярные вектору и лежащие в плоскости = 0:

3.61. Найти косинусы углов между вектором и координатными осями, если