
П.Геворкян. Сборник задач по высшей математике
.pdf§ 4.4. Модель международной торговли |
101 |
|
|
Дана структурная матрица торговли . Как должны соот-
носиться национальные доходы трех стран, чтобы торговля была сбалансированной?
|
4 |
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
1 |
|
3 |
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9 |
|
|
|
|
10 |
10 |
2 |
|
8 |
|
4 |
||||||||||||||||||
4.87. = |
3 |
|
|
|
|
2 |
|
|
|
|
2 |
. |
4.88. = |
4 |
|
8 |
|
2 |
. |
||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
3 |
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
2 |
1 |
|
1 |
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
5 |
|
|
|
|
5 |
|
|
4 |
|
4 |
|
4 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
3 |
|
|
2 |
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
10 |
|
|
|
8 |
7 |
|
8 |
|
4 |
||||||||||||||||||
4.89. = |
12 |
|
2 |
|
|
|
8 |
. |
4.90. = |
7 |
|
4 |
|
8 |
. |
||||||||||||||
|
5 |
|
1 |
|
|
|
1 |
|
|
4 |
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
2 |
|
|
|
1 |
1 |
|
5 |
|
5 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
5 |
|
|
|
2 |
|
|
7 |
|
8 |
|
8 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5 |
|
1 |
|
|
|
|
1 |
|
1 |
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7 |
|
|
9 |
|
8 |
|
|
5 |
|
6 |
|
10 |
|||||||||||||||||
4.91. = |
7 |
|
|
9 |
|
2 |
|
. |
4.92. = |
5 |
|
6 |
|
10 |
. |
||||||||||||||
|
3 |
|
|
2 |
|
1 |
|
|
|
|
1 |
|
1 |
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
2 |
|
3 |
|
|
3 |
|
2 |
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
9 |
|
8 |
|
|
|
|
5 |
|
3 |
|
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
2 |
|
3 |
|
|
|
|
1 |
|
1 |
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
9 |
|
|
9 |
|
5 |
|
|
6 |
|
9 |
|
5 |
|||||||||||||||||
4.93. = |
9 |
|
|
9 |
|
5 |
|
. |
4.94. = |
3 |
|
9 |
|
5 |
. |
||||||||||||||
|
1 |
|
|
4 |
|
1 |
|
|
|
|
1 |
|
5 |
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
5 |
|
|
|
|
2 |
|
3 |
|
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
4 |
|
|
3 |
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
9 |
|
|
9 |
|
7 |
|
|
13 |
|
|
7 |
5 |
|||||||||||||||||
4.95. = |
9 |
|
|
9 |
|
7 |
|
. |
4.96. = |
13 |
|
|
7 |
5 |
. |
||||||||||||||
|
4 |
|
|
4 |
|
5 |
|
|
|
|
4 |
|
|
2 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
|
|
4 |
|
1 |
|
|
5 |
|
|
2 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
9 |
|
7 |
|
|
|
|
13 |
|
|
7 |
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Г л а в а 5
Прямые линии на плоскости
§ 5.1. Уравнения прямой на плоскости
Прямая на плоскости в прямоугольной декартовой системе координат может быть задана уравнением одного из следующих
видов.
1 . Уравнение прямой с угловым коэффициентом :
|
= + , |
|
|
(5.1) |
|||
( = tg ) и называется угловым( |
|
|
) |
|
|
|
|
|
|
|
|
|
|||
̸= 2 |
|
|
|||||
где равен тангенсу угла |
|
|
наклона |
прямой к оси |
|||
|
|
коэффициентом, |
|
— величина от- |
|||
резка, отсекаемого прямой на оси .
2 . Уравнение прямой, проходящей через0( 0, 0) с данным угловым коэффициентом :
− 0 = ( − 0).
3 . Уравнение прямой, проходящей через точку раллельной направляющему вектору ( , ):
− 0 = − 0 .
данную точку
(5.2)
0( 0, 0) и па-
(5.3)
Уравнение (5.3) называется каноническим уравнением прямой . 4 . Уравнение прямой, проходящей через две данные точки
0( 0, 0) и 1( 1, 1):
− 0 |
= |
− 0 |
. |
(5.4) |
1 − 0 |
|
1 − 0 |
|
|
5 . Общее уравнение прямой на плоскости : |
|
|||
+ + = 0, |
(5.5) |
|||

§ 5.1. Уравнения прямой на плоскости |
103 |
|
|
где , , — произвольные коэффициенты ( и не равны нулю
одновременно).
Вектор = (− , ) является направляющим вектором прямой,
заданной общим уравнением (5.5).
Если ни один из коэффициентов уравнения (5.5) не равен нулю, то это уравнение можно преобразовать к виду
|
|
|
|
|
|
+ |
|
= 1, |
(5.6) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
где = − |
|
и = − |
|
— величины отрезков, которые отсекает пря- |
|||||
|
|
||||||||
|
|
||||||||
мая на координатных осях. Уравнение (5.6) называется |
уравнением |
||||||||
прямой «в отрезках».
П р и м е р 5.1. Составить уравнение прямой, отсекающей на осиотрезок = 3 и образующей с осью угол = 30 .
Р е ш е н и е. Находим угловой коэффициент: = tg = tg 30 =
1 = √ . Подставляя и в уравнение (5.1), получаем искомое уравне-
3
ние прямой:
1= √ + 3. 2
3
П р и м е р 5.2. Составить уравнение прямой, проходящей через(2, 1) и образующей с осью угол = 45 .
Р е ш е н и е. Находим угловой коэффициент: = tg 45 = 1. Подставляя данные координаты и значение в уравнение (5.2), получаем:
− 1 = 1 · ( − 2),
или
− − 1 = 0. 2
Пр и м е р 5.3. Составить уравнение прямой, проходящей через точки (3, 1) и (5, 4).
Р е ш е н и е. Подставляя данные координаты точек и в уравнение (5.4), получаем:
− 3 = − 1, 2 3
или
3 − 2 − 7 = 0. 2
П р и м е р 5.4. Прямая задана уравнением 3 − 5 − 45 = 0. Составить для этой прямой уравнение «в отрезках».

104Глава 5. Прямые линии на плоскости
Ре ш е н и е. Перенесем свободный член в правую часть и разделим полученное уравнение на 45. В результате получим:
15 + −9 = 1. 2
5.1. Составить уравнение прямой, проходящей через начало координат и составляющей с осью угол: а) 45 , б) 60 , в) 120 ,
г) 135 .
5.2.Построить прямую, отсекающую на оси отрезок
= 3 и составляющую с осью угол а) 45 , б) 135 . Напи-
сать уравнения этих прямых.
5.3.Построить прямую, отсекающую на оси отрезок
= −3 и составляющую с осью угол а) 60 , б) 120 . На-
писать уравнения этих прямых.
5.4. Определить параметры и (см. (5.1)) и построить прямые:
а) 2 − 3 = 6, |
б) 2 + 3 = 0, |
в) 3 + 4 = 12, |
г) 2 − 5 = 0, |
д) 2 + 5 = 0, |
е) = −3. |
5.5.Написать уравнение прямой, параллельной оси и отсекающей на оси отрезок, равный: а) 4, б) −5 и в) 0.
5.6.Написать уравнение прямой, проходящей через точку
и составляющей с осью угол :
а) (2, 3) , |
= 45 , |
б) (1, −2) , |
= 135 , |
в) (−2, 1) , |
= 45 . |
5.7. Написать уравнение пучка прямых, проходящих через точку (2, 3). Выбрать из этого пучка прямые, составляющие с осью углы а) 45 , б) 60 , в) 135 , г) 0 . Построить прямые.
5.8. Составить уравнение прямой, проходящей через начало координат и через точку с координатами (−2, 3), и построить ее.
§ 5.1. Уравнения прямой на плоскости |
105 |
|
|
5.9.Написать уравнение прямой, проходящей через точки
(−1, 3) и (4, −2).
5.10.Найти, какие три из точек (1, 3), (−2, 1), (−1, 7),(3, 1) лежат на одной прямой.
5.11.Написать уравнение прямой, проходящей через точки
и , и найти длину отрезка . Координаты точек взять
следующие:
а) (−2, 0), |
(2, 4), |
б) (14, −1), |
(6, 5), |
в) (12, 2), |
(6, −6). |
5.12.Дан треугольник с вершинами (4, 2), (−2, 4),
(−1, 1). Написать уравнение медианы .
5.13.В треугольнике с вершинами (−2, 0), (2, 6), (4, 2) написать уравнение стороны . Найти длину и написать уравнение медианы .
5.14.Дан треугольник с вершинами (2, 3), (6, 7),
(8, 1). Найти длину и написать уравнение средней линии, параллельной стороне .
5.15.Дан треугольник с вершинами (−2, 0), (2, 4),
(4, 0). Написать уравнение медианы .
5.16.Дан треугольник с вершинами (−2, 0), (2, 4),
(4, 0). Написать уравнение стороны и найти длину медианы .
5.17.Следующие уравнения прямых привести к виду «в от-
резках»:
а) 2 − 3 = 6,
б) 3 − 2 + 4 = 0,
в) 5 − 2 = 0,
г) −3 + = 1.
106Глава 5. Прямые линии на плоскости
§5.2. Нормальный вектор прямой. Расстояние
от точки до прямой
Вектор, перпендикулярный данной прямой, называется ее нормальным вектором.
= ( , ) является нормальным вектором прямой, заданной об-
щим уравнением |
|
|
+ + = 0. |
|
(5.7) |
1 . Уравнение прямой, проходящей через точку |
0 ( 0, 0) пер- |
|
пендикулярной вектору = ( , ), имеет вид: |
|
|
( − 0) + ( − 0) = 0. |
|
(5.8) |
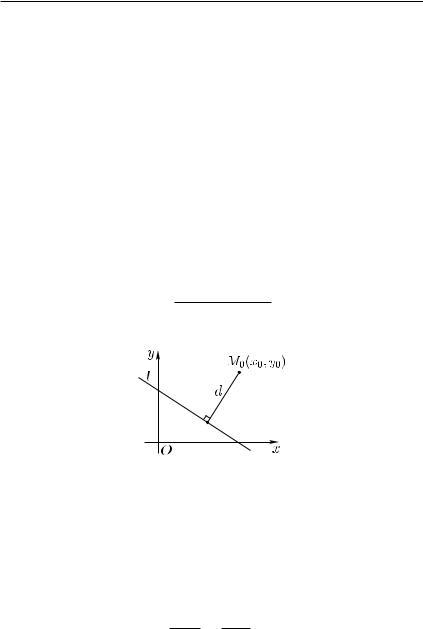
2 . Расстояние от точки 0( 0, 0) до прямой |
(рис. 5.1), |
|
заданной общим уравнением (5.7), вычисляется по формуле:
= |
| 0 + 0 + | |
. |
(5.9) |
||
|
|
|
|||
|
√ 2 + 2 |
|
|||
Рис. 5.1 |
|
П р и м е р 5.5. Дан треугольник с вершинами (2, 0), |
(2, 4), |
(4, 0). Написать уравнение высоты и найти длину этой высоты.
Ре ш е н и е. Составим уравнение прямой, проходящей через точкии (см. формулу (5.4)):
− 2 |
= |
− 4 |
, |
|
4 − 2 |
0 − 4 |
|||
|
|
или
2 + − 8 = 0.

§ 5.2. Нормальный вектор прямой. Расстояние от точки до прямой 107
= (−1, 2) является направляющим вектором этой прямой. Напишем уравнение прямой, проходящей через вершину (2, 0) и перпендикулярной стороне (см. формулу (5.8)):
−1 ( − 2) + 2 ( − 0) = 0,
или
− 2 − 2 = 0.
Теперь для определения расстояния от вершины (2, 0) до стороны воспользуемся формулой (5.9):
|
|2 · 2 + 1 · 0 − 8| |
|
|
|
|
4√ |
|
|
|||
= |
= |
4 |
|
= |
5 |
. 2 |
|||||
|
|
|
|
|
|
||||||
|
√22 + 12 |
√5 |
5 |
|
|
||||||
5.18. Найти длину высоты в треугольнике с вершинами:
а) (−6, 0), (2, 7) и (13, 2), б) (−2, 1), (3, 2) и (2, −3), в) (−3, 0), (2, 5) и (3, 2).
5.19.Найти расстояние от начала координат до прямой
+ − 2 = 0.
5.20.Найти расстояние от точки (2, 5) до прямой 6 +8 −
−5 = 0.
5.21.Найти расстояние между двумя параллельными прямыми 3 + 4 − 12 = 0 и 3 + 4 + 13 = 0.
5.22.Найти длину и уравнение высоты в треугольникес вершинами (−3, 0), (2, 5) и (3, 2).
5.23.По данным уравнениям сторон треугольника 2 − + +3 = 0, + 6 − 7 = 0, 3 + 2 − 9 = 0 составить уравнение
высоты, опущенной на первую сторону.
5.24. Написать уравнение прямой, удаленной от точки(4, −2) на четыре единицы и параллельной прямой 8 − 15 =
= 0.

108 |
Глава 5. Прямые линии на плоскости |
|
|
5.25. Написать уравнение прямой, если точка (2, 3) слу-
жит основанием перпендикуляра, опущенного из начала координат на эту прямую.
5.26.Найти уравнение прямой, проходящей через точку(−4, 3) и удаленной от начала координат на расстояние 5.
5.27.Через точку (1, 2) провести прямую, расстояния до которой от точек (2, 3) и (4, −5) были бы равны.
§ 5.3. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух
прямых
1 . Угол между двумя прямыми.
Пусть прямые 1 и 2 заданы уравнениями с угловым коэффициентом:
= 1 + 1 |
(5.10) |
и |
|
= 2 + 2. |
(5.11) |
Тогда угол (наименьший из углов, отсчитываемый против часовой стрелки) (рис. 5.2) между этими прямыми определяется по формуле:
tg = |
2 − 1 |
. |
(5.12) |
|
1 + 1 2 |
|
|
Рис. 5.2 |

§ 5.3. Угол между двумя прямыми |
|
|
109 |
||||
|
|
|
|
|
|
||
Если прямые 1 и 2 заданы общими уравнениями: |
|
||||||
1 + 1 + 1 = 0 |
|
|
(5.13) |
||||
и |
|
|
|
|
|
|
|
2 + 2 + 2 = 0, |
|
|
(5.14) |
||||
то угол между ними вычисляется по формуле: |
|
|
|
||||
cos = |
|
1 2 |
+ 1 2 |
|
. |
(5.15) |
|
|
|
|
|
|
|||
√ 12 + 12 · √ 22 + 22 |
|
||||||
|
|
|
|
||||
2 . Условия параллельности и перпендикулярности двух
прямых. Прямые, заданные уравнениями (5.10) и (5.11), параллельны тогда и только тогда, когда выполняется равенство
|
|
|
|
|
|
1 = 2, |
|
|
|
|
(5.16) |
||||
и перпендикулярны тогда и только тогда, когда |
|
|
|
||||||||||||
|
|
|
|
1 · 2 = −1. |
|
|
(5.17) |
||||||||
Прямые, заданные уравнениями (5.13) и (5.14), параллельны то- |
|||||||||||||||
гда и только тогда, когда выполняется равенство |
|
|
|
||||||||||||
|
|
|
|
|
1 |
= |
|
1 |
, |
|
|
|
|
(5.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
и перпендикулярны тогда и только тогда, когда |
|
|
|
||||||||||||
|
|
|
|
1 2 + 1 2 = 0. |
|
|
(5.19) |
||||||||
П р и м е р 5.6. Две прямые заданы уравнениями |
= |
2 + 3 и |
|||||||||||||
= −3 + 2. Найти угол между этими прямыми. |
|
|
|
||||||||||||
Р е ш е н и е. Имеем 1 = 2, 2 = −3. Поэтому по формуле (5.12) |
|||||||||||||||
находим |
|
−3 |
− 2 |
|
|
|
|
|
|||||||
|
|
|
|
tg = |
|
|
= 1. |
|
|
|
|||||
1 + (−3) · |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, угол между данными прямыми равен /4. |
2 |
||||||||||||||
П р и м е р 5.7. Показать, что прямые 4 −6 + 7 = 0 и 12 −18 − |
|||||||||||||||
−4 = 0 параллельны. |
|
|
|
|
|
|
|
|
|
|
|
||||
Р е ш е н и е. Проверим условие |
|
параллельности |
двух |
прямых |
|||||||||||
(см. (5.18)): |
4 |
= |
−6 |
. Следовательно, прямые параллельны. |
2 |
||||||||||
12 |
−18 |
||||||||||||||

110Глава 5. Прямые линии на плоскости
Пр и м е р 5.8. Показать, что прямые 3 −5 +7 = 0 и 10 +6 −3 = = 0 перпендикулярны.
Р е ш е н и е. Проверим условие перпендикулярности двух прямых (см. (5.19)): 3 · 10 + (−5) · 6 = 0. Следовательно, прямые перпендику-
лярны. 2
5.28. Определить угол между прямыми:
а) 5 − + 7 = 0 и 2 − 3 + 1 = 0, б) 2 + = 0 и = 3 − 4, в) 3 + 2 = 0 и 6 + 4 + 9 = 0.
5.29. Дан треугольник с вершинами (2, −1), (1, 1) и
−− ^
( 2, 3). Определить угол .
5.30. Дан треугольник с вершинами (−2, 1), (3, 2) и
− ^
(2, 3). Определить угол .
5.31. Построить треугольник, стороны которого заданы уравнениями: + = 4, 8 − = 0, − 3 − 8 = 0. Найти
углы треугольника.
5.32. Среди прямых указать параллельные и взаимно перпендикулярные:
а) 3 + 2 + 6 = 0, 3 + 2 = 0, 2 − 3 + 6 = 0, = −32 + 8, 5 + 15 + 3 = 0.
б) 3 −2 +7 = 0, 6 −4 −9 = 0, 6 +4 −5 = 0, 2 +3 −6 = 0.
5.33.Написать уравнение прямой, отсекающей от оси отрезок = −3 и перпендикулярной прямой 3 − 5 = 7.
5.34.Написать уравнение прямой, отсекающей от оси отрезок = 5 и параллельной прямой 2 + = 8.
5.35.Написать уравнение прямой, отсекающей от оси отрезок = 1 и перпендикулярной прямой 2 + 3 = 7.
