
П.Геворкян. Сборник задач по высшей математике
.pdf
§ 15.4. Интегрирование рациональных функций |
221 |
|
|
суммы простейших рациональных дробей :
( ) |
= |
|
11 |
|
|
+ |
|
|
|
12 |
|
|
|
+ · · · + |
|
|
1 1 |
|
|
+ . . . |
|
|
|
|
|||||||||||||||||||
( ) |
|
− |
|
1 |
|
|
( |
− |
)2 |
( |
|
) 1 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
· · · + |
|
|
1 |
|
|
+ |
|
|
|
|
2 |
|
|
|
|
+ · · · + |
|
|
|
|
|
|
+ |
|
|
|
||||||||||||||
|
|
|
|
|
− |
|
|
|
( |
)2 |
( |
|
) |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|||||||||
|
|
+ |
|
11 + 11 |
+ · · · + |
|
|
1 1 + 1 1 |
|
+ . . . |
|
|
|||||||||||||||||||||||||||||||
|
|
2 + 1 + 1 |
|
|
( 2 + 1 + 1) 1 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
||||||||||||||||||
|
· · · |
+ |
|
|
|
|
|
|
|
|
|
|
1 |
|
+ · · · + |
|
|
|
|
|
= |
|
|||||||||||||||||||||
|
|
2 + + |
( 2 + + ) |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
∑ |
∑ |
|
|
|
|
|
∑∑ |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (15.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
( + + ) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
=1 =1 |
|
|
|
|
|
|
|
|
=1 =1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
где , и — некоторые действительные числа.
Для отыскания неизвестных постоянных , и в разло- жении (15.4) используется метод неопределенных коэффициентов.
П р и м е р 15.9. Разложить рациональную дробь
3 2 − 7 + 2
( − 1)2
всумму простейших дробей.
Ре ш е н и е. Искомое разложение имеет вид
3 2 − 7 + 2 |
= |
|
+ |
|
|
+ |
|
|
|
, |
|
|
|
|
|
|
|
|
|||||
( − 1)2 |
|
|
− 1 |
( − |
1)2 |
||||||
|
|
|
|
|
|||||||
где , и — неизвестные постоянные.
Приводя правую часть к общему знаменателю и приравнивая чис-
лители, получаем тождество |
|
3 2 − 7 + 2 = ( − 1)2 + ( − 1) + . |
(15.5) |
Приравнивание коэффициентов при одинаковых степенях дает сис-
тему уравнений:
+ = 3,
−2 − + = −7,= 2,

222 Глава 15. Неопределенный интеграл
откуда получаем = 2, = 1, = −2. Итак, искомое разложение имеет вид:
3 2 − 7 + 2 |
= |
|
2 |
|
+ |
|
1 |
− |
2 |
. |
|
( − 1)2 |
|
− 1 |
( − 1)2 |
||||||||
|
|
|
|||||||||
В этом примере коэффициенты , , можно определить дру-
гим способом, полагая последовательно в тождестве (15.5) значения= 0, = 1 и, например, = 2. При = 0 находим = 2, при = 1
получаем = −2, а при = 2 имеем + 2 + 2 = 0, т. е. = 1. 2
В силу теоремы 15.4 интегрирование правильных рациональных дробей сводится к интегрированию простейших рациональных дробей
следующих четырех типов: |
|
|
|
|
|
|
|
|
|
|
||
|
(I) |
|
|
|
|
|
|
|
|
|||
|
|
; |
(II) |
|
|
; |
|
|
||||
|
− |
( − ) |
|
|
||||||||
(III) |
+ |
|
|
; (IV) |
|
|
|
+ |
|
, |
||
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
( |
2 |
+ + ) |
|
|||||
|
+ + |
|
|
|
|
|||||||
где > 1, > 1, а и — некоторые постоянные.
Проиллюстрируем метод интегрирования рациональных дробей на примерах.
П р и м е р 15.10. Найти |
Z 2 + 2 + 5. |
|
|
|
|
Р е ш е н и е. Подынтегральная функция является простейшей
дробью типа (III). Данный интеграл вычисляется выделением полного квадрата в неприводимом квадратном трехчлене 2 + + 1:
Z |
|
= Z |
( + 1) |
|
1 |
|
|
|
+ 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
= |
|
|
arctg |
|
+ . 2 |
||||||||
2 + 2 + 5 |
( + 1)2 + 4 |
2 |
2 |
||||||||||||||||||
|
П р и м е р 15.11. Найти Z 2 |
− 5 + 4. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Р е ш е н и е. Дробь |
|
|
|
правильная, ее разложение в сум- |
||||||||||||||||
|
2 − 5 + 4 |
|
|||||||||||||||||||
му простейших дробей имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
= |
|
+ |
|
. |
||||||||||||
|
|
2 − 5 + 4 |
( − 1)( − 4) |
− 1 |
− 4 |
||||||||||||||||
Приводя правую часть к общему знаменателю и приравнивая числители, получаем тождество
1 = ( − 4) + ( − 1),


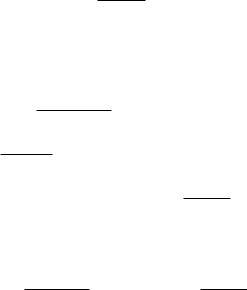
|
§ 15.5. Интегрирование квадратичных иррациональностей |
|
|
|
225 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
П р и м е р 15.12. Вычислить интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 − |
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Р е ш е н и е. |
|
Положим |
|
|
= |
|
3 sin . |
|
Тогда |
|
= |
|
3 cos , |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= arcsin |
|
|
. Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Z |
√ |
−2 |
|
|
|
|
|
|
Z √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
sin2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
9 sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
9 |
|
2 |
= |
|
|
9 |
− 9 sin2 |
|
3 cos = |
|
|
cos2 |
|
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
= |
|
1 − sin2 |
= |
|
|
|
|
|
|
|
= |
− |
ctg |
− |
+ = |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
sin2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Z |
sin2 |
|
|
|
|
Z |
|
− Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
9 − 2 |
|
arcsin |
|
+ . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Выше было применено преобразование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
sin2 |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√9 |
|
|
2 |
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
ctg = |
− |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Функция вида , √ |
|
|
, где , и — некоторые по- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 + + |
||||||||||||||||||||||||||||||||||||||||||||||||||
стоянные, называется(квадратичной |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иррациональностью |
|
|
|
|
|
||||||||||||||||||||
|
Вычисление интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z ( , √ |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ + |
|
|
|
|
|
|
|
|
|
(15.9) |
|||||||||||||||||||||||||||
сводится к одному из интегралов (15.6)– (15.8) посредством выделения
полного квадрата под радикалом и подходящего обозначения. |
|
||||||||||||||
|
П р и м е р 15.13. Найти Z |
|
( 2 + 4 + 13)3 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Р е ш е н и е. Выделяя |
|
√ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
полный квадрат в квадратном трехчлене, |
|||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Z |
|
|
|
Z |
|
|
|
|
Z |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
√ |
|
= |
√ |
|
= |
√ |
|
, |
|||||||
( 2 + 4 + 13)3 |
(( + 2)2 + 9)3 |
( 2 + 9)3 |
|||||||||||||
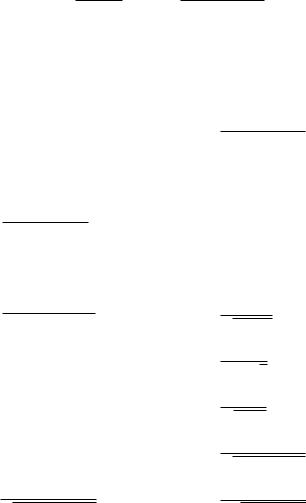
Г л а в а 16
Определенный интеграл
§ 16.1. Понятие определенного интеграла
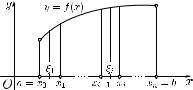
1 . Определенный интеграл как предел интегральной суммы. Пусть функция = ( ) определена на отрезке [ , ]. Разобьем отрезок [ , ] на произвольных частичных отрезков точками= 0 < 1 < 2 < · · · < = (рис. 16.1).
Рис. 16.1
Точки , = 0, 1, . . . , назовем точками разбиения отрезка [ , ]. Выберем в каждом из частичных отрезков [ −1, ], = 1, . . . , произвольную точку и составим сумму
|
|
|
|
|
= ( 1)Δ 1 + ( 2)Δ 2 + · · · + ( )Δ = |
∑ |
|
|
|
( )Δ , (16.1) |
||||
|
|
=1 |
|
|
где = − −1 — длина частичного отрезка |
[ −1, ], |
= |
||
= 1, . . . , . |
|
|
|
|
Сумма (16.1) |
называется интегральной суммой |
функции |
= |
|
= ( ) на отрезке |
[ , ]. |
|
|
|
Обозначим через длину максимального частичного отрезка дан-
ного разбиения, т. е. = max |
( = 1, . . . , ). |

228 Глава 16. Определенный интеграл
Если существует конечный предел
|
|
|
|
|
∑ |
|
|
lim |
( )Δ |
|
(16.2) |
→0 |
=1 |
|
|
независимо от способа разбиения отрезка |
[ , ] |
и выбора точек |
|
[ −1, ], = 1, . . . , , то он называется определенным интегралом
функции = ( ) на отрезке [ , ] и обозначается |
Z |
( ) . |
|
|
|
|
|
|
Итак, по определению
|
|
|
|
|
|
|
∑ |
( )Δ |
. |
|
|
Z ( ) = |
lim |
(16.3) |
|||
→0 =1 |
|
|
|
|
|
Если определенный интеграл (16.3) существует, то функция называется интегрируемой на отрезке [ , ]. Числа и называются соот-
ветственно нижним и верхним пределами интегрирования , ( ) — подынтегральной функцией , ( ) — подынтегральным выраже-
нием.
Фигура, ограниченная графиком функции ( ), осью и прямыми = и = ( < ), называется криволинейной трапецией .
Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции :
Z
= ( ) .
В этом и заключается геометрический смысл определенного интеграла.
Непрерывная на отрезке [ , ] функция ( ) интегрируема на этом отрезке.
2 . Основные свойства определенного интеграла .
1. Если функция ( ) определена в точке = , то |
Z |
( ) = 0. |
|
|
|
|
|
|
2. Если функция ( ) интегрируема на отрезке [ , ], то
|
|
|
Z |
( ) = − Z |
( ) . |
|
|
|
§ 16.1. Понятие определенного интеграла |
229 |
|
|
3. Если — постоянное число, а функция ( ) интегрируема на отрезке [ , ], то
Z |
Z |
|
|
( ) = ( ) .
|
|
|
|
4. Если функции ( ) и ( ) интегрируемы на отрезке |
[ , ], то |
||
справедливо равенство |
|
|
|
|
|
|
|
Z ( ( ) ± ( )) = |
Z ( ) ± Z ( ) . |
|
|
5. Если функция ( ) интегрируема на отрезке [ , ] и < < , то справедливо равенство
|
|
|
|
|
|
Z ( ) = |
Z ( ) + Z ( ) . |
(16.4) |
|
6. Если функция ( ) интегрируема на отрезке [ , ] и ( ) > 0 |
||||
для всех [ , ], |
то Z ( ) > 0. |
|
||
|
|
|
|
|
|
|
|
|
|
7. Пусть ( ) 6 ( ) для всех [ , ], тогда |
|
|||
|
|
|
|
|
|
Z ( ) 6 Z ( ) . |
|
||
8. Пусть ( ) |
интегрируема на отрезке [ , ]. Тогда | ( )| также |
|||
интегрируем на [ , ], причем |
|
Z |
|
|
|
Z |
|
||
|
|
|
|
|
( ) 6 | ( )| .
Т е о р е м а 16.1 (Лагранжа о среднем). Пусть ( ) непрерывна
на отрезке [ , ]. Тогда существует такая точка |
[ , ] что |
|
|
Z ( ) = ( )( − ). |
(16.5) |
