
П.Геворкян. Сборник задач по высшей математике
.pdf
§ 14.2. Направление выпуклости и точки перегиба графика функции 201
Т е о р е м а 14.4. Пусть функция ( ) дважды дифференцируема на интервале ( , ). Если ′′( ) < 0 ( ′′( ) > 0) для всех ( , ), то
график этой функции имеет выпуклость , направленную вверх (вниз) на интервале ( , ).
Рис. 14.2. Выпуклость, направленная вверх ( ); выпуклость, направленная вниз ( )
2 . Точки перегиба графика функции. Точка ( 0, ( 0))
( 0 ( , )) графика функции ( ) называется точкой перегиба этого графика, если существует окрестность точки 0, в пределах которой график функции ( ) слева и справа от 0 имеет разную направлен- ность выпуклостей (рис. 14.3).
|
y |
|
|
y =f(x) |
|
||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
a |
x0 |
b x |
|
|
|
|
|
|
||||
|
|
|
Рис. 14.3 |
|
|
|
|
Т е о р е м а 14.5 (необходимое |
условие |
точки перегиба). Пусть |
|||||
точка ( 0, ( 0)) есть точка перегиба графика функции |
= ( ). |
||||||
Тогда если функция = ( ) в точке 0 имеет непрерывную вторую производную, то она равна нулю: ′′( 0) = 0.
Т е о р е м а 14.6 (достаточное условие точки перегиба). Пусть функция ( ) дважды дифференцируема в некоторой окрестности
точки 0, причем ′′( 0) = 0. Если в пределах этой окрестности вторая производная ′′( ) имеет разные знаки слева и справа от

§ 14.3. Асимптоты графика функции |
203 |
|||
|
|
|
|
|
14.40. = ln(1 + |
3 |
). |
14.41. = |
. |
|
|
|||
14.42.= − 2 .
§14.3. Асимптоты графика функции
Прямая = называется вертикальной асимптотой графика функции = ( ), если
lim ( ) = ∞.
→
Непрерывные функции не имеют вертикальных асимптот. Прямая = + называется наклонной асимптотой графика
функции = ( ) при → +∞ ( → −∞), если эту функцию можно представить в виде
( ) = + + ( ),
где
→+∞ |
( →−∞ ( ) = 0). |
lim ( ) = 0 |
lim |
Т е о р е м а 14.7. Для того чтобы график функции ( ) имел наклонную асимптоту при → +∞, необходимо и достаточно , чтобы существовали конечные пределы
|
lim |
( ) |
= , |
|
lim [ ( ) |
− |
] = , |
(14.1) |
||||||
|
|
|
|
|||||||||||
→ |
+ |
∞ |
|
→ |
+ |
∞ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
причем тогда прямая = + будет наклонной асимптотой.
Эта теорема справедлива и в случае → −∞.
Пр и м е р 14.6. Найти асимптоты графика функции
= 2 + 3 + 5.
+ 1
Р е ш е н и е. Имеем:
lim1 |
2 + 3 + 5 |
= ∞, |
+ 1 |
||
→− |
|
|
и, следовательно, прямая = −1 — вертикальная асимптота.


§ 14.4. Общая схема исследования функций и построение графиков 205
2) исследовать функцию на четность-нечетность и периодич-
ность; 3) найти точки пересечения графика функции с осями координат;
4) найти асимптоты графика функции;
5) найти интервалы монотонности функции и точки экстремума; 6) найти интервалы выпуклости и точки перегиба графика функ-
ции.
2 + 3
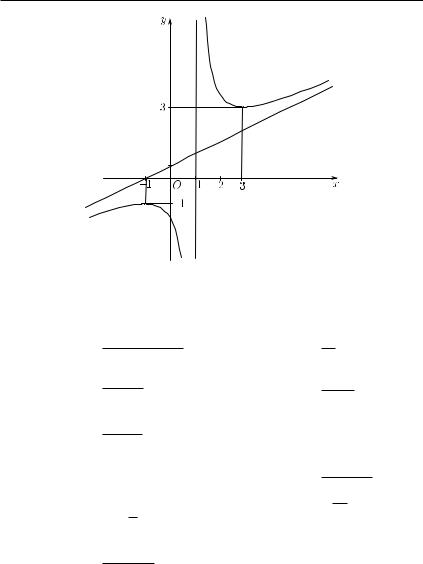
П р и м е р 14.7. Исследовать функцию = 2 − 2 и построить ее график.
1. Области определения функции не принадлежит только точка
= 1, то есть ( ) = (−∞, 1) (1, +∞).
2. Функция не является ни четной ни нечетной и не имеет пе-
риода.
3 3. Точка пересечения с осью : (0) = −2, т.е. имеем точку
(0, −2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как уравнение |
|
= 0 не имеет решения, следовательно, |
|||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||
график функции не имеет − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
точек пересечения с осью . |
|
|
|
|
|
||||||||||||||||||||
4. Так как |
lim |
2 + 3 |
|
|
= |
, то прямая = 1 — вертикальная |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
асимптота. |
→ |
|
|
− |
2 |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для нахождения наклонной асимптоты вычислим пределы: |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 + 3 |
|
1 + |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
= lim |
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
= |
|
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
→∞ (2 − 2) |
|
→∞ 2 |
− |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= →∞ ( |
2 + 3 1 |
|
) |
|
|
+ 3 |
|
|
|
|
1 + |
3 |
|
|
1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 − 2 − 2 · |
|
→∞ 2 − 2 |
|
|
|
|
→∞ 2 |
|
2 = |
2. |
|||||||||||||||||||||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
= |
lim |
|
|
|
|
|
= |
|
|
lim |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
является наклонной асимптотой графика |
|||||||||||||||||||||||||||
Значит, прямая = |
|
+ |
|
|
|||||||||||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||||||||||
функции как при → +∞, так и при → −∞. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
5. Для нахождения интервалов монотонности вычислим первую |
|||||||||||||||||||||||||||||||||||||
производную функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
′ = ′( ) = |
2 (2 − 2) − ( 2 + 3) · 2 |
|
= |
|
2 − 2 − 3 |
. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4( − 1)2 |
|
|
|
|
|
|
|
|
|
|
2( − 1)2 |
|
|
|||||||||


§ 14.5. Приложения производной в экономике |
209 |
|
|
П р и м е р 14.8. Цена реализуемой производителем продукции составляет 4000 руб. за единицу продукции. Известно, что издержки производителя определяются зависимостью ( ) = 1000 + 0, 1 3, где
— количество изготовленной и реализованной продукции. Каковы
оптимальный объем выпуска продукции и получаемый при этом доход?
Р е ш е н и е. Доход определяется разностью между выручкой за реализованную продукцию 4000 и себестоимостью этой продукции, т. е. ( ) = 4000 − (1000 + 0, 1 3) = 3000 − 0, 1 3.
При определении оптимального объема выпуска продукции следует найти производную функции ( ), приравнять ее к нулю и решить полученное уравнение: ′( ) = 3000 − 0, 3 2 = 0, 1 = 100 и2 = −100. Так как 2 < 0 и не имеет экономического смысла, то рассматриваем только 1 = 100. Нетрудно заметить, что 1 — точ- ка максимума. Следовательно, можно заключить, что оптимальный объем выпуска равен 100 единицам продукции.
Доход при оптимальном выпуске: (100) = 3000·100−0, 1·1003 =
=200 000 руб. 2
Пр и м е р 14.9. Зависимость объема выпущенной продукции от вложенного ресурса определена функцией ( ) = ln(27 + 4). Ука-
зать интервал изменения , на котором выполняется закон убывающей доходности.
Р е ш е н и е. Дифференцируем дважды данную функцию:
′( ) = (ln(27 + 4))′ |
|
3 |
||||||
= |
4 |
, |
|
|||||
27 + 4 |
||||||||
′′( ) = |
4 3 |
|
′ |
= |
324 2 − 4 6 |
. |
||
27 + 4 ) |
|
|
||||||
( |
|
|
(27 + 4)2 |
|||||
Решая уравнение ′′( ) = 0, находим = 3 (корни = 0 и = −3 не рассматриваем, так как > 0). Заметим, что = 3 — точка пере-
гиба, справа от этой точки функция является выпуклой вверх, следовательно, дополнительные затраты приводят к снижению объема выпуска продукции. Итак, закон убывающей доходности выполняется, когда (3, +∞). 2
14.68. Зависимость объема выпущенной продукции от
100
вложенного ресурса задана функцией ( ) = 1 + 100− . Ука-

210 Глава 14. Исследование функций
зать интервал изменения , на котором выполняется закон убывающей доходности.
10
14.69. Пусть ( ) = 100 + − 0, 1 — функция, выражающая зависимость объема произведенной продукции от вложен-
ного ресурса . Указать интервал изменения , на котором выполняется закон убывающей доходности.
14.70. Пусть ( ) = ln (500 + 3) — функция, выражающая зависимость объема произведенной продукции от вложенного ресурса . Указать интервал изменения , на котором выполня-
ется закон убывающей доходности.
14.71. Производитель реализует свою продукцию по цене 60 ден.ед. за единицу продукции. Издержки производителя определяются зависимостью ( ) = 30 +0, 001 3, где — коли-
чество изготовленной и реализованной продукции. Каковы оптимальный объем выпуска продукции и получаемый при этом доход?
14.72. Издержки производства единиц продукции определяются функцией ( ) = 0, 01 2 + 2 + 20. Цена одной единицы равна 10. Найти оптимальный объем выпуска и соответствующий ему доход.
14.73. Пусть даны функция дохода ( ) = 1000 − 2 и функция издержек ( ) = 5000 + 5248 − 196 2 + 3, зависящие от количества товара . Найти максимальную прибыль.
14.74. Пусть даны функция дохода ( ) = 1200 − 2 от продажи товара и функция издержек ( ) = 5000 + 8400 − −211 2 + 3 ( — количество товара). Найти максимальную прибыль.
14.75. Известна функция издержек ( ) = 1400 − 2 + +0, 0028 3, кроме того, известно, что весь товар реализуется по цене 100 ден.ед. за единицу. Найти максимальную прибыль, которую может получить фирма–производитель.
