
П.Геворкян. Сборник задач по высшей математике
.pdf
§ 7.1. Эллипс |
121 |
|
|
1) его полуоси, 2) координаты его фокусов, 3) эксцентриси-
тет.
7.2. Написать каноническое уравнение эллипса, зная, что а) расстояние между фокусами равно 8, а малая полуось
= 3, б) большая полуось = 6, = 0, 5.
7.3.Написать каноническое уравнение эллипса, проходящего через точки и с координатами:
а) (2, 3) и |
(1, 2 |
|
), |
б) |
(4, 5) |
и ( |
3 |
|
, 2), |
|||
|
|
3√5 |
|
|
|
9 |
|
|
5√5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
в) (2, 0) и (1, 2).
7.4. Эллипс, симметричный относительно осей координат, проходит через точки и . Написать его уравнение и найти
расстояние от точки до фокусов. Координаты точек следую-
щие: |
|
√ |
|
|
|
|
|
|
|
|
а) |
(2, |
|
|
|
|
|
(0, 2) |
, |
||
, |
|
|
||||||||
|
|
|
3) |
|
|
|
||||
б) (2√ |
|
, √ |
|
|
|
|||||
3 |
6), |
(6, 0). |
||||||||
7.5. На эллипсе 9 2 +25 2 = 225 найти точку , расстояние от которой до правого фокуса в четыре раза больше расстояния
до левого фокуса. |
|
√ |
|
|
|
|
7.6. Эллипс проходит через точку |
(−4, |
|
|
и имеет экс- |
||
21) |
||||||
|
|
|
||||
центриситет = 34. Написать уравнение эллипса и найти фокальные радиусы точки .
7.7.Определить траекторию точки , которая при своем движении остается вдвое ближе к точке (−1, 0), чем к прямой
= −4.
7.8.На прямой = −5 найти точку, одинаково удаленную от левого фокуса и от верхней вершины эллипса 2 + 5 2 = 20.
7.9.Написать уравнение окружности с центром (3,4) и радиусом =5. Лежат ли на этой окружности точки: (−1, 1),
(2, 3), (0, 0), (4, 1)?

122 |
Глава 7. Кривые второго порядка |
|
|
7.10. Написать уравнение окружности с центром (2, 1) и радиусом = 3 и построить ее. Лежат ли на этой окружности точки: (−1, 2), (2, 4), (0, 0)? Найти точки пересечения окружности с осями координат.
7.11.Определить траекторию точки , которая при своем движении остается вдвое ближе к точке (−1, 1), чем к точке
(−4, 4).
7.12.Дана точка (−4, 6). Написать уравнение окружности, диаметром которой служит отрезок .
7.13.Даны точки (4, 0) и (1, 4). Написать уравнение окружности, диаметром которой служит отрезок .
7.14.Построить окружности:
a) 2 + 2 − 4 + 6 − 3 = 0, |
б) 2 + 2 − 8 = 0, |
в) 2 + 2 + 4 = 0. |
|
7.15. Составить уравнение прямой, проходящей через центры окружностей 2 + 2 = 5 и 2 + 2 + 2 + 4 = 31. Найти
отношение радиусов этих окружностей.
§ 7.2. Гипербола
Геометрическое место всех точек плоскости, координаты которых в некоторой прямоугольной системе координат удовлетворяют
уравнению
2 |
− |
2 |
|
|
|
|
= 1, |
(7.4) |
|
2 |
2 |
|||
где > 0, > 0, называется гиперболой.
Система координат , в которой уравнение гиперболы имеет
вид (7.4), называется канонической (для этой гиперболы), а само уравнение (7.4) — каноническим уравнением гиперболы.
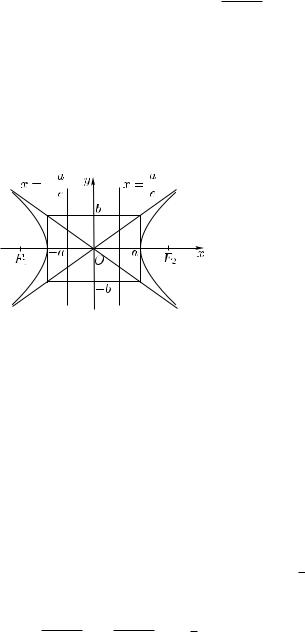
Гипербола имеет вид, изображенный на рис. 7.2.
Прямые = ± являются асимптотами гиперболы. Число называется действительной полуосью , а число — мнимой полуосью
гиперболы. Точки (± , 0) называются вершинами гиперболы. Точка
§ 7.2. Гипербола |
123 |
|
|
√
(0, 0) называется центром гиперболы. Число = 2 + 2 называ-
ется линейным эксцентриситетом |
гиперболы. Точки 1 = (− , 0) |
|||||||
и 2 = ( , 0) называются фокусами |
гиперболы. Число 2 называет- |
|||||||
|
|
|
|
|
|
|
|
|
ся фокусным расстоянием гиперболы. Число = |
|
называется экс- |
||||||
|
||||||||
|
|
|
|
|
2 |
|||
центриситетом гиперболы. Число = |
|
|
называется фокальным |
|||||
|
|
|||||||
параметром гиперболы. Прямые = ± |
|
называются директрисами |
||||||
|
|
|||||||
гиперболы (см. рис. 7.2).
Рис. 7.2
Гипербола (7.4) является геометрическим местом точек, абсолютная величина разности расстояний которых до фокусов равна 2 .
Это свойство гиперболы называется ее фокальным свойством.
П р и м е р 7.3. Построить гиперболу 2−4 2 = 16 и ее асимптоты. Найти фокусы и эксцентриситет гиперболы.
Р е ш е н и е. Приведем уравнение к каноническому виду (5.18), разделив его на 16:
2 |
− |
2 |
= 1. |
42 |
22 |
Итак, для нашей гиперболы = 4, = 2. Значит, прямые = ±12 являются ее асимптотами.
Найдем линейный эксцентриситет гиперболы:
√ √ √
= 2 + 2 = 42 + 22 = 2 5.
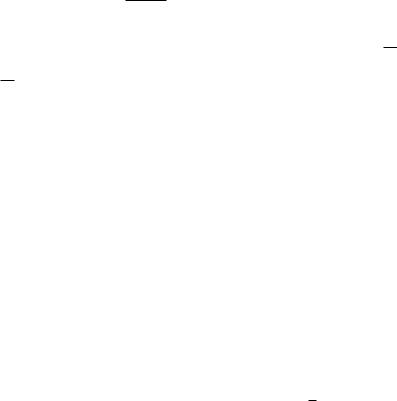
124 |
Глава 7. Кривые второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(−2√ |
|
, 0), 2 |
(2√ |
|
, 0). |
||||||||||||||
Значит, фокусами данной гиперболы будут: 1 |
5 |
5 |
||||||||||||||||||||
|
|
|
|
|
√ |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|||
|
Эксцентриситет гиперболы равен = |
|
= |
|
2 5 |
= |
5 |
. |
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
7.16. На гиперболе 2 −4 2 = 16 взята точка с ординатой, |
|||||||||||||||||||||
равной 1. Найти расстояние от точки до фокусов. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
2 |
||||||||
|
7.17. Найти расстояние от фокуса гиперболы |
|
|
|
|
= 1 |
||||||||||||||||
|
|
2 |
2 |
|||||||||||||||||||
до ее асимптот. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7.18. Найти координаты центра, вершин и уравнения асим-
4 − 5
птот гиперболы = − 1 .
2
7.19. Написать уравнения касательных к гиперболе 16−
− 2 = 1, проведенных из точки (0, −2).
4
7.20.Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы — в вершинах эллипса 9 2 + 25 2 = 225.
7.21.Составить уравнение гиперболы, если расстояние между ее вершинами равно 20, а расстояние между ее фокусами
равно 30.
7.22. Найти уравнение гиперболы, если ее действительная полуось равна 5, а эксцентриситет = 1, 4.
|
|
|
|
(3, |
|
√ |
|
|
|
) |
|
|
7.23. |
Гипербола проходит через точки |
2 |
15 |
и |
||||||||
|
5 |
|
||||||||||
√ |
|
|
. Найти уравнение гиперболы. |
|
|
|
|
|
|
|
|
|
(−2 5, 3) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
2 |
|
||||||
7.24. Найти уравнения асимптот гиперболы |
|
− |
|
= 1. |
|
|||||||
3 |
2 |
|
||||||||||
7.25. Уравнения асимптот гиперболы = ±2 , а расстояние между фокусами 2 = 10. Найти уравнение гиперболы.
§ 7.3. Парабола |
125 |
|
|
§ 7.3. Парабола
Геометрическое место всех точек плоскости, координаты которых в некоторой прямоугольной системе координат удовлетворяют
уравнению |
= 2 , |
|
2 |
(7.5) |
где > 0, называется параболой.
Система координат , в которой уравнение параболы имеет
вид (7.5), называется канонической (для этой параболы), а само уравнение (7.5) — каноническим уравнением параболы.
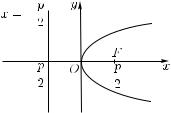
Ось абсцисс является осью симметрии параболы (7.5). Вид параболы (7.5) приведен на рис. 7.3.
Точка (0, 0) называется вершиной параболы. Ось называется осью параболы. Число называется фокальным параметром парабо-
лы. Точка = |
|
, 0 |
|
фокусом |
|
Число |
|
|
|||
|
|
|
|
|
|||||||
( |
2 |
) |
называется |
|
параболы. |
|
|
|
2 |
назы- |
|
вается фокусным расстоянием параболы. Прямая = − |
|
|
называется |
||||||||
2 |
|
||||||||||
директрисой параболы (см. рис. 7.3).
Рис. 7.3
Точка ( , ) принадлежит параболе (7.5) тогда и только то-
гда, когда она равноудалена от фокуса и директрисы.
Это свойство параболы называется ее директориальным свойством.
7.26.Построить параболу 2 = 6 , найти координаты ее фокуса и написать уравнение директрисы.
7.27.Написать уравнение параболы:
а) проходящей через начало координат и точку (1, −3),

126 |
Глава 7. Кривые второго порядка |
|
|
б) проходящей через начало координат и точку (2, −4) и симметричной относительно оси .
7.28.На параболе 2 = 6 найти точку, расстояние от которой до фокуса равно 92.
7.29.Какой кривой 2-го порядка соответствует уравнение:
a) 2 − 4 + 2 = 0,
б) 2 + 2 − 2 = 0,
в) 2 − 2 − + 1 = 0.
7.30. Найти расстояние от начала координат до прямой,
4 − 4
проходящей через центр гиперболы = 2 + 1 и вершину пара- болы = − 2 + 2 − 13.
7.31. Найти уравнения параболы и ее директрисы, если известно, что парабола симметрична относительно оси , а точка
пересечения прямых = и + = 2 лежит на параболе.
7.32. Найти расстояние от начала координат до прямой,
+ 1
проходящей через центр гиперболы = − 1 и вершину па- раболы = −2 2 + 5 − 2.

Г л а в а 8
Предел последовательности
§ 8.1. Понятие множества. Операции над множествами
Множество — это совокупность (собрание, семейство, класс и т. д.) каких-либо объектов произвольной природы. Объекты, из которых состоит данное множество, называются элементами этого множества.
означает, что элемент принадлежит множеству . Запись / или означает, что элемент не принадлежит множеству . Множество, не содержащее ни одного элемента, называется
пустым множеством и обозначается ?.
Множество называется подмножеством множества , если любой элемент множества также принадлежит множеству . Если является подмножеством , то пишут .
= — множества и совпадают (состоят из одних и тех же элементов).
— объединение множеств и .
∩ — пересечение множеств и .
— разность множеств и .
— дополнение множества .
N = {1, 2, 3, . . . } — множество натуральных чисел. Z = { 0, ±1, ±2, . . .} — множество всех целых чисел.
R — множество всех действительных чисел.
{ : ( )} — совокупность элементов множества , для которых выполнено ( ).

128Глава 8. Предел последовательности
Пр и м е р 8.1. Даны множества = { 1, 3, 6, 8} и = { 2, 4, 6, 8}. Найти , ∩ , .
Ре ш е н и е. Очевидно, что = { 1, 2, 3, 4, 6, 8}, ∩ = { 6, 8}
и= { 1, 3}. 2
8.1.= { N : = 2 , = 1, 2, 3, . . .}. Выяснить, являются ли числа 4, 6, 8, 10, 14, 16 элементами (записать ответ с использованием символов , /).
8.2.Верно ли равенство:
а) { : sin = 0} = Z, |
|
|
|
|
|
|
|
|
|
|
||||||||||
б) { : sin |
|
|
= 0} = Z? |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8.3. Как соотносятся множества: |
{ |
|
|
|
|
|
|
|||||||||||||
а) = |
|
: 3 |
|
|
= 0 и = |
|
|
: 2 |
|
= 0 |
||||||||||
б) = |
{ |
: 2 |
− |
= 0} и = |
|
|
: |
|
−1 = 0 ?}, |
|||||||||||
8.4. |
|
{ |
|
|
|
|
|
} |
|
|
|
|
|
|
− |
} |
||||
|
|
|
|
|
|
|
− |
|
∩ |
|
|
{ |
|
|
||||||
|
Построить |
|
|
|
|
, |
и |
|
, если: |
|
|
|
||||||||
а) = { 1, 3, 4} и = { 2, 3, 4, 5},
б) = { 2, 4, 7} и = { 2, 7, 10, 12},
в) = { 2, 4, 5} и = { 4, 5, 8, 10}.
8.5.Пусть — множество корней уравнения 2 −8 +15 = 0
и= { 2, 5}. Найти и ∩ .
8.6.Доказать, что, если есть множество корней уравнения
2 − 7 + 6 = 0 и = { 1, 6} , то = .
8.7.Пусть — множество корней уравнения 2 −3 +2 = 0. Проверить справедливость равенства = , если:
а) = { 1, 2}, б) = { 2, 3}, в) = { 1, 2, 3}.
8.8.Пусть — множество четных чисел, — множество простых чисел. Найти ∩ .
8.9.Пусть — множество чисел, кратных 2, — множество чисел, кратных 5. Найти ∩ .

§ 8.1. Понятие множества. Операции над множествами |
129 |
|
|
8.10.Пусть — множество чисел, оканчивающихся на 0,
— множество чисел, оканчивающихся на 5. Найти .
8.11.Пусть — множество чисел, кратных 3, — множество чисел, кратных 5. Найти ∩ .
8.12.Пусть — множество чисел, кратных 2, — множество чисел, кратных 3, — множество чисел, кратных 5. Найти
∩ ∩ .
8.13.Из 100 студентов английский язык изучают студентов, немецкий — студентов, французский— студентов, английский и немецкий — студентов, английский и французский — студентов, немецкий и французский — студентов, английский, немецкий и французский — студентов. Найти,
сколько студентов не изучают ни одного языка, сколько студентов изучают только один английский (немецкий, французский) язык, если:
а) = 42, = 30, = 28, = 10, = 8, = 5, = 3, б) = 41, = 29, = 32, = 14, = 10, = 8, = 5, в) = 37, = 31, = 29, = 15, = 10, = 7, = 5?
8.14. Определить, в каких из пар множеств одно множество является подмножеством другого:
а) и ∩ ,
б) и ,
в) ∩ и ∩ ,
г) ∩ и .
8.15. Какие из следующих множеств совпадают:
а) , б) ∩ , в) ∩ , г) ?
130 |
Глава 8. Предел последовательности |
|
|
§ 8.2. Предел последовательности
1 . Понятие последовательности. Если каждому натуральному числу = 1, 2, 3, . . . по некоторому закону поставлено в соответ-
ствие определенное действительное число , то говорят, что задана
числовая последовательность или просто последовательность
1, 2, 3, . . . , , . . . (8.1)
Числа 1, 2, . . . называются элементами или членами последовательности, а число — общим членом или -м членом последова-
тельности (8.1). Последовательность (8.1) кратко обозначается через { }. Чаще всего последовательность задается формулой его общего
члена.
2 . Понятие предела последовательности . Число назы- вается пределом последовательности { }, если для любого (сколь угодно малого) положительного числа существует такое натуральное число , зависящее от , что для всех натуральных чисел > выполняется неравенство
| − | < . |
(8.2) |
При этом пишут |
|
lim = |
(8.3) |
→∞ |
|
или
→
и говорят, что последовательность стремится (или сходится ) к .
Если последовательность { } имеет предел, то такая последо-
вательность называется сходящейся. В противном случае последовательность называется расходящейся.
3 . Геометрический смысл предела последовательности .
Справедливо следующее геометрическое определение предела последовательности.
Число называется пределом последовательности { }, если для любой -окрестности точки (т. е. интервала ( − , + )) существует
такое натуральное число , что все члены , для которых > , лежат в этой -окрестности точки (рис. 8.1). Другими словами: вне-окрестности точки лежит конечное число членов последовательности.
