
П.Геворкян. Сборник задач по высшей математике
.pdf§ 2.4. Однородные системы линейных уравнений |
61 |
|
|
Найти решения системы.
2 1 + 2 − 3 = 0,
2.61.1 + 2 2 + 3 = 0,2 1 − 2 + 3 3 = 0.
1 − 2 − 3 = 0,
2.62.1 + 4 2 + 2 3 = 0,3 1 + 7 2 + 3 3 = 0.
−5 1 + 2 + 3 = 0,
2.63.1 − 6 2 + 3 = 0,
1 + 2 − 7 3 = 0.
1 + 2 + 3 = 0,
2.64.3 1 + 6 2 + 5 3 = 0,1 + 4 2 + 3 3 = 0.
{
1 − 2 2 + 3 = 0,
2.65.3 1 − 5 2 + 2 3 = 0.
{
3 1 + 4 2 + 5 3 = 0,
2.66.1 + 2 2 − 3 3 = 0.
1 + 3 2 + 2 3 = 0,
2 1 − 2 + 3 3 = 0,
2.67.3 1 − 5 2 + 4 3 = 0,
1 + 17 2 + 4 3 = 0.
1 + 2 2 + 3 + 4 = 0,
2.68.2 1 + 5 2 + 3 + 5 4 = 0,3 1 + 8 2 + 2 + 9 4 = 0.
−2 1 + 2 + 3 = 0,
2.69.1 − 2 2 + 3 = 0,
1 + 2 − 2 3 = 0.
2 1 + 2 + 3 = 0,
2.70.1 + 2 2 + 3 = 0,1 + 2 + 2 3 = 0.
62 |
Глава 2. Системы линейных уравнений |
|
|
2 1 + 3 2 − 3 + 5 4 = 0,
3 1 − 2 + 2 3 − 7 4 = 0,
2.71.4 1 + 2 − 3 3 + 6 4 = 0,
1 − 2 2 + 4 3 − 7 4 = 0.
1 − 2 2 + 3 + 4 − 5 = 0,
2 1 + 2 − 3 − 4 + 5 = 0,
2.72.1 + 7 2 − 5 3 − 5 4 + 5 5 = 0,
3 1 − 2 − 2 3 + 4 − 5 = 0.
2.73.Определить, при каком значении система уравнений имеет только нулевое решение.
1 |
− 14 2 |
+ 15 3 |
= 0, |
3 1 |
2 2 |
+ 3 |
= 0, |
|
− |
|
|
1 + 2 2 − 3 3 = 0.
2.74.При каких система имеет ненулевые решения?
{
− 1 + 2 = 0,1 − 2 = 0.
Найти фундаментальную систему решений и общее решение данных систем линейных уравнений.
2.75. |
3 1 |
+ |
2 2 |
+ 3 |
+ 3 4 |
= 0, |
|||||
|
|
1 |
+ 2 |
+ 2 3 |
+ 4 |
= 0, |
|||||
|
|
|
3 |
|
3 |
|
|
|
|
||
|
|
2 1 + |
|
2 |
+ |
|
3 |
+ 2 4 = 0. |
|||
|
2 |
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
||
|
|
1 − |
2 + 3 − |
4 = 0, |
|||||||
2.76. |
|
1 |
+ |
2 |
+ 2 3 + |
3 4 = 0, |
|||||
|
|
2 1 + 4 2 + 5 3 + 10 4 = 0. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
{
3 1 + 4 2 + 3 + 2 4 = 0,
2.77. 1 − 2 + 3 − 4 = 0.
1 + 2 − 3 − 4 = 0,
2.78.1 + 2 2 − 3 + 3 4 = 0,
1 − 2 − 3 − 9 4 = 0.

§ 2.5. Модель многоотраслевой экономики Леонтьева |
63 |
|
|
{
2.79. |
|
1 + 2 2 + 3 + 4 + 5 = 0, |
|||||||||||
|
1 − 2 2 + 3 + 4 − 5 = 0. |
||||||||||||
|
|
|
1 − 2 2 + 3 = 0, |
||||||||||
2.80. |
|
|
|
2 1 − 2 |
− 3 = 0, |
||||||||
|
|
|
|||||||||||
|
|
|
|
2 1 + 4 2 − 2 3 = 0. |
|||||||||
|
− 1 + 2 2 + 3 3 + 4 4 = 0, |
||||||||||||
|
|
1 |
+ 2 |
3 |
+ 2 4 = 0, |
||||||||
|
|
|
|
1 |
+ 3 |
||||||||
|
|
2 |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
2.81. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
4 |
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
2 |
+ 3 |
+ |
|
4 = 0, |
||
|
|
|
|
|
|||||||||
|
|
3 |
3 |
|
|
|
|
3 |
|
||||
|
|
1 |
1 |
|
3 |
+ 4 = 0. |
|||||||
|
|
|
|
1 |
+ 2 |
+ 3 |
|||||||
|
|
4 |
2 |
|
4 |
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 2.5. Модель многоотраслевой экономики Леонтьева
Математическая модель межотраслевого баланса в статистической форме впервые была сформулирована в 1936 г. американским экономистом В.В. Леонтьевым.
Рассматривается экономическая система, состоящая из взаимо-
связанных отраслей производства. Продукция каждой отрасли частично идет на внешнее потребление ( конечный продукт ), а частично используется в качестве сырья в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением.
Обозначим через валовой выпуск продукции -й отрасли за планируемый период, а через — конечный продукт -й отрасли ( = 1, 2, . . . , ).
Пусть — часть продукции -й отрасли, которая потребляется-й отраслью для обеспечения выпуска ее продукции в размере
( , = 1, 2, . . . , ).
Тогда имеем систему балансовых соотношений:
2 |
− ( 21 |
+ 22 |
+ . . . |
+ 2 ) = 1 |
, |
(2.15) |
|
|
1 |
− ( 11 |
+ 12 |
+ . . . |
+ 1 ) = 1 |
, |
|
.................................................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ( 1 + 2 + . . |
. + ) = . |
|
||||
|
|
|
|
|
|
|
|
64 |
Глава 2. Системы линейных уравнений |
|
|||||
|
|
|
|
||||
Вектор-столбец = 2 |
называется ассортиментным век- |
||||||
|
|
|
1 |
|
|
||
|
|
· · · |
|
||||
|
|
|
|
|
|
|
|
тором, а = 2 |
|
|
|
|
|
||
— вектор-планом. |
|
||||||
|
1 |
|
|
|
|
|
|
· · · |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величины |
|
|
|
|
|
|
|
|
|
= |
|
|
( , = 1, 2, . . . , ) |
(2.16) |
|
|
|
|
|||||
|
|
|
|
|
|||
называются коэффициентами прямых затрат , они определяют затраты -й отрасли, используемые -й отраслью для производства ее
единицы продукции.
Если ввести матрицу прямых затрат (технологическую или
структурную) = ‖ ‖, то балансовые соотношения можно переписать в компактной матричной форме:
( − ) = , |
(2.17) |
где — единичная матрица.
Основная задача межотраслевого баланса: найти вектор валового выпуска , который при известной матрице прямых затрат
обеспечивает заданный вектор конечного продукта .
Неотрицательная квадратная матрица -го порядка > 0 (все> 0) называется продуктивной, если для любого вектора > 0 существует решение > 0 уравнения (2.17).
На практике часто используется следующее условие продуктивности матрицы. Неотрицательная квадратная матрица продук-
тивна, если максимум сумм элементов ее столбцов не превосходит единицу, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
Если — продуктивная матрица, то решение балансового уравнения (2.17) можно записать в виде
= ( − )−1 = , |
(2.18) |
где = ( − )−1 называется матрицей полных затрат .
§ 2.5. Модель многоотраслевой экономики Леонтьева |
65 |
|
|
П р и м е р 2.7. В следующей таблице представлен балансовый отчет для двухотраслевой модели экономики:
Отрасль |
Потребление продукции |
Валовой выпуск |
|
|
Энергетика |
Машиностр. |
|
Энергетика |
100 |
160 |
500 |
|
|
|
|
Машиностроение |
275 |
40 |
400 |
Вычислить необходимый объем валового выпуска каждой отрасли, обеспечивающий вектор выпуска конечной продукции
( )
200
= .
100
Р е ш е н и е. По формуле (2.16) находим матрицу коэффициентов прямых затрат:
= ( |
0,055, |
0, 1 ). |
|
2 |
0, 4 |
Очевидно, что эта матрица продуктивна.
Найдем матрицу полных затрат = ( − )−1: |
1, 6 ). |
||||||||||||
= ( − )−1 = 0, 5 |
( |
0,055, |
0, 8 |
) = |
( |
1, 1 |
|||||||
|
|
1 |
|
|
|
9 0, 4 |
|
|
1, 8 |
0, 8 |
|||
Итак, для вектора конечной продукции можно найти необхо- |
|||||||||||||
димый объем валового выпуска по формуле (2.18): |
|
||||||||||||
= ( |
1, 1 |
1, 6 |
|
) · ( |
100 |
) |
= ( |
380 |
). |
2 |
|||
|
1, 8 |
0, 8 |
|
|
|
200 |
|
|
440 |
|
|
||
В следующих таблицах приведен балансовый отчет для многоотраслевых экономических систем. Вычислить необходимый объем валового выпуска каждой отрасли, обеспечивающий вектор выпуска конечной продукции .
2.82.
Отрасль |
|
Потребление продукции |
Валовой |
|||
|
I |
|
|
II |
выпуск |
|
I |
180 |
|
|
60 |
1200 |
|
|
|
|
|
|
|
|
II |
240 |
|
|
180 |
600 |
|
|
|
|
|
|
|
|
|
|
= ( |
240 |
). |
|
|
|
|
|
420 |
|
|
|
66 |
Глава 2. Системы линейных уравнений |
|
|
2.83.
Отрасль |
Потребление продукции |
Валовой |
|||
|
|
|
|
|
|
|
I |
|
II |
выпуск |
|
|
|
|
|
|
|
I |
80 |
|
106 |
800 |
|
|
|
|
|
|
|
II |
240 |
|
106 |
530 |
|
|
= ( |
320 |
). |
|
|
2.84. |
110 |
|
|||
|
|
|
|
|
|
|
|
|
|||
Отрасль |
Потребление продукции |
Валовой |
|||
|
|
|
|
|
|
|
I |
|
II |
выпуск |
|
|
|
|
|
|
|
I |
143,75 |
|
231,25 |
575 |
|
II |
25,30 |
|
37 |
370 |
|
|
|
|
|
|
|
|
= ( |
250 |
). |
|
|
2.85. |
92 |
|
|||
|
|
|
|
|
|
|
|
|
|||
Отрасль |
Потребление продукции |
Валовой |
|||
|
I |
|
II |
выпуск |
|
I |
12 |
|
18 |
120 |
|
|
|
|
|
|
|
II |
12 |
|
6 |
|
60 |
|
|
|
|
|
|
|
( |
360 |
) |
|
|
|
= |
180 |
. |
|
|
|
|
|
|
||
2.86. |
|
|
|
|
|
|
|
|
|||
Отрасль |
Потребление продукции |
Валовой |
|||
|
|
|
|
|
|
|
I |
|
II |
выпуск |
|
|
|
|
|
|
|
I |
88,6 |
|
34,4 |
443 |
|
|
|
|
|
|
|
II |
12 |
|
6 |
|
191 |
|
|
|
|
|
|
|
= ( |
99 |
). |
|
|
|
|
390 |
|
|
|
§ 2.5. Модель многоотраслевой экономики Леонтьева |
67 |
|||||||
|
|
|
|
|
|
|
|
|
2.87. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отрасль |
|
Потребление продукции |
|
Валовой |
||||
|
I |
|
II |
|
|
III |
|
выпуск |
|
|
|
|
|
|
|
|
|
I |
79 |
|
106 |
|
|
300 |
|
790 |
|
|
|
|
|
|
|
|
|
II |
237 |
|
212 |
|
|
75 |
|
530 |
|
|
|
|
|
|
|
|
|
III |
158 |
|
53 |
|
|
150 |
|
750 |
|
|
= |
100 |
. |
|
|||
|
|
|
|
300 |
|
|
||
|
|
|
400 |
|
||||
2.88. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отрасль |
|
Потребление продукции |
|
Валовой |
||||
|
|
|
|
|
|
|
|
|
|
I |
|
II |
|
|
III |
|
выпуск |
|
|
|
|
|
|
|
|
|
I |
16 |
|
42 |
|
|
42 |
|
200 |
|
|
|
|
|
|
|
|
|
II |
12 |
|
21 |
|
|
21 |
|
300 |
|
|
|
|
|
|
|
|
|
III |
46 |
|
27 |
|
|
27 |
|
500 |
|
|
= |
164 |
. |
|
|||
|
|
394 |
|
|||||
|
|
|
|
794 |
|
|
||
2.89.Для задачи 2.83 найти необходимый объем валового выпуска отрасли, если конечное потребление продукции I-й отрасли увеличится на 22%, а II-й отрасли уменьшится на 10%.
2.90.Для задачи 2.88 найти необходимый объем валового выпуска отрасли, если конечное потребление продукции I-й отрасли увеличится на 20%, II-й отрасли уменьшится на 18%, а III-й отрасли увеличится на 15%.

Г л а в а 3
Векторы на плоскости и в пространстве
§ 3.1. Векторы. Линейные операции над векторами
Вектор (в пространстве, на плоскости, на прямой) — это направленный отрезок, т. е. отрезок , взятый с одним из двух возможных
направлений: от к или от к . Итак, с отрезком связаны
|
и |
|
. |
|
|
|
|
||
два вектора: −−→ |
|
−−→ |
называется длиной, или модулем, вектора |
||||||
|
Длина отрезка |
|
|
||||||
|
|
|
|
|
|
|
−−→ |
||
и обозначается |
|
. |
|
|
|
|
|||
|
|
|−−→| |
|
|
|
|
|
||
|
Вектор, длина которого равна нулю, называется нулевым векто- |
||||||||
ром |
и обозначается |
|
0 . Вектор, длина которого равна единице, назы- |
||||||
|
→− |
|
|
|
|
||||
вается единичным вектором, или ортом. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Пусть и — два произвольных вектора. Не теряя общности, |
||||||||
предположим, что |
|
|
|
|
|
|
|
||
|
|
и = . Вектор называется суммой |
|||||||
|
|
|
= −→ |
|
−−→ |
−−→ |
|||
|
|
|
|
|
|
|
|
|
|
векторов и и обозначается + (рис. 3.1).
Рис. 3.1
Произведением вектора на число называется вектор, обозначаемый , длина которого равна числу | | · | |, а направление совпадает с направлением вектора , если > 0, и имеет противоположное направление (т. е. направлением вектора − ), если < 0.
§ 3.1. Векторы. Линейные операции над векторами |
69 |
|
|
|
|
|
|
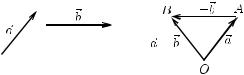
Вектор (−1) · называется противоположным по отношению к |
|||
вектору |
|
|
|
и обозначается − , а разность − определяется как +(− ) |
|||
(рис. 3.2).
Рис. 3.2
Выражение + , где , — произвольные постоянные, назы-
вается линейной комбинацией векторов и .
3.1. Доказать, что операция сложения векторов имеет следующие основные свойства:
1.+ = + (свойство коммутативности ),
2.( + ) + = + ( + ) (свойство ассоциативности ),
|
|
3. |
|
|
= |
(свойство существования нулевого вектора), |
|
|||
|
|
|
+ 0 |
|
|
|||||
|
|
4. |
|
|
|
|
|
|
(свойство существования противоположного |
|
|
|
|
+(− ) = 0 |
|
||||||
вектора). |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 , |
|
|
3.2. Даны ненулевые векторы и . Построить векторы |
||||||||
− |
3 |
, − |
|
1 |
|
|
1 |
|
|
|
2 |
2 |
|
, |
3 |
+ 3 . |
|
||||
3.3. Доказать, что операция произведения вектора на число имеет следующие основные свойства:
1.( ) = ( ) (свойство ассоциативности ),
2.( + ) = + (свойство дистрибутивности относительно суммы векторов),
3.( + ) = + (свойство дистрибутивности относительно суммы чисел).
70 |
|
|
Глава 3. Векторы на плоскости и в пространстве |
||||||||
|
|
|
|
|
|||||||
|
3.4. Доказать равенства: |
|
|||||||||
|
|
|
1 |
|
|
1 |
|
|
|
||
|
а) + |
2 |
( − ) = |
2 |
( + ), |
||||||
|
|
|
1 |
|
|
1 |
|
|
|
||
|
б) − |
2 |
( + ) = |
2 |
( − ). |
||||||
|
Объяснить их геометрический смысл. |
||||||||||
|
3.5. На сторонах и прямоугольника отложе- |
||||||||||
|
|
|
|
|
1 |
−−→ |
|
|
|
1 |
−−→ |
|
ны векторы = |
|
и = |
3 |
. Выразить через векторы и |
||||||
|
|
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
следующие векторы: |
|
|
|
|
||||||
|
а) |
−−→ −−→ −−→ −−→ |
|
|
|
||||||
|
|
, , , , |
|
|
|
||||||
|
б) |
−→ −→ −−→ −−→ |
|
|
|
||||||
|
|
, , , . |
|
|
|
||||||
|
|
|
−−→ |
|
|
−→ |
3.6. Векторы = и = построены на сторонах |
||||||
|
|
|
|
|
−−→ −→ −−→ −−→ |
|
треугольника |
|
|
. Представить векторы , , , в |
|||
|
|
|
|
|
|
|
виде линейной комбинации векторов и . |
||||||
3.7. Векторы |
= −−→ |
|
|
−−→ |
||
|
и = построены на сторонах па- |
|||||
раллелограмма , является точкой пересечения диаго- |
|||||
налей. Представить векторы |
−→ −→ −−→ −−→ |
|
|
||
|
|
, , , в виде линейной |
|||
|
|
|
|
|
|
комбинации векторов и . |
|
|
|
−→ |
|
|
|
|
|
= |
|
|
3.8. В параллелограмме |
|
даны векторы |
|
и |
= −−→ |
|
|
|
|
|
|
, где — точка пересечения диагоналей. Представить |
||||
векторы −−→ −−→ −−→ −−→ −→ |
|
|
|
||
|
, , , , в виде линейной комбинации |
||||
|
|
|
|
|
|
векторов и . |
|
|
|
|
|
|
3.9. Точки 1, 2 и 3 делят сторону треугольника |
||||
ABC на четыре равные части. Представить векторы |
−−→ −−→ |
||||
−→ |
|
|
−−→1 |
, и |
|
|
|
|
−−→2 |
||
в виде линейной комбинации векторов = |
и = . |
||||
3.10. Точка — пересечение диагоналей параллелограмма
.
а) Представить б) Представить в) Представить
−−→ |
−−→ |
−−→ |
в виде линейной комбинации и . |
||
−−→ |
−−→ |
−−→ |
в виде линейной комбинации и . |
||
−−→ |
−→ |
−−→ |
в виде линейной комбинации и .
