
- •Основы теории электромагнитного поля
- •Оглавление
- •Введение
- •1. Общие сведения о теории электромагнитного поля
- •1.1. Понятие поля. Скалярные и векторные поля
- •1.2.Основные векторные величины, характеризующие электромагнитное поле
- •1.3. Виды плотности тока
- •1.4.Основные уравнения Максвелла и их физический смысл
- •1.4.1.Закон полного тока
- •1.4.2. Закон электромагнитной индукции
- •1.4.3. Принцип непрерывности магнитной индукции
- •1.4.4. Теорема Гаусса (постулат Максвелла)
- •1.4.5. Система уравнений Максвелла
- •1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга
- •1.6.Частные виды электромагнитных полей
- •Вопросы для самопроверки
- •2.Электростатическое поле
- •2.1. Закон Кулона
- •2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •2.3. Электрический потенциал
- •2.4.Картина поля.
- •2.5.Потенциал заданного распределения заряда
- •2.5.1.Потенциал и напряженность электрического поля диполя
- •2.6.Уравнение Пуассона и Лапласа
- •2.7. Поляризация вещества. Вектор поляризации
- •2.8.Проводники в электростатическом поле. Электростатическое экранирование
- •2.9. Граничные условия в электростатическом поле
- •2.9.1.Граничные условия для составляющих векторов поля.
- •2.9.2.Граничные условия для потенциала
- •2.10.Теорема единственности решения
- •2.11.Электрическая емкость
- •2.12. Энергия электростатического поля
- •2.13. Силы, действующие в электростатическом поле
- •2.14.Расчет электростатических полей
- •2.14.1. Поле уединенной равномерно заряженной оси
- •2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей
- •2.14.3.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров (двухпроводной линии)
- •2.14.4.Поле и емкость между несосными, охватывающими друг друга круглыми цилиндрами
- •2.14.5.Поле и емкость системы "цилиндр – плоскость"
- •2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)
- •2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)
- •2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости
- •2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
- •2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли
- •2.14.11. Электрическое поле и емкость трехфазной линии электропередачи
- •2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией
- •2. Находим напряженность электрического поля как .
- •2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле
- •3. Электрическое поле постоянного тока
- •3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами
- •3.2.Электрическое поле постоянного тока в проводящей среде
- •3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
- •3.2.2.Граничные условия на поверхности раздела двух проводящих сред
- •3.2.3. Методы расчета электрических полей постоянного тока
- •3.4.Задачи Задача 1
- •Задача 2. Расчет тока утечки между двумя жилами коаксиального кабеля
- •Задача 3. Заземлитель в виде шара
- •Задача 4.
- •Вопросы для самопроверки
- •4. Магнитное поле постоянных токов
- •4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •4. 2. Векторный потенциал магнитного поля
- •4.3. Выражение магнитного потока и энергии через векторный потенциал
- •4.4.Граничные условия в магнитном поле
- •4.3.1. Граничные условия для векторного потенциала магнитного поля
- •4.3. Скалярный потенциал магнитного поля
- •4.3. Магнитное поле цилиндрического проводника с током
- •4.4.Магнитное поле коаксиального кабеля
- •4.5. Поток вектора Пойтинга в коаксиальном кабеле
- •4.6. Магнитное поле и индуктивность двухпроводной линии
- •4.7. Взаимная индуктивность двух параллельных линий
- •4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током
- •4.9. Графический метод построения картины поля
- •4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Методзеркальных изображений
- •4.11.Магнитное экранирование
- •Вопросы для самопроверки
- •5. Переменное электромагнитное поле
- •5.1. Уравнения Максвелла в комплексной форме
- •5.2 Плоская гармоническая волна в диэлектрике
- •5.3. Плоская гармоническая волна в проводящей среде
- •5.4. Магнитный поверхностный эффект в плоском листе
- •5.5.Электрический поверхностный эффект
- •5.6.Эффект близости
- •5.7. Поверхностный эффект в круглом проводе
- •5.8. Экранирование в переменном магнитном поле
- •5.9.Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
- •5.10. Излучение электромагнитной энергии
- •Вопросы для самопроверки
- •Приложение Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат
- •Литература
2.7. Поляризация вещества. Вектор поляризации
Свободными называются заряды, которые под воздействием сил поля могут свободно перемещаться в веществе, их перемещение не ограничено внутримолекулярными силами. Связанными называют заряды, входящие в состав вещества и удерживаемые в определенных положениях внутримолекулярными силами. Эти заряды связаны с самим веществом и неотделимы от него.
Напряженность электрического поля уменьшается. Изменение напряженности электрического поля в диэлектрике вызывается поляризацией диэлектрика.
Диэлектрики делятся на две группы. В первую группу входят диэлектрики, состоящие из неполярных молекул, во вторую – диэлектрики, состоящие из полярных молекул (диполей).
Диполем
называют совокупность двух равных
зарядов противоположного знака,
находящихся друг от друга на расстоянии
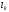 ,
малом по сравнению с расстоянием до
точек, в которых определяется напряженность
электрического поля (рис.2.2). Диполь
характеризуется электрическим моментом.
,
малом по сравнению с расстоянием до
точек, в которых определяется напряженность
электрического поля (рис.2.2). Диполь
характеризуется электрическим моментом.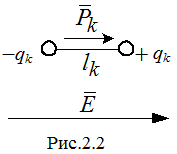
Электрическим
моментом диполя
 называется произведение зарядаqk
и плеча диполя
называется произведение зарядаqk
и плеча диполя
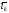 –
вектор, направленный от отрицательного
заряда к положительному, длина которого
равна расстоянию между зарядами, т. е.
–
вектор, направленный от отрицательного
заряда к положительному, длина которого
равна расстоянию между зарядами, т. е.
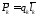 .
.
Для
молекул
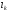 – это расстояние, на которое центр
тяжести отрицательного заряда смещается
относительно центра тяжести положительного
заряда.
– это расстояние, на которое центр
тяжести отрицательного заряда смещается
относительно центра тяжести положительного
заряда.
Под действием внешнего электрического поля все неполярные (нейтральные) молекулы диэлектрика превращаются в диполи, которые стремятся ориентироваться в пространстве таким образом, чтобы их электрические моменты были направлены по вектору напряженности электрического поля (рис. 2.2). Это явление и называют поляризацией диэлектриков первой группы.
Молекулы диэлектриков второй группы представляют собой диполи даже при отсутствии внешнего поля. Именно поэтому их называют полярными. Благодаря тепловому движению диполи располагаются хаотично, так что при отсутствии внешнего электрического поля их электрические поля взаимно нейтрализуются. Под действием внешнего поля полярные молекулы (диполи) ориентируются по направлению вектора его напряженности. Так происходит поляризация диэлектриков второй группы.
Поляризацией называется процесс появления под действием электрического поля ориентированных по полю диполей.
Для
характеристики поляризации используют
вектор поляризации
 .
.
Вектором
поляризации
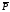 называют электрический момент единицы
объема,
называют электрический момент единицы
объема,
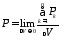 ,
,
где
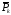 – электрический момент диполя молекулы;
– электрический момент диполя молекулы;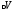 – физически малый объем;n
– количество диполей в объеме
– физически малый объем;n
– количество диполей в объеме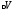 .
Электрический момент единицы объема,
в отличие от момента одной молекулы или
пары молекул, является макроскопической
характеристикой процесса поляризации.
.
Электрический момент единицы объема,
в отличие от момента одной молекулы или
пары молекул, является макроскопической
характеристикой процесса поляризации.
Для
однородных и изотропных диэлектриков
в относительно слабых полях вектор
поляризации
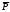 пропорционален напряженности
электрического поля,
пропорционален напряженности
электрического поля,
 ,
(2.6)
,
(2.6)
где
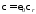 – абсолютная диэлектрическая
восприимчивость среды;
– абсолютная диэлектрическая
восприимчивость среды;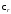 – относительная восприимчивость среды,
– относительная восприимчивость среды,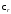 связана с
связана с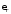 соотношением
соотношением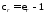 ,
подставляя которое в уравнение (2.6),
получим
,
подставляя которое в уравнение (2.6),
получим
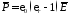 .
.
Вектор
электрической индукции связан с векторами
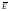 и
и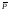 следующим образом:
следующим образом:
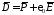 .
.
Вернемся
к поляризации диэлектриков. Внесем
пластину из диэлектрика в однородное
электрическое поле
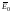 (рис. 2.3).
(рис. 2.3).
В результате поляризации на торцах появляются так называемые нескомпенсированные (избыточные) связанные заряды: на одной торцевой поверхности – отрицательный заряд, на другой – положительный. Связанные
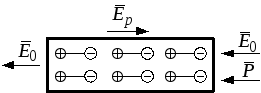
Рис. 2.3
заряды
создают свое поле, напряженность
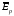 которого направлена против напряженности
внешнего поля
которого направлена против напряженности
внешнего поля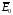 .
Напряженность результирующего поля
(поля внутри диэлектрика)
.
Напряженность результирующего поля
(поля внутри диэлектрика)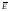 уменьшается по сравнению с
уменьшается по сравнению с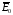 :
:
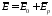 ,
,
 .
.
Математически процесс поляризации диэлектриков описывается соотношением, аналогичным теореме Гаусса.
Поток
вектора поляризации
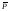 сквозь произвольную замкнутую поверхность
сквозь произвольную замкнутую поверхность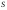 равен взятой с обратным знаком
алгебраической сумме нескомпенсированных
(избыточных) связанных зарядов, находящихся
в объеме, ограниченном этой поверхностью:
равен взятой с обратным знаком
алгебраической сумме нескомпенсированных
(избыточных) связанных зарядов, находящихся
в объеме, ограниченном этой поверхностью:
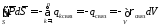 , (2.7)
, (2.7)
где
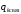 –k-й дискретный
нескомпенсированный связанный заряд,
расположенный внутри объема
–k-й дискретный
нескомпенсированный связанный заряд,
расположенный внутри объема
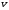 ;
; – полный (суммарный) связанный заряд
внутри объема;
– полный (суммарный) связанный заряд
внутри объема;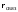 – объемная плотность избыточного
связанного заряда (для случая его
непрерывного распределения),
– объемная плотность избыточного
связанного заряда (для случая его
непрерывного распределения),
 .
.
Соответствующая дифференциальная форма закона (2.7) имеет вид
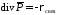 .
(2.8)
.
(2.8)
Физическое
и геометрическое содержания (2.7) и (2.8)
заключаются в следующем: источниками
вектора
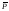 являются связанные заряды; линии вектора
являются связанные заряды; линии вектора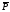 начинаются и заканчиваются насвязанных
зарядах.
начинаются и заканчиваются насвязанных
зарядах.
Можно
получить обобщенное выражение для
напряженности электрического поля
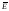
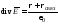 .
(2.9)
.
(2.9)
Физический
смысл выражения (2.9): источниками вектора
 являются как свободные, так и связанные
заряды. Геометрическое содержание
(2.9): линии вектора
являются как свободные, так и связанные
заряды. Геометрическое содержание
(2.9): линии вектора начинаются и заканчиваются насвободных
и связанных
зарядах.
начинаются и заканчиваются насвободных
и связанных
зарядах.
