
- •Основы теории электромагнитного поля
- •Оглавление
- •Введение
- •1. Общие сведения о теории электромагнитного поля
- •1.1. Понятие поля. Скалярные и векторные поля
- •1.2.Основные векторные величины, характеризующие электромагнитное поле
- •1.3. Виды плотности тока
- •1.4.Основные уравнения Максвелла и их физический смысл
- •1.4.1.Закон полного тока
- •1.4.2. Закон электромагнитной индукции
- •1.4.3. Принцип непрерывности магнитной индукции
- •1.4.4. Теорема Гаусса (постулат Максвелла)
- •1.4.5. Система уравнений Максвелла
- •1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга
- •1.6.Частные виды электромагнитных полей
- •Вопросы для самопроверки
- •2.Электростатическое поле
- •2.1. Закон Кулона
- •2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •2.3. Электрический потенциал
- •2.4.Картина поля.
- •2.5.Потенциал заданного распределения заряда
- •2.5.1.Потенциал и напряженность электрического поля диполя
- •2.6.Уравнение Пуассона и Лапласа
- •2.7. Поляризация вещества. Вектор поляризации
- •2.8.Проводники в электростатическом поле. Электростатическое экранирование
- •2.9. Граничные условия в электростатическом поле
- •2.9.1.Граничные условия для составляющих векторов поля.
- •2.9.2.Граничные условия для потенциала
- •2.10.Теорема единственности решения
- •2.11.Электрическая емкость
- •2.12. Энергия электростатического поля
- •2.13. Силы, действующие в электростатическом поле
- •2.14.Расчет электростатических полей
- •2.14.1. Поле уединенной равномерно заряженной оси
- •2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей
- •2.14.3.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров (двухпроводной линии)
- •2.14.4.Поле и емкость между несосными, охватывающими друг друга круглыми цилиндрами
- •2.14.5.Поле и емкость системы "цилиндр – плоскость"
- •2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)
- •2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)
- •2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости
- •2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
- •2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли
- •2.14.11. Электрическое поле и емкость трехфазной линии электропередачи
- •2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией
- •2. Находим напряженность электрического поля как .
- •2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле
- •3. Электрическое поле постоянного тока
- •3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами
- •3.2.Электрическое поле постоянного тока в проводящей среде
- •3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
- •3.2.2.Граничные условия на поверхности раздела двух проводящих сред
- •3.2.3. Методы расчета электрических полей постоянного тока
- •3.4.Задачи Задача 1
- •Задача 2. Расчет тока утечки между двумя жилами коаксиального кабеля
- •Задача 3. Заземлитель в виде шара
- •Задача 4.
- •Вопросы для самопроверки
- •4. Магнитное поле постоянных токов
- •4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •4. 2. Векторный потенциал магнитного поля
- •4.3. Выражение магнитного потока и энергии через векторный потенциал
- •4.4.Граничные условия в магнитном поле
- •4.3.1. Граничные условия для векторного потенциала магнитного поля
- •4.3. Скалярный потенциал магнитного поля
- •4.3. Магнитное поле цилиндрического проводника с током
- •4.4.Магнитное поле коаксиального кабеля
- •4.5. Поток вектора Пойтинга в коаксиальном кабеле
- •4.6. Магнитное поле и индуктивность двухпроводной линии
- •4.7. Взаимная индуктивность двух параллельных линий
- •4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током
- •4.9. Графический метод построения картины поля
- •4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Методзеркальных изображений
- •4.11.Магнитное экранирование
- •Вопросы для самопроверки
- •5. Переменное электромагнитное поле
- •5.1. Уравнения Максвелла в комплексной форме
- •5.2 Плоская гармоническая волна в диэлектрике
- •5.3. Плоская гармоническая волна в проводящей среде
- •5.4. Магнитный поверхностный эффект в плоском листе
- •5.5.Электрический поверхностный эффект
- •5.6.Эффект близости
- •5.7. Поверхностный эффект в круглом проводе
- •5.8. Экранирование в переменном магнитном поле
- •5.9.Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
- •5.10. Излучение электромагнитной энергии
- •Вопросы для самопроверки
- •Приложение Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат
- •Литература
2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
Для электростатического поля имеем:
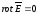 или
или
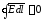 .
.
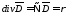 или
или
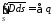 ,
,
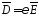 .
.
Ротор
вектора
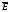 характеризует его вихри в пространстве.
Равенство
характеризует его вихри в пространстве.
Равенство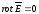 означает, чтоэлектростатическое
поле является безвихревым, т.е.
потенциальным.
означает, чтоэлектростатическое
поле является безвихревым, т.е.
потенциальным.
В
декартовой системе координат операция
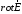 записыватся
так:
записыватся
так:
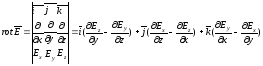 .
.
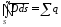 интегральная
форма записи теоремы Гаусса в обобщенной
форме гласит, что поток
вектора электрического смещения
интегральная
форма записи теоремы Гаусса в обобщенной
форме гласит, что поток
вектора электрического смещения
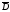 сквозь замкнутую поверхностьS
равен алгебраической сумме свободных
зарядов, расположенные внутри поверхности
S.
сквозь замкнутую поверхностьS
равен алгебраической сумме свободных
зарядов, расположенные внутри поверхности
S.
Для
однородной среды
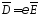 ,
тогда
,
тогда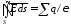 .
.
По теореме Остроградского перейдем к дифференциальной форме уравнения теоремы Гаусса:
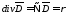 ―дифференциальная
форма теоремы Гаусса.
―дифференциальная
форма теоремы Гаусса.
Дивергенция
вектора
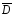 характеризует его истоки в пространстве,
следовательно, линии вектора
характеризует его истоки в пространстве,
следовательно, линии вектора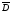 начинаются на положительных зарядах и
заканчиваются на отрицательных.
начинаются на положительных зарядах и
заканчиваются на отрицательных.
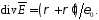
Истоком
вектора
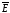 в отличие от истока вектора
в отличие от истока вектора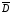 являются не только свободныеρ,
но и связанные заряды
являются не только свободныеρ,
но и связанные заряды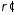 .
.
В декартовой системе координат операция div запишется так:
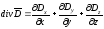 .
.
Для
однородной среды
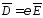 ,
тогда
,
тогда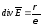 .
.
2.3. Электрический потенциал
Равенство
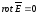 означает, что электростатическое
поле является безвихревым, т.е.
потенциальным.
Учитывая,
что
означает, что электростатическое
поле является безвихревым, т.е.
потенциальным.
Учитывая,
что
 ,
,
приходим
к следующему выводу, что для
электростатического поля можно найти
некоторую скалярную функцию
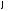 такую, что
такую, что
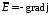 .
(2.1)
.
(2.1)
Скалярная
функция
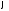 называетсяпотенциальной
функцией, или просто потенциалом.
называетсяпотенциальной
функцией, или просто потенциалом.
Потенциал можно выразить через напряженность электростатического поля с точностью до постоянной:
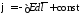 .
(2.2)
.
(2.2)
Запишем формулу, определяющую напряжение между двумя произвольными точками поля а и p:
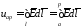 .
(2.3)
.
(2.3)
Напряжение между двумя произвольными точками равно работе (энергии), затраченной полем на перемещение единичного положительного заряда из одной точки в другую.
В потенциальном поле напряжение равно разности потенциалов.
Полагая
потенциал некоторой фиксированной
точки p поля равным
нулю (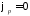 ),
получим:
),
получим:
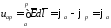 .
.
Потенциал некоторой точки есть работа (энергия), затрачиваемая полем на перемещение единичного положительного заряда из данной точки в фиксированную точку, где потенциал принят равным нулю
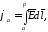
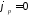 .
(2.4)
.
(2.4)
В электротехнике за базовую точку с заданным нулевым потенциалом принимают “землю”, а при отсутствии заземления любую точку.
Потенциал является энергетической характеристикой поля.
Напряженность электрического поля определяется как градиент потенциала
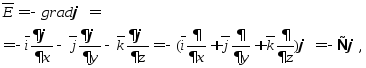
где
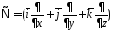
оператор пространственного
дифференцирования.
оператор пространственного
дифференцирования.
2.4.Картина поля.
Электрическое поле можно наглядно характеризовать совокупностью силовых и эквипотенциальных линий.
Силовая
линия – это мысленно проведенная в поле
линия, начинающаяся на отрицательно
заряженном теле. Проводится она таким
образом, что касательная к ней в любой
точке ее дает направление напряженности
поля
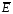 в этой точке. Вдоль силовой линии
передвигался бы весьма малый положительный
заряд, если бы он имел возможность
свободно перемещаться в поле и если бы
он не обладал инерцией.
в этой точке. Вдоль силовой линии
передвигался бы весьма малый положительный
заряд, если бы он имел возможность
свободно перемещаться в поле и если бы
он не обладал инерцией.
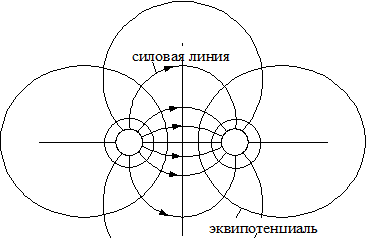
В электрическом поле могут быть проведены эквипотенциальные (равнопотенциальные) поверхности. Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал. Если мысленно рассечь электростатическое поле какой-либо секущей плоскостью, то в полученном сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Их называют эквипотенциальными линиями (или эквипотенциалями).
Эквипотенциальные и силовые линии в любой точке поля пересекаются под прямым углом. На рисунке для примера изображены два заряженных тела и проведено несколько силовых и эквипотенциальных линий.
