
- •Основы теории электромагнитного поля
- •Оглавление
- •Введение
- •1. Общие сведения о теории электромагнитного поля
- •1.1. Понятие поля. Скалярные и векторные поля
- •1.2.Основные векторные величины, характеризующие электромагнитное поле
- •1.3. Виды плотности тока
- •1.4.Основные уравнения Максвелла и их физический смысл
- •1.4.1.Закон полного тока
- •1.4.2. Закон электромагнитной индукции
- •1.4.3. Принцип непрерывности магнитной индукции
- •1.4.4. Теорема Гаусса (постулат Максвелла)
- •1.4.5. Система уравнений Максвелла
- •1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга
- •1.6.Частные виды электромагнитных полей
- •Вопросы для самопроверки
- •2.Электростатическое поле
- •2.1. Закон Кулона
- •2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •2.3. Электрический потенциал
- •2.4.Картина поля.
- •2.5.Потенциал заданного распределения заряда
- •2.5.1.Потенциал и напряженность электрического поля диполя
- •2.6.Уравнение Пуассона и Лапласа
- •2.7. Поляризация вещества. Вектор поляризации
- •2.8.Проводники в электростатическом поле. Электростатическое экранирование
- •2.9. Граничные условия в электростатическом поле
- •2.9.1.Граничные условия для составляющих векторов поля.
- •2.9.2.Граничные условия для потенциала
- •2.10.Теорема единственности решения
- •2.11.Электрическая емкость
- •2.12. Энергия электростатического поля
- •2.13. Силы, действующие в электростатическом поле
- •2.14.Расчет электростатических полей
- •2.14.1. Поле уединенной равномерно заряженной оси
- •2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей
- •2.14.3.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров (двухпроводной линии)
- •2.14.4.Поле и емкость между несосными, охватывающими друг друга круглыми цилиндрами
- •2.14.5.Поле и емкость системы "цилиндр – плоскость"
- •2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)
- •2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)
- •2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости
- •2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
- •2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли
- •2.14.11. Электрическое поле и емкость трехфазной линии электропередачи
- •2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией
- •2. Находим напряженность электрического поля как .
- •2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле
- •3. Электрическое поле постоянного тока
- •3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами
- •3.2.Электрическое поле постоянного тока в проводящей среде
- •3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
- •3.2.2.Граничные условия на поверхности раздела двух проводящих сред
- •3.2.3. Методы расчета электрических полей постоянного тока
- •3.4.Задачи Задача 1
- •Задача 2. Расчет тока утечки между двумя жилами коаксиального кабеля
- •Задача 3. Заземлитель в виде шара
- •Задача 4.
- •Вопросы для самопроверки
- •4. Магнитное поле постоянных токов
- •4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •4. 2. Векторный потенциал магнитного поля
- •4.3. Выражение магнитного потока и энергии через векторный потенциал
- •4.4.Граничные условия в магнитном поле
- •4.3.1. Граничные условия для векторного потенциала магнитного поля
- •4.3. Скалярный потенциал магнитного поля
- •4.3. Магнитное поле цилиндрического проводника с током
- •4.4.Магнитное поле коаксиального кабеля
- •4.5. Поток вектора Пойтинга в коаксиальном кабеле
- •4.6. Магнитное поле и индуктивность двухпроводной линии
- •4.7. Взаимная индуктивность двух параллельных линий
- •4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током
- •4.9. Графический метод построения картины поля
- •4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Методзеркальных изображений
- •4.11.Магнитное экранирование
- •Вопросы для самопроверки
- •5. Переменное электромагнитное поле
- •5.1. Уравнения Максвелла в комплексной форме
- •5.2 Плоская гармоническая волна в диэлектрике
- •5.3. Плоская гармоническая волна в проводящей среде
- •5.4. Магнитный поверхностный эффект в плоском листе
- •5.5.Электрический поверхностный эффект
- •5.6.Эффект близости
- •5.7. Поверхностный эффект в круглом проводе
- •5.8. Экранирование в переменном магнитном поле
- •5.9.Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
- •5.10. Излучение электромагнитной энергии
- •Вопросы для самопроверки
- •Приложение Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат
- •Литература
1.6.Частные виды электромагнитных полей
1.Статические поля:
электростатическое поле - создается неподвижными заряженными телами;
магнитостатические поля - поля постоянных магнитов.
2.Стационарные поля:
2.1.Электрическое
поле постоянного тока
(стационарное электрическое поле)
образуется внутри и вне проводников
при прохождении по ним постоянного
тока. При этом внутри однородного
проводника отсутствует объемная
плотность заряда, т.е. div  = 0.
= 0.
2.2.Магнитное поле постоянного магнитного потока.
Магнитное поле постоянного потока и электрическое поле постоянного тока могут рассматриваться независимо друг от друга.
3.Квазистационарные
поля ( ).
).
4.Общий случай.
Вопросы для самопроверки
Объясните физический смысл уравнений Максвелла.
2.Какой формулой может выражаться индукция магнитного поля?
а) B=iB0e-αx ; б) B=iax+jby; в) B=iax ; г) B=iax-jby;
где: i, j-орты осей.
3.Под индукцией В, входящей в правую часть второго уравнения Максвелла следует понимать:
а) индукцию стороннего поля; б) индукцию индуцированного поля;
в) индукцию токов электрического смещения;
г) индукцию от стороннего и индуктированного полей.
4. Отсутствие магнитных зарядов в природе следует из формулы:
 ;
б)
;
б)
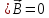 ;
с)
;
с) ;
г)
;
г) ;
;
4.Закон электромагнитной индукции в интегральной форме:
а)
 ;
б)
;
б) ;
;
с)
 ;
г)
;
г) .
.
5.div(B/μ0) равна:
а) плотности молекулярных токов jм;
б) плотности тока проводимости j;
в) j+jм;
г) 0.
6.Теорема Гаусса в дифференциальной форме имеет вид …
а) divB=0; б;) div H=0; в) divD=ρ; г) rotH=0.
7.Стационарное магнитное поле – поле, создаваемое …
1) постоянными токами;
2) электрическими зарядами любого вида;
3) постоянными зарядами и токами;
4) неизменными во времени неподвижными зарядами.
8. divD равна:
а) объемной плотности связанных зарядов ρсв ;
б) объемной плотности свободных зарядов ρ;
в) ρ+ρсв ;
г) поверхностной плотности свободных зарядов.
2.Электростатическое поле
Электростатическое поле представляет собой частный вид электромагнитного поля. Оно создается совокупностью электрических зарядов неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.
Электростатическому полю присуща способность воздействвать на помещенный в него электрический заряд с механической силой, прямо пропорциональной величине этого заряда.
2.1. Закон Кулона
Электростатическое поле – это поле, не изменяющееся во времени. Электростатическое поле является частным случаем электромагнитного поля. Электростатическое поле создается совокупностью электрических зарядов, неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.
Основным законом электростатики является закон Кулона, математически определяющий силу взаимодействия двух неподвижных точечных зарядов.
Закон Кулона: между двумя покоящимися точечными зарядами q1 и q2 действует сила, прямо пропорциональная произведению зарядов и обратно пропорциональная квадрату расстояния между ними. Сила направлена по прямой от одного заряда к другому.

где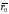 – единичный вектор, направленный по
прямой от положительного заряда к
отрицательному заряду;r
– расстояние между зарядами.
– единичный вектор, направленный по
прямой от положительного заряда к
отрицательному заряду;r
– расстояние между зарядами.
Напряженность электростатического поля можно определить как силу, действующую на единицу заряда.
По закону Кулона можно определить величину напряженности электростатического поля, создаваемого уединенным точечным телом с зарядом q в некоторой точке, отстоящей от этого тела на расстоянии r:
 .
.
Здесь εr – относительная диэлектрическая проницаемость среды;
 (Ф/м)-
электрическая постоянная;
(Ф/м)-
электрическая постоянная;
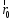 единичный
радиус-вектор, направленный по радиусу
от заряда, если q
>
0, и к заряду, если q<0.
единичный
радиус-вектор, направленный по радиусу
от заряда, если q
>
0, и к заряду, если q<0.

В линейных средах выполняется принцип наложения.
Принцип наложения (суперпозиции): если поле создается несколькими точечными зарядами, то общая напряженность электрического поля в любой точке равна геометрической сумме напряженностей от каждого заряда в отдельности,
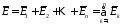 ,
,

где
 – напряженности в заданной точке,
возбуждаемые точечными зарядами
– напряженности в заданной точке,
возбуждаемые точечными зарядами (рис. 2.1). Длина вектора
(рис. 2.1). Длина вектора определяется по формуле
определяется по формуле
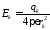 .
.
Если электростатическое поле создается системой распределенных в пространстве зарядов, то эти заряды разбиваются на элементарные точечные заряды dq, а операция сложения заменяется интегрированием по объему, площади или длине, в зависимости от того, как распределены заряды в пространстве.
