
- •Основы теории электромагнитного поля
- •Оглавление
- •Введение
- •1. Общие сведения о теории электромагнитного поля
- •1.1. Понятие поля. Скалярные и векторные поля
- •1.2.Основные векторные величины, характеризующие электромагнитное поле
- •1.3. Виды плотности тока
- •1.4.Основные уравнения Максвелла и их физический смысл
- •1.4.1.Закон полного тока
- •1.4.2. Закон электромагнитной индукции
- •1.4.3. Принцип непрерывности магнитной индукции
- •1.4.4. Теорема Гаусса (постулат Максвелла)
- •1.4.5. Система уравнений Максвелла
- •1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга
- •1.6.Частные виды электромагнитных полей
- •Вопросы для самопроверки
- •2.Электростатическое поле
- •2.1. Закон Кулона
- •2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •2.3. Электрический потенциал
- •2.4.Картина поля.
- •2.5.Потенциал заданного распределения заряда
- •2.5.1.Потенциал и напряженность электрического поля диполя
- •2.6.Уравнение Пуассона и Лапласа
- •2.7. Поляризация вещества. Вектор поляризации
- •2.8.Проводники в электростатическом поле. Электростатическое экранирование
- •2.9. Граничные условия в электростатическом поле
- •2.9.1.Граничные условия для составляющих векторов поля.
- •2.9.2.Граничные условия для потенциала
- •2.10.Теорема единственности решения
- •2.11.Электрическая емкость
- •2.12. Энергия электростатического поля
- •2.13. Силы, действующие в электростатическом поле
- •2.14.Расчет электростатических полей
- •2.14.1. Поле уединенной равномерно заряженной оси
- •2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей
- •2.14.3.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров (двухпроводной линии)
- •2.14.4.Поле и емкость между несосными, охватывающими друг друга круглыми цилиндрами
- •2.14.5.Поле и емкость системы "цилиндр – плоскость"
- •2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)
- •2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)
- •2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости
- •2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
- •2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли
- •2.14.11. Электрическое поле и емкость трехфазной линии электропередачи
- •2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией
- •2. Находим напряженность электрического поля как .
- •2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле
- •3. Электрическое поле постоянного тока
- •3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами
- •3.2.Электрическое поле постоянного тока в проводящей среде
- •3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
- •3.2.2.Граничные условия на поверхности раздела двух проводящих сред
- •3.2.3. Методы расчета электрических полей постоянного тока
- •3.4.Задачи Задача 1
- •Задача 2. Расчет тока утечки между двумя жилами коаксиального кабеля
- •Задача 3. Заземлитель в виде шара
- •Задача 4.
- •Вопросы для самопроверки
- •4. Магнитное поле постоянных токов
- •4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •4. 2. Векторный потенциал магнитного поля
- •4.3. Выражение магнитного потока и энергии через векторный потенциал
- •4.4.Граничные условия в магнитном поле
- •4.3.1. Граничные условия для векторного потенциала магнитного поля
- •4.3. Скалярный потенциал магнитного поля
- •4.3. Магнитное поле цилиндрического проводника с током
- •4.4.Магнитное поле коаксиального кабеля
- •4.5. Поток вектора Пойтинга в коаксиальном кабеле
- •4.6. Магнитное поле и индуктивность двухпроводной линии
- •4.7. Взаимная индуктивность двух параллельных линий
- •4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током
- •4.9. Графический метод построения картины поля
- •4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Методзеркальных изображений
- •4.11.Магнитное экранирование
- •Вопросы для самопроверки
- •5. Переменное электромагнитное поле
- •5.1. Уравнения Максвелла в комплексной форме
- •5.2 Плоская гармоническая волна в диэлектрике
- •5.3. Плоская гармоническая волна в проводящей среде
- •5.4. Магнитный поверхностный эффект в плоском листе
- •5.5.Электрический поверхностный эффект
- •5.6.Эффект близости
- •5.7. Поверхностный эффект в круглом проводе
- •5.8. Экранирование в переменном магнитном поле
- •5.9.Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
- •5.10. Излучение электромагнитной энергии
- •Вопросы для самопроверки
- •Приложение Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат
- •Литература
4.4.Магнитное поле коаксиального кабеля
По кабелю замыкается ток I. Рассчитать поле и индуктивность коаксиального кабеля.
Снаружи кабеля поле отсутствует, так как I = 0.
Таким образом, можно выделить три различные области с магнитными проницаемостями 1, 2, 3.
Для
расчета поля используем закон полного
тока:
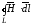 =I.
=I.
1. Область
I – 0 < r
< r1:
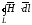 =H·2r;
=H·2r;
I=I
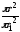 ;H=
;H= ·r;B=1·H=
·r;B=1·H=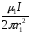 ·r;dФ=B·dS=
·r;dФ=B·dS= ·r·l·dr.
·r·l·dr.
Так как
во внутреннем проводнике магнитный
поток dФ
сцеплен только с частью тока I,
которая пропорциональна отношению
r2/r12,
то магнитное потокосцепление d
= dФ·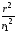 .
.
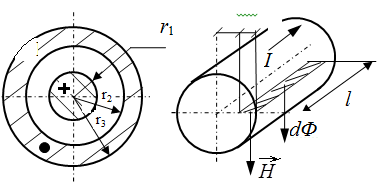
Рис.4.5
Внутренняя индуктивность первой области вычисляется по формуле
l1
= =
=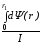 =
=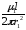 ·
·
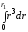 =
=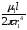 ·
·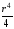
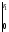 =
=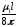
и, как видим, не зависит от радиуса жилы.
2. Область II – r1 < r < r2.
I=I;H= ;B=
;B= ;d=dФ=B·dS=
;d=dФ=B·dS=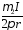 ·l·dr.
·l·dr.
внешняя
индуктивность l2
=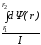 =
=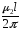 ln
ln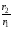 .
.
3. Область III – r2 < r < r3.
I=I–I ;H=
;H=
 ;B=
;B=
 ;dФ=
;dФ=
 ·l·dr.
·l·dr.
Этот
поток сцеплен с током I
и частью обратного тока, равной I .
.
Поэтому элементарное потокосцепление
d
= dФ·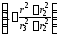 =dФ·
=dФ·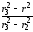 .
.
Внутренняя индуктивность третьей области:
l3
= =
=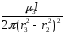
 =
=
=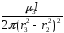 ·[
·[ –
2r
–
2r
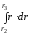 +
+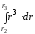 ]=
]=
=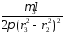 ·[r
·[r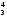 ln
ln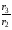 –r
–r (r
(r –r
–r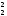 )+
)+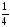 (r
(r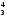 –r
–r )]=
)]=
=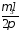 [
[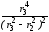 ln
ln –
–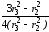 ].
].
Внешняя индуктивность кабеля – lе = l2; внутренняя индуктивность – li = l1 + l3;
вся индуктивность – l = l1 + l2 + l3.
Примерный график зависимости Н(r) представлен на рис. 4.6
Рис.4.6
4.5. Поток вектора Пойтинга в коаксиальном кабеле
Теорема
Умова-Пойтинга позволяет сделать важный
теоретический вывод, что электрическая
энергия от генератора к приемнику
передается не по проводам линии
электропередачи, а электромагнитным
полем, окружающим эти провода, а сами
провода выполняют две другие функции:
1) создают условия для получения электромагнитного поля;
2) являются направляющими для потока электроэнергии.
К кабелю приложено постоянное напряжение U и протекает ток I.
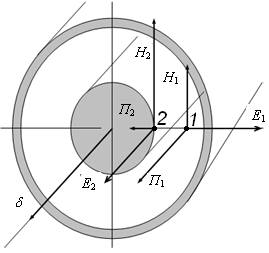
Особенностью режима работы коаксиального кабеля является то, что его электрическое и магнитное поле не выходит за пределы наружной оболочки.
Рассмотрим
режим точки 1, расположенной в диэлектрике
на расстоянии r от
оси кабеля. Линейная плотность
заряда: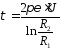 .
.
Радиальная
составляющая напряженности электрического
поля:
 .
.
Вектор
напряженности магнитного поля имеет
только угловую составляющую :
 .
.
Векторы
поля
 и
и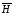 направлены под углом в 90о
друг к другу.
направлены под углом в 90о
друг к другу.
Вектор
Пойтинга: .
.
Поток вектора Пойтинга через поперечное сечение диэлектрика:
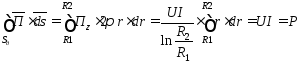 .
.
Вывод: поток вектора Пойтинга через поперечное сечение диэлектрика равен передаваемой мощности Р, т. е. энергия от источника к приемнику передается электромагнитным полем, сосредоточенным в диэлектрике между жилой и оболочкой.
Рассмотрим режим точки 2, расположенной на наружной поверхности жилы.
Плотность
тока в жиле кабеля:
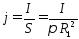 .
.
Составляющая
напряженности электрического поля по
оси z:
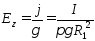 .
.
Напряженность
магнитного поля:
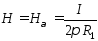 .
.
Векторы
поля
 и
и направлены под углом в 90о
друг к другу.
направлены под углом в 90о
друг к другу.
Радиальная
составляющая вектора Пойтинга:  .
.
Поток вектора Пойтинга через боковую поверхность внутренней жилы:
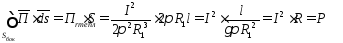 .
.
Вывод:
поток вектора Пойтинга через наружную
поверхность жилы направлен внутрь
провода и равен мощности тепловых потерь
в жиле
 .
.
4.6. Магнитное поле и индуктивность двухпроводной линии
Результирующий
вектор магнитной индукции
 в произвольной точкеn
можно определить по методу наложения
как геометрическую сумму
в произвольной точкеn
можно определить по методу наложения
как геометрическую сумму

составляющих
этого вектора
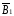 и
и от каждого провода в отдельности:
от каждого провода в отдельности:
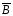 =
=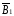 +
+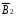 .
Составляющие вектора
.
Составляющие вектора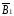 и
и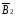 определяются по полученным ранее
формулам, а их направления – по правилу
правоходового винта:
определяются по полученным ранее
формулам, а их направления – по правилу
правоходового винта:
 ,
,
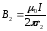 .
.
Индуктивность линии равна L = 2(Lвн+ Lсн). Для определения индуктивности проводника найдем величину тока через сечение радиусом r
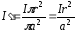
и соответственно, по закону полного тока напряженность магнитного поля
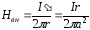
Тогда потокосцепление
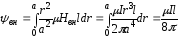
И
внутренняя индуктивность проводника
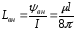 .
.
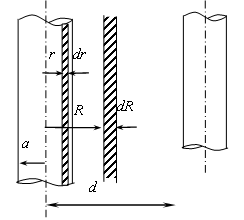
Рис.4.7
Определим потокосцепление между проводниками
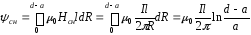
Тогда
Таким образом, индуктивность двухпроводной линии равна
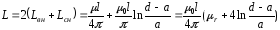 [
Гн / м
]
[
Гн / м
]
Индуктивность трехфазной линии на одну фазу.
В схемах замещения трехфазных линий электропередачи учитывается индуктивность одного провода (фазы), следовательно:
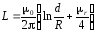 [Гн
/ м] –
индуктивность каждого
провода (фазы) трехфазной транспонированной
ЛЭП на единицу длины, где
[Гн
/ м] –
индуктивность каждого
провода (фазы) трехфазной транспонированной
ЛЭП на единицу длины, где
 – среднегеометрическое значение
межосевых расстояний проводов.
– среднегеометрическое значение
межосевых расстояний проводов.
