4. 2. Векторный потенциал магнитного поля

Как ясно из первого уравнения (4.1), ввести для описания свойств магнитного поля некоторую скалярную функцию подобно тому, как вводится потенциальная функция(см. раздел 4.3), невозможно, так как. Однако из второго уравнения (4.1) следует, что можно ввести некоторую векторную функцию, которая связана с вектором магнитной индукции соотношением:

. (4.6)

Выражение (4.6) вытекает из второго уравнения (4.1) автоматически, поскольку всегда

.

Векторную функцию называютвекторным потенциалом, или векторной потенциальной функцией, магнитного поля.

Вектор связан с векторной потенциальной функциейс точностью до:

, (4.7)

где .

Фактически, это означает, что если к векторному полю (магнитному) прибавить любое поле потенциальное (электрическое), сам векторный потенциал изменится, а магнитное поле– нет. В самом деле

.

Таким образом, векторный потенциал может быть выбран произвольным образом, лишь бы соблюдалось условие (4.6). Это очень удобно, поскольку при расчетах магнитного поля векторуможно присвоить такие свойства, что решение задачи станет значительно проще.

Для векторной функции можно получить уравнения, подобные уравнениям Пуассона-Лапласа. Именно поэтому ее и назваливекторным потенциалом.

Получимуравнение для векторного потенциала . Рассмотрим случай однородной изотропной среды (), когда вектораисвязаны соотношением (3.4). Умножая первое уравнение (7.1) на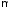, с учетом (3.4) получим:

. (4.8)

Подставляя (7.6) в (7.8), имеем:

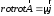. (4.9)

В соответствии с правилами векторной алгебры левая часть (4.9) может быть преобразована следующим образом:

,

тогда уравнение (7.9) примет вид:

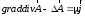. (4.10)

Возьмем такой вектор , чтобы уравнение (4.10) стало как можно более простым, например, пусть

.

В этом случае уравнение (4.10), а значит, и систему (4.1) можно представить как

. (4.11)

Одному векторному уравнению (7.11) соответствуют три скалярных относительно проекций вектора в выбранной системе координат. В декартовой системе получим:

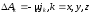(4.12)

Уравнение (7.11) и соответствующая ему система (7.12) определяют вектор в области, где протекают токи (). В областях, свободных от токов, т.е. при, указанные уравнения примут вид:

.

Выражения (4.12) по форме записи совпадают с уравнением Пуассона для скалярной потенциальной функции . Между уравнениями существует математическая аналогия. Следовательно, решение (4.12) совпадает с решением уравнения Пуассона для электростатического поля при аналогичных граничных условиях.

Решение уравнения Пуассона известно и имеет вид

Используя математическую аналогию между величин (,), запишем решение уравнений (4.12):

, (4.13)

где ,,– проекции элемента тока,– расстояние от элемента тока до точки, в которой определяется магнитное поле. Умножая соотношения (4.13) на соответствующие единичные вектора и складывая их почленно, получим решение:

. (4.14)

Решение уравнений (4.11), (4.12) в виде (4.13), (4.14) получается и используется при условии существования токов в ограниченном объеме пространства, что на практике всегда имеет место. При этом, как ясно из (4.13) и (4.14), величина векторного потенциала убывает по мере удаления от области, занятой токами, в бесконечность не медленнее, чем . Так как магнитная индукцияопределяется зависимостью, а операция– есть векторно-пространственная производная, тои соответственно напряженность магнитного поляубывают в бесконечность не медленнее, чем.

Рассмотрим теперь пути нахождения магнитного поля в наиболее важном случае линейного тока. Пусть известна плотность

линейного тока J. Тогда

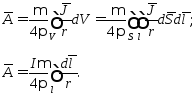
Так как ток , то

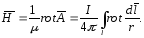(4.15)

Определим подынтегральное выражение.

Пусть , тогда

Соответственно

Так как dl не зависит от положения точки М, в которой находим ротор, то 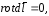а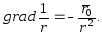

Подставив полученные результаты в уравнение (4.15) получаем

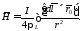
Это интегральная формулировка закона Био и Савара, непосредственно связывающего напряженность магнитного поля с линейным распределением тока.

В дифференциальной форме этот закон имеет вид: