Задача 4.

Определить шаговое напряжение на заданном расстояниих от центра опоры высоковольтной ЛЭП при коротком замыкании одной из фаз линии на опору.

Для упрощения расчетов будем считать, что заземлитель опоры имеет форму полу­шара с радиусом R. Заменим диэлектрик в верхней части пространства проводящей средой γ, а заземлитель дополним зеркальным отображе­нием до полного шара. После таких преоб­разований решение задачи сводится к расчету поля шарового заземлителя:

.

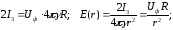
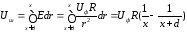где  фазное напряжение ЛЭП, R – радиус заземлителя (фундамента) опоры.

Вопросы для самопроверки

1. Электрический ток является векторной или скалярной величиной?

2. Как определить емкость двухпроводной линии путем моделирования ее полем постоянных токов ?

3. Что такое "шаговое" напряжение, как его рассчитать?

4. Магнитное поле постоянных токов

Возникновение магнитного поля связано с движением электрических зарядов. Движение зарядов с постоянной скоростью порождает стационарное магнитное поле, не зависящее от времени и не связанное с электрическим полем.

4.1. Уравнения магнитного поля в интегральной и дифференциальной формах

Запишем уравнениями Максвелла для магнитного поля постоянного тока, или магнитостатики.

(4.1)

где ₀ = 410^-7  1,257 10^-6 Гн/м  магнитная проницаемость пустоты; _r  относитель­ная магнитная проницаемость.

Из первого уравнения (4.1) следует, что магнитное поле является вихревым (непотенциальным). Согласно второму уравнению (4.1) магнитное поле не имеет источников, линии вектора магнитной индукции непрерывны и замкнупиы.

В интегральной форме система (4.1) может быть представлена следующим образом:

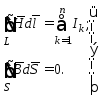(4.2)

Первое уравнение (4.2) также называют законом полного тока. При вычислении алгебраической суммы в правой части уравнения положительными считаются токи, направления которых образуют правовинтовую систему с направлением обхода контура . Второе уравнение (4.2) известно как принцип непрерывности линий магнитной индукции.

Магнитное поле несет в себе энергию, плотность которой определятся уравне­нием

Дж/м³.

Вектор индукции магнитного поля можно записать в виде

, (4.3)

где – вектор намагниченности, или магнитный момент единицы объема.

Вектор характеризуетнамагниченность вещества в магнитном поле подобно тому, как вектор поляризации характеризует поляризацию вещества в электрическом поле.

Способность намагничиваться в магнитном поле характеризуется относительной магнитной проницаемостью . У диамагнитных веществ относительная магнитная проницаемость немного меньше единицы (), у парамагнитных веществ – немного больше единицы (). Магнитная проницаемость ферромагнитных веществ значительно превышает единицу (), к таким веществам относят железо, никель, кобальт и их сплавы, ферриты и др., их магнитная проницаемость достигает. На практике все вещества делят на ферромагнитные () и неферромагнитные ().

Вектор намагниченности пропорционален напряженности магнитного поля:

. (4.4)

Важной характеристикой магнитного поля является магнитный поток сквозь любую поверхность], равный

. (4.5)

Напомним размерности обсуждаемых величин в системе СИ:

, ,.

Между векторами исуществует связь

,

Известный из курса физики закон Био-Савара-Лапласа устанавливает связь между элементар­ным вектором магнитной индукции в произвольной точке про­странства и элементом тока_:

На основе закона Био-Савара-Лапласа выполняется расчет магнитного поля слож­ных систем проводников с токами.

Закон Ампера определяет силу взаимодействия магнитного поля на элеент провод­ника с током

^,

откуда следует, что сила, действующая на проводник , равна

^.

На прямолинейный проводник с током I в равномерном магнитном поле действует сила , направление которой определяется по правилу левой руки.