Введение

В настоящем пособии кратко изложены некоторые разделы третьей части курса ТОЭ – теория электромагнитного поля.

Все электротехнические устройства при полном и детальном их рассмотрении требуют исследования электромагнитных полей, и соответственно, в той или иной мере, необходимо применение теории электромагнитного поля. Вместе с тем представляет большую ценность возможность сведения задач из области электромагнитных явлений к задачам теории электрических и магнитных цепей, которая оперирует только интегральными величинами – электрическим током, напряжением, магнитным потоком и т. д. Весьма важным является установление критериев, в каких случаях допустимо рассмотрение задач как относящихся к теории цепей и когда необходимо их рассматривать как задачи теории поля.

В тех случаях, когда можно не считаться с конечной скоростью распространения волн в диэлектрике, электрическую цепь называют цепью с сосредоточенными параметрами. При периодических процессах критерием допустимости рассмотрения цепи как цепи с сосредоточенными параметрами является малость линейных размеров цепи и ее элементов по сравнению с длиной электромагнитной волны в диэлектрике. Поэтому при промышленной частоте 50 Гц обычные электромагнитные устройства и электрические цепи, за исключением длинных линий, рассматриваются как обладающие сосредоточенными параметрами. Периодические процессы в них часто называют квазистационарными процессами.

Если протяженность электрической цепи столь велика, что промежуток времени, необходимый для прохождения электромагнитной волны вдоль цепи, становится сравнимым с промежутком времени, в течение которого токи или напряжения в отдельных участках цепи успевают заметно измениться, то такую цепь нужно рассматривать как цепь с распределенными параметрами. В простейшем случае, когда цепь имеет большую протяженность лишь в одном направлении, вводят понятие о параметрах, распределенных по длине цепи. Примером таких цепей являются однородные линии.

Однако и этот метод становится уже невозможным в тех случаях, когда длина электромагнитной волны в диэлектрике сравнима с размерами устройств во всех направлениях. В этом случае используется теория электромагнитного поля.

Существует много важных практических случаев, когда анализ электромагнитных явлений может быть произведен только путем детального изучения электромагнитного поля. В качестве примеров можно указать на задачи в технике высоких напряжений, задачи о поверхностных эффектах или об излучении и распространении электромагнитных волн и т.п.

Исследуя электромагнитное поле, необходимо определять все величины, его характеризующие, в каждой точке пространства. Поэтому мы не можем удовлетвориться интегральной формой уравнений и должны представить их в дифференциальной форме.

1. Общие сведения о теории электромагнитного поля

1.1. Понятие поля. Скалярные и векторные поля

В пространстве задано поле некоторой величины, если в каждой его точке определено значение этой величины.

Физическое поле – это любая физическая величина, которая может быть определена для каждой точки пространства. Иначе, это область пространства, с каждой точкой которой связано значение некоторой физической величины. Физическим полем является, например, температура. В каждой точке пространства температура имеет определенное значение, т.е. в пространстве существует температурное поле, которое математически описывается в виде 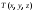. 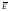Другим примером является электрическое поле, напряженностькоторого также можно определить для каждой точки пространства.

Электромагнитное поле – это физическая реальность.Электромагнитное поле представляет собой вид материи, характеризую­щийся воздей­ствием на заряженные частицы. Как вид материи электромагнит­ное поле обладает массой, энергией, количеством движения, оно может пре­вращаться в вещество и наоборот.

Электромагнитное поле является совокупностью взаимосвязанных и обуславливающих друг друга электрического и магнитного полей.

Следует помнить, что в природе существует единое электромагнитное поле, а отдель­ные его стороны  электрическое или магнитное поле  могут проявляться независимо друг от друга только в частных случаях и при опреде­ленных условиях.

Электромагнитное поле может описываться несколькими математическими полями (скалярным полем - полем потенциала, векторным полем - полем вектора напряженности поля).

Векторным полем называют область пространства, каждой точке которой отнесено значение некоторого вектора. Соответственно называют область пространства, каждой точке которой отнесено значение некоторого скаляра.

Векторные и скалярные поля описывают различные свойства физического поля.