2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией

Наиболее общим методом решения задач электромагнитного поля является метод интегрирования уравнений поля с учетом граничных условий.

Дан цилиндрический конденсатор с внутренней обкладкой радиусом а₁, внешней – радиусом а₂ и границей между слоями диэлектрика радиусом а. Проницаемость слоя в пределах а₁ < r < a равна ε₁, а слоя в предел а < r < a₂ равна ε₂. Длина конденсатора l. Заряд конденсатора q. Рассчитать электрическое поле между обкладками и емкость конденсатора.

Решение

1. Решаем уравнения Лапласа для каждого слоя в отдельности:

.

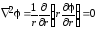Для слоя а₁ ‹ r ‹ a φ₁ = A₁ln r + B₁;

для слоя a ‹ r ‹ a₂ φ₂ = A₂ln r + B₂.

2. Находим напряженность электрического поля как .

Тогда ; .

3. Находим постоянные интегрирования из граничных условий:

при r₁ = a₁ 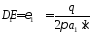, следовательно,.

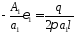Отсюда .

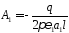При r = a D₁ = D₂, или ₁Е₁= Е₂ε₂; значит, .

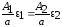Отсюда .

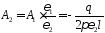4 . Предположим, что φ = 0 при r = a₂ (так как точку нулевого потенциала можно задать произвольно). Тогда .

Из условия непрерывности потенциала во всех точках поля, то есть

,

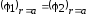получаем .

5. Подставляем значения постоянных интегрирования в выражения для Е и φ:

; ;

; ,

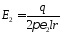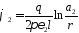где r – координата произвольной точки.

6. Находим напряжение и емкость конденсатора:

.

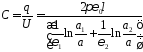7. Находим энергию, накопленную в конденсаторе:

.

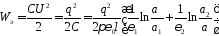2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле

Пусть в однородное электростатическое поле с напряженностью E₀ помещен незаряженный металлический шар радиусом a (рис. 1). Диэлектрик, окружающий шар, имеет относительную диэлектрическую проницаемость ε_r. Требуется рассчитать поле (определить его напряженность 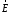, вектор электрической индукции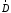и потенциал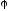) в каждой точке диэлектрика, окружающего шар, а также на поверхности шара.

Рис.2

Решение. Любое однородное поле является бесконечным. При помещении металлического шара в электростатическое поле оно перестает быть однородным. Поле искажается, так как на поверхности шара индуцируется заряд, который, в свою очередь, возбуждает новое поле, накладывающееся на внешнее однородное поле.

Поле внутри шара равно нулю (шар является проводником):

.

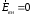В диэлектрике, окружающем его, свободных зарядов нет, поэтому, с математической точки зрения, поле вне шара описывается уравнением Лапласа:

.

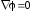Для расчета поля следует выбирать такую систему координат, которая соответствует геометрии рассматриваемой задачи. Так как шар представляет собой сферу, выберем сферическую систему координат, начало которой поместим в центр шара. Координату будем отсчитывать по часовой стрелке от направления вектора(рис.3).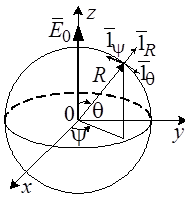

Рис.3

Запишем граничные условия задачи. Вдали от шара поле остается однородным:

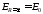. (1)

Поскольку поверхность проводящего шара является эквипотенциальной, ее потенциал не изменяется, т.е.

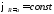. (2)

Исходя из симметрии шара, можно установить, что напряженность поля и потенциал зависят только от двух сферических координат R и θ, т.е. от угла ψ величина потенциала зависеть не будет.

Представив уравнение Лапласа в сферической системе координат

. (3)

Таким образом, расчет поля шара сводится к решению уравнения Лапласа в частных производных (3) с учетом граничных условий (1 и (2). Одним из методов решения таких уравнений является метод разделения переменных, или метод Фурье, согласно которому решение (3) можно найти в виде произведения двух функций, одна из которых зависит только от координаты R, а другая – только от координаты θ, т.е.

. (4)

Подставляя (4) в (3), после соответствующих преобразований получим:

, (5)

где ,.

Из (5) следует, что сумма двух функций, независимых друг от друга, равна нулю. Это возможно только в том случае, когда каждая из них равна постоянной величине:

, .

Соответственно можно записать два уравнения:

, (6)

. (7)

Уравнение (7) есть частный случай широко известного в математике уравнения Лежандра, решение которого имеет вид

. (8)

Подставляя (8) в (7), можно определить значение постоянной :

,

откуда .

С учетом значения постоянной уравнение (6) запишется как

. (9)

Перейдем к новой переменной :

, ,.

Тогда

,

.

Подставляя полученные соотношения в (9), получим:

. (10)

Решение однородного обыкновенного дифференциального уравнения известно:

,

где и– корни характеристического уравнения (10):

,

, ,.

Тогда

.

Подставляя выражение для в (4), найдем окончательное решение уравнения (3):

. (11)

Соотношение (11) определяет потенциал любой точки поля вне шара с точностью до постоянных и.

Напряженность поля вне шара в сферической системе координат складывается из трех составляющих:

, ,

где –проекция на направление единичного радиус-вектора ;– проекцияна направление единичного вектора,–проекция напряженности поля на направление единичного вектора .

С учетом симметрии задачи

,

следовательно, в данном случае

, . (12)

Поскольку электростатическое поле – это потенциальное поле, используя выражение для градиента в сферической системе координат, и симметрию задачи, можно записать:

. (13)

Сравнивая выражения (12) и (13), получим:

(14)

Выражение (11) и система (14) представляют общий вид решения уравнения с точностью до постоянных интегрирования и. Они описывают множество задач электростатики. Решение для поставленной задачи можно найти с помощью граничных.

Поскольку напряженность поля направлена по оси (уголравен нулю), из граничного условия (1) и выражений (14) следует:

,. (15)

Граничное условие примет вид:

.

Это условие должно выполняться при любых значениях угла , что возможно только в случае, когда

,

откуда

. (16)

Искомое решение для проводящего шара:

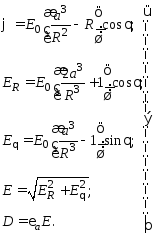
Найдем напряженность электрического поля на поверхности шара:

,

,

. (17)

Из (17) следует, что на полюсах шара (и) напряженность поля будет максимальной, т.е.

.

Таким образом, напряженность электрического поля на полюсах шара в три раза больше напряженности внешнего поля . Этот результат следует учитывать при разработке конструкции проводящих шаровых крыш, куполов. Именно в полюсах шара следует ожидать удара молнии (пробой) во время грозы. Интересно отметить, что максимальное значение напряженности поля не зависит от радиуса шара. Поэтому нетрудно оценить, например, влияние проводящей крупинки, попавшей в изоляцию. Так, капелька воды в баке трансформатора с масляным заполнением вызывает значительное местное увеличение напряженности поля.

Картина силовых и эквипотенциальных линий (картина поля) вокруг проводящего шара представлена на рис. 4.

Рис. 4

Под действием внешнего поля на поверхности шара индуцируется свободный заряд: на верхнем полушарии – положительный заряд, а на нижнем – равный ему по величине отрицательный заряд. В соответствии с (17) рассчитаем плотность индуцированного заряда на поверхности шара:

. (18).

Из (18) следует, что плотность свободного заряда пропорциональна . На рис 5 приведен график изменения плотности индуцированного заряда для верхнего полушария.

Рис. 5	Рис. 6

Определим полный заряд одного полушария:

.

Как видно из рис.6, площадь кольца равна:

,

тогда

.

С учетом (18) получим:

Таким образом, полный заряд шара пропорционален квадрату его радиуса, напряженности внешнего поля и относительной диэлектрической проницаемости окружающей среды.