2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли

Для расчета поля введем две дополнительные оси. Определим потенциал произвольной точки M (рис. 2.14).

Рис. 2.14.

Потенциал произвольной точки от заряженной оси и ее зеркального изображения равен

В данном случае от двух пар линейных зарядов:

.

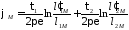Рассчитаем рабочую емкость двухпроводной линии, расположенной над поверхностью земли.

Если провода ли­нии питаются от незазем­ленного источника, то можно принять для первого про­вода , для второго про­вода. Тогда получим:

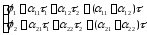
Напряжение между проводами:

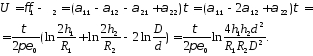
Откуда следует формула рабочей емкости линии с учетом влияния земли:

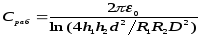[Ф/м].

Для двухпроводной линии рабочую емкость также можно найти как отношение линейного заряда на одном из проводов к напряжению между проводами ().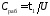

Если линия расположена достаточно высоко над поверхностью земли (h>>d), то D2h и выражение для рабочей емкости превращается в выражение емкости линии без учета влияния земли.

.

2.14.11. Электрическое поле и емкость трехфазной линии электропередачи

Геометрические размеры в поперечном сечении линии электропередачи несравнимо малы по сравнению с длиной электромагнитной волны на частоте 50 Гц (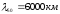). По этой причине волновые процессы в поперечном сече­нии линии могут не учитываться, а по­лученные ранее соотношения для много­проводной линии в статическом режиме с большой степенью точности могут быть применены к расчету поля линий электропередач перемен­ного тока на промышленной частотеf = 50 Гц. Изменяющиеся по синусоидальному закону потенциалы проводов ЛЭП по отношению к параметрам поля можно считать квазистатиче­скими или медленно изменяющимся, и расчет параметров поля для каждого момента времени можно выполнять по полученным ранее уравнениям электростатики.

При синусоидальном законе изменения потенциалов и зарядов проводов формулы Максвелла можно записать в комплексной форме:

.

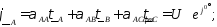
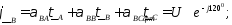
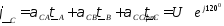Потенциалы проводов ЛЭП равны соответствующим фазным напряже­ниям и опреде­ляются генератором.

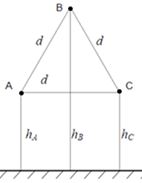
Для трехфазных ЛЭП применяются различные варианты расположения проводов в пространстве. На рис. приведены два из них: по вершинам рав­ностороннего треугольника, в одной плоскости, параллельной поверхности земли. В первом варианте равны расстояния между проводами (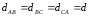), но не равны их высоты над землей ().

Во втором варианте не равны расстояния между проводами (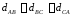), но равны их вы­соты над землей (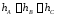). Таким образом, в воз­душных трехфазных ЛЭП не может быть достигнута полная симметрия проводов в про­стран­стве. Потенциальные коэффициенты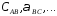, которые определяются через геометриче­ские расстояния, будут несимметрич­ными в формулах первой группы формул Максвелла.

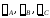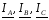Несимметрия потенциальных коэффи­циентов вызо­вет несимметрию зарядов проводов и соответствующую несиммет­рию зарядных токов линиив режиме хо­лостого хода. Полная сим­метрия проводов в пространстве достигается только в кабельных линиях.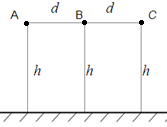

Для устранения несимметрии фаз воздушных линий электропередачи че­рез равные расстояния (обычно через 1/3 длины) производят круговую переста­новку или транспозицию проводов.

При наличии транспозиции усред­ненные значения параметров линии полу­чаются одинаковыми для всех фаз, при этом несимметрия между началом и концом линии устраняется.

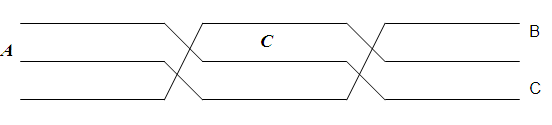
Средние значения потенциалов коэффициентов для транспонированной линии:

.

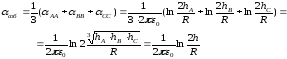
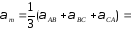
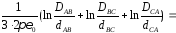
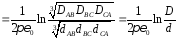где ;;.

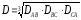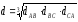Потенциальное уравнение для провода фазы А транспонированной линии получит вид:

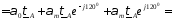
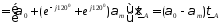
Из полученного выражения следует формула для удельной емкости фазы ЛЭП на землю:

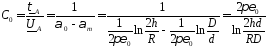[Ф/м].

Если длина линии равна l, то эквивалентная емкость фазы на землю со­ставит С_ф=С₀l, а ток холостого хода линии будет равен I₀ = U_ф/X_C = U_фC.