
- •Основы теории электромагнитного поля
- •Оглавление
- •Введение
- •1. Общие сведения о теории электромагнитного поля
- •1.1. Понятие поля. Скалярные и векторные поля
- •1.2.Основные векторные величины, характеризующие электромагнитное поле
- •1.3. Виды плотности тока
- •1.4.Основные уравнения Максвелла и их физический смысл
- •1.4.1.Закон полного тока
- •1.4.2. Закон электромагнитной индукции
- •1.4.3. Принцип непрерывности магнитной индукции
- •1.4.4. Теорема Гаусса (постулат Максвелла)
- •1.4.5. Система уравнений Максвелла
- •1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга
- •1.6.Частные виды электромагнитных полей
- •Вопросы для самопроверки
- •2.Электростатическое поле
- •2.1. Закон Кулона
- •2.2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •2.3. Электрический потенциал
- •2.4.Картина поля.
- •2.5.Потенциал заданного распределения заряда
- •2.5.1.Потенциал и напряженность электрического поля диполя
- •2.6.Уравнение Пуассона и Лапласа
- •2.7. Поляризация вещества. Вектор поляризации
- •2.8.Проводники в электростатическом поле. Электростатическое экранирование
- •2.9. Граничные условия в электростатическом поле
- •2.9.1.Граничные условия для составляющих векторов поля.
- •2.9.2.Граничные условия для потенциала
- •2.10.Теорема единственности решения
- •2.11.Электрическая емкость
- •2.12. Энергия электростатического поля
- •2.13. Силы, действующие в электростатическом поле
- •2.14.Расчет электростатических полей
- •2.14.1. Поле уединенной равномерно заряженной оси
- •2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей
- •2.14.3.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров (двухпроводной линии)
- •2.14.4.Поле и емкость между несосными, охватывающими друг друга круглыми цилиндрами
- •2.14.5.Поле и емкость системы "цилиндр – плоскость"
- •2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)
- •2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)
- •2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости
- •2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
- •2.14.10.Поле и емкость двухпроводной линии с учетом влияния земли
- •2.14.11. Электрическое поле и емкость трехфазной линии электропередачи
- •2.14.12. Метод интегрирования уравнений Пуассона-Лапласа. Поле и емкость цилиндрического конденсатора с двухслойной изоляцией
- •2. Находим напряженность электрического поля как .
- •2.14.13. Метод разделения переменных. Проводящий шар в однородном электростатическом поле
- •3. Электрическое поле постоянного тока
- •3.1. Электрическое поле в диэлектрике, окружающем проводники с постоянными токами
- •3.2.Электрическое поле постоянного тока в проводящей среде
- •3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
- •3.2.2.Граничные условия на поверхности раздела двух проводящих сред
- •3.2.3. Методы расчета электрических полей постоянного тока
- •3.4.Задачи Задача 1
- •Задача 2. Расчет тока утечки между двумя жилами коаксиального кабеля
- •Задача 3. Заземлитель в виде шара
- •Задача 4.
- •Вопросы для самопроверки
- •4. Магнитное поле постоянных токов
- •4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •4. 2. Векторный потенциал магнитного поля
- •4.3. Выражение магнитного потока и энергии через векторный потенциал
- •4.4.Граничные условия в магнитном поле
- •4.3.1. Граничные условия для векторного потенциала магнитного поля
- •4.3. Скалярный потенциал магнитного поля
- •4.3. Магнитное поле цилиндрического проводника с током
- •4.4.Магнитное поле коаксиального кабеля
- •4.5. Поток вектора Пойтинга в коаксиальном кабеле
- •4.6. Магнитное поле и индуктивность двухпроводной линии
- •4.7. Взаимная индуктивность двух параллельных линий
- •4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током
- •4.9. Графический метод построения картины поля
- •4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Методзеркальных изображений
- •4.11.Магнитное экранирование
- •Вопросы для самопроверки
- •5. Переменное электромагнитное поле
- •5.1. Уравнения Максвелла в комплексной форме
- •5.2 Плоская гармоническая волна в диэлектрике
- •5.3. Плоская гармоническая волна в проводящей среде
- •5.4. Магнитный поверхностный эффект в плоском листе
- •5.5.Электрический поверхностный эффект
- •5.6.Эффект близости
- •5.7. Поверхностный эффект в круглом проводе
- •5.8. Экранирование в переменном магнитном поле
- •5.9.Высокочастотный нагрев металлических деталей и несовершенных диэлектриков
- •5.10. Излучение электромагнитной энергии
- •Вопросы для самопроверки
- •Приложение Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат
- •Литература
2.14.9. Потенциальные коэффициенты, коэффициенты электростатической индукции (емкостные коэффициенты) и частичные емкости системы проводников.
Как пример практического применения метода зеркальных изображений рассмотрим расчет потенциалов и зарядов в системе проводящих тел. Задачи такого типа возникают, в частности, при исследовании процессов в линиях электропередач.
Два
длинных провода
расположенны параллельно проводящей
плоскости (над землею). Радиусы проводов
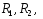 высоты подвесок
высоты подвесок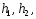 межосевое расстояние
межосевое расстояние при этомh>>R,
d>>R.
Известны
при этомh>>R,
d>>R.
Известны
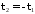 .
.
На
основании второго следствия из теоремы
единственности заменим проводящую
среду (землю) диэлектриком с
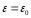 ,
а поверхностные заряды земли – системой
зеркальных зарядов проводов с
противоположными знаками. Смещением
электрических осей пренебрегаем,
так как по условиюh>>R.
,
а поверхностные заряды земли – системой
зеркальных зарядов проводов с
противоположными знаками. Смещением
электрических осей пренебрегаем,
так как по условиюh>>R.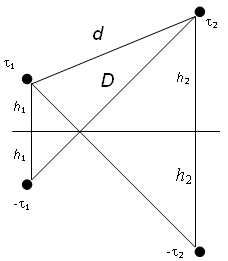
Потенциальные коэффициенты.
Потенциалы проводов можно определить через линейные плотности зарядов:

или
 (2.12)
(2.12)
Здесь обозначены:
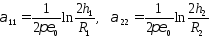 собственные
потенциальные коэффициенты;
собственные
потенциальные коэффициенты;
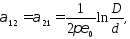 взаимные
потенциальные коэффициенты.
взаимные
потенциальные коэффициенты.
Систему уравнений (2.12) принято называть первой группой формул Максвелла. Первая группа формул Максвелла позволяет определить потенциалы проводов через их заряды.
Коэффициент
 численно равен потенциалуn-го
провода, если на нем находится единичный
заряд (
численно равен потенциалуn-го
провода, если на нем находится единичный
заряд ( ),
а на остальных проводах заряды отсутствуют.
Коэффициент
),
а на остальных проводах заряды отсутствуют.
Коэффициент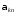 численно равен потенциалу
численно равен потенциалу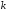 -го
провода, если заряд
-го
провода, если заряд -го
провода равен единице, а остальных
проводов – нулю.
-го
провода равен единице, а остальных
проводов – нулю.
Емкостные коэффициенты (коэффициенты элетростатической индукции).
Если
заданы потенциалы проводов
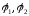 ,
то их заряды
,
то их заряды могут быть определены из совместного
решения системы потенциальных уравнений
(первой группы формул Максвелла). Тогда
получим вторую группу формул Максвелла
могут быть определены из совместного
решения системы потенциальных уравнений
(первой группы формул Максвелла). Тогда
получим вторую группу формул Максвелла
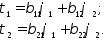 (2.13)
(2.13)
Здесь приняты обозначения:
 -
собственные емкостные коэффициенты
(коэффициенты элетростатической
индукции) всегда положительны,
-
собственные емкостные коэффициенты
(коэффициенты элетростатической
индукции) всегда положительны,
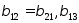 - взаимные
емкостные коэффициенты, всегда
отрицательны.
- взаимные
емкостные коэффициенты, всегда
отрицательны.
Частичные ёмкости.
Систему уравнений (2.13) можно записать в другой форме, выражая заряды на проводящих телах через разности потенциалов (напряжения) между некоторым телом и всеми остальными, в т.ч. и землей.
Запишем систему уравнений (2.13) в виде
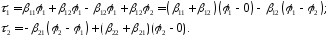
Введем
обозначения: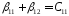 ;
;
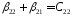 ;
;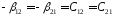 .
.
С учетом введенных обозначений выражение (2.13) перепишется в форме:
 (2.14)
(2.14)
Здесь
обозначены: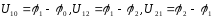
напряжения между соответствующими
элементами схемы;
напряжения между соответствующими
элементами схемы;
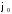 =0
.
=0
.
Итак, чстичные емкости определяются через коэффициенты элетростатической индукции.
Частичные
емкости являются важными характеристиками
системы заряженных проводящих тел. С
их помощью такая система может быть
представлена в виде определенной
комбинации емкостей. 
На рис. 2.13 в виде схемы соединений частичных емкостей представлена система двух проводящих тел.
Частичные емкости используют при расчетах не только электростатических полей, но и быстропротекающих процессов в электрических цепях, а также при расчетах таких процессов в электрических цепях, в основу которых положено использование частичных емкостей, например, при емкостном отборе мощности от высоковольтной линии электропередачи. При расчете быстропротекающих процессов учитывают, в частности, емкости между электродами полупроводниковых приборов (тиристоров, транзисторов).
