2.14.6.Поле цилиндрического конденсатора (коаксиального кабеля)

Дан цилиндрический конденсатор с радиусом внутреннего проводника (жилы)r₁ и внутренним радиусом оболочки r₂. Известно напряжение U между обкладками. Выяснить зависимость Е и φ(r) и определить такое значение радиуса жилы r₁, при котором напряженность электрического поля Е на поверхности жилы будет минимальной.

Решение.

Рассматриваем жилу как заряженную ось, тогда по теореме Гаусса: ;

.

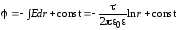Наибольшее значение Е будет на поверхности жилы:

.

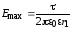Определяем потенциалы жилы и облочки:

; .

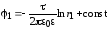По известному значению U = φ1 – φ2 определяем заряд τ:

; .

Тогда .

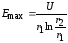Для определения минимального значения E_max берем производную от знаменателя по r₁ и приравниваем нулю:

; ;.

2.14.7.Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи границы раздела двух диэлектриков (задача Сирла)

Рассмотрим поле оси, расположенной на расстоянии h от границы раздела двух диэлектриков с диэлектрическими проницаемостями ₁ и ₂.

Вследствие разной поляризации диэлектриков на границе раздела выявятся связанные заряды, влияющие на поле в обеих средах. Поле создается свободным зарядом 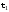, а также поверхностным связанным зарядом на границе раздела двух сред. Распределение связанных зарядов неизвестно.

Возникает довольно сложная задача: чтобы определить поле, необходимо знать распределение зарядов по поверхности, а его можно найти по граничному условию, зная напряженность поля. Этот замкнутый круг легко разорвать, применив метод зеркальных изображений.

Математическим обоснованием метода изображений является следствие теорема единственности решения.

Электростатическое поле по одну сторону некоторой поверхности S не изме­нится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположение свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.

Согласно методу вместо расчета поля в неоднородной среде решают две эквивалентные задачи о поле в однородной среде.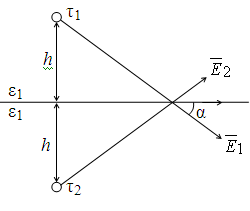

Расчет поля в верхней части пронстранства ведется от двух зарядов: реального ₁ и фиктивного ₂, расположенных симметрично относительно границы раздела;

причем среда всюду имеет диэлектрическую проницаемость ₁.

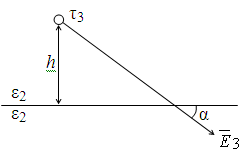
Расчет поля в нижней части пронстранства ведется от заряда ₃, расположенного в той же точке, что и ₁. Среда при этом всюду имеет проницаемость ₂.

Величины и знаки зарядов иопределяются из требования неизменности граничных условий в исходной и эквивалентных задачах.

Граничные условия реальной задачи:

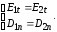
В расчетной модели:

или .

Осюда получаем

; ,

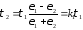Где k₁ и k₂ называют коэффициентами неполного отражения.

Если относительную диэлектрическую проницаемость устремить к бесконечности (вторая среда – проводник), то получим все соотношения для расчета поля заряженной оси, расположенной над проводящей плоскостью. При этом с учето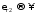мимеем

.

В нижней полуплоскости поле не исследуется, поскольку оно известно и равно нулю.

2.14.8.Поле заряженной оси, расположенной вблизи проводящей плоскости

Положительно заряженная ось (на практике – тонкий длинный провод) с зарядом на единицу длины расположена в среде с относительной диэлектрической проницаемостью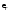параллельно проводящей плоскости (металлическая стенка, земля) на расстоянииот нее.

В результате электростатической индукции на поверхности проводящей плоскости появляются свободные заряды. Поле в диэлектрике создается не только заряженной осью, но и выступившими на поверхность зарядами.

Рассматриваемая задача эквивалентна задаче о поле двух заряженных осей, расположенных на равных расстояниях от плоскости нулевого потенциала в безграничной среде с относительной диэлектрической проницаемостью .

Согласно теореме единственности решения электрическое поле над проводящей плоскостью (рис. 2.10) эквивалентно электрическому полю в верхней полуплоскости на рис.2.11.Действительно, уравнения, описывающие поля в этих задачах, одинаковы (уравнение Лапласа); граничные условия также одинаковы.

Рассчитаем индуцированный заряд на границе раздела сред. В любой точке, принадлежащей поверхности раздела (рис. 2.11), напряженность поля согласно (5.6) равна

.

Как видно из рис. 2.11, вектор напряженности поля противоположен нормали 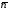. нормальная проекция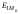определится как

,

где ;– координата точки на проводящей поверхности относительно положения заряженной оси.

Окончательно получаем

,

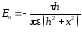откуда поверхностная плотность индуцированного заряда имеет вид

.

Индуцированный заряд имеет знак, противоположный знаку линейного заряда. Распределение заряда представлено на рис. 2.12 кривой (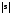– модуль индуцированного заряда).

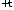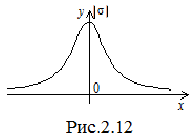
Поскольку заряд отражает в эквивалентной задаче все заряды, индуцированные на границе раздела, силу притяжения положительно заряженной оси к проводящей плоскости определим как силу взаимодействия двух заряженных осейи: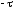

, ,

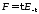где – напряженность электрического поля, созданного осью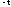в точке расположения заряженной оси, согласно (5.2)

.

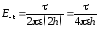Таким образом, заряженная ось испытывает силу притяжения к плоскости, равную по величине

.