3.2 Локальная теорема Муавра-Лапласа

Теорема.Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна

,

(3.3)

где

.

(3.4)

Эта приближенная формула тем точнее, чем больше nи чем ближе к 0,5 значенияpиq. Вычисление по этой формуле дает незначительную погрешность при выполнении условияnpq≥ 20, хотя допустимым можно считать выполнение условияnpq> 10.

Для упрощения расчетов, связанных с применением локальной формулы Муавра-Лапласа, составлена таблица значений функции φ(x) (см. Приложение 1). Пользуясь этой таблицей, необходимо иметь в виду следующие свойства функцииφ(x):

1. Функция φ(x) является четной, т.е.φ(–x) =φ(x).

2. Функция φ(x) – монотонно убывающая при положительных значенияхx, причем приx→ ∞φ(x) → 0 (практически можно считать, что уже приx≥ 5φ(x)≈0).

Пример 3.3.По результатам многолетних наблюдений известно, что экзамен по теории вероятностей с первого раза успешно сдают в среднем 80% студентов. Найти вероятность того, что из 400 студентов 2-го курса 300 успешно сдадут экзамен с первого раза.

Решение.По условиюn= 400,m= 300,p= 0,8,q= 0,2. Так какnpq=400·0,8·0,2 = 64 > 20, то условие применимости локальной формулы Муавра-Лапласа (npq≥ 20) выполняется.

Вначале определяем == – 2,5.

По таблице значений функции φ(x) находимφ(– 2,5) = 0,0175.

Находим вероятность того, что ровно 300 студентов из 400 успешно сдадут экзамен с первого раза:

≈0,0022.

Относительно малое значение вероятности не должно вызывать сомнений, так как кроме события «ровно 300 студентов успешно сдадут экзамен с первого раза» возможно еще 400 событий: «0 из 400», «1 из 400» и т.д. Каждое из этих событий обладает своей вероятностью, а все вместе они образуют полную группу событий и, следовательно, сумма их вероятностей равна единице. ◄

Пусть в условиях этого примера необходимо найти вероятность того, что от 300 до 360 студентов (включительно) успешно сдадут экзамен с первого раза. В этом случае по теореме сложения вероятность искомого события

P₄₀₀(300 ≤ m ≤ 360) = P₄₀₀(300) + P₄₀₀(301) + … +P₄₀₀(360).

В принципе каждое слагаемое можно вычислить по локальной формуле Муавра-Лапласа, но большое число слагаемых делает расчет весьма громоздким. В таких случаях используется интегральная теорема Лапласа.

3.3. Интегральная теорема Лапласа

Теорема.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе испытаний n приближенно равна

,

(3.5)

где

–

(3.6)

функция(илиинтеграл вероятностей)Лапласа;

;.

(3.7)

Интегральная формула Лапласа, также как и локальная формула Муавра-Лапласа, тем точнее, чем больше nи чем ближе к 0,5 значенияpиq. Вычисление по этой формуле дает незначительную погрешность при выполнении условияnpq≥ 20, хотя допустимым можно считать выполнение условияnpq> 10.

Функция Ф(x) табулирована (см. Приложение 2). Для применения этой таблицы нужно знать свойства функции Ф(x):

1. Функция Ф(x) – нечетная, т.е. Ф(–x) = – Ф(x).

2. Функция Ф(x) – монотонно возрастающая, причем приx→ +∞ Ф(x) → 0,5 (практически можно считать, что уже приx≥ 5 Ф(x) ≈ 0,5).

Пример 3.4.По условиям примера 3.3 вычислить вероятность того, что от 300 до 360 (включительно) студентов успешно сдадут экзамен с первого раза.

Решение.Применяем интегральную теорему Лапласа (npq≥ 20). Вычисляем:

= –2,5; = 5,0;

P₄₀₀(300 ≤m≤ 360) = Ф(5,0) – Ф(–2,5).

Учитывая свойства функции Ф(x) и пользуясь таблицей ее значений, находим: Ф(5,0) = 0,5; Ф(–2,5) = – Ф(2,5) = – 0,4938.

Получаем P₄₀₀(300 ≤m≤ 360) = 0,5 – (– 0,4938) = 0,9938.◄

Запишем следствия интегральной теоремы Лапласа.

Следствие 1.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что число m наступления события А отличается от произведения np не более, чем на величину ε > 0 (по абсолютной величине) равна

.

(3.8)

Пример 3.5.По условиям примера 3.3 найти вероятность того, что от 280 до 360 студентов успешно сдадут экзамен по теории вероятностей с первого раза.

Решение.Вычислить вероятностьР₄₀₀(280 ≤m≤ 360) можно аналогично предыдущему примеру по основной интегральной формуле Лапласа. Но проще это сделать, если заметить, что границы интервала 280 и 360 симметричны относительно величиныnp=320. Тогда на основании следствия 1 получаем

= =≈

≈ = 2Ф(5,0) ≈ 2·0,5 ≈ 1,

т.е. практически достоверно, что от 280 до 360 студентов успешно сдадут экзамен с первого раза. ◄

Следствие 2.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что частость m/n события А заключена в пределах от α до β (включительно) равна

,

(3.9)

где

, .

(3.10)

Пример 3.6.По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет заключена в пределах от 0,9 до 0,95.

Решение.Вероятность того, что новорожденный доживет до 50 лет равнар= 0,87. Так какn= 1000 велико (т.е. условиеnpq= 1000·0,87·0,13 = 113,1 ≥ 20 выполнено), то используем следствие 2 интегральной теоремы Лапласа. Находим:

= 2,82, = 7,52.

= 0,5 – 0,4976 = 0,0024. ◄

Следствие 3.Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе n независимых испытаний вероятность того, что частость m/n события А отличается от его вероятности р не более, чем на величину Δ > 0(по абсолютной величине) равна

.

(3.11)

Пример 3.7.По условиям предыдущей задачи найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине).

Решение.Используя следствие 3 интегральной теоремы Лапласа, находим:

= 2Ф(3,76) = 2·0,4999 = 0,9998.

Так как неравенство равносильно неравенству, полученный результат означает, что практически достоверно, что от 83 до 91% новорожденных из 1000 доживут до 50 лет.◄

Ранее мы установили, что для независимых испытаний вероятность числа mпоявлений событияАвnиспытания находится по формуле Бернулли. Если жеnвелико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р≤ 0,1). В этом случае (nвелико,рмало) применяют теорему Пуассона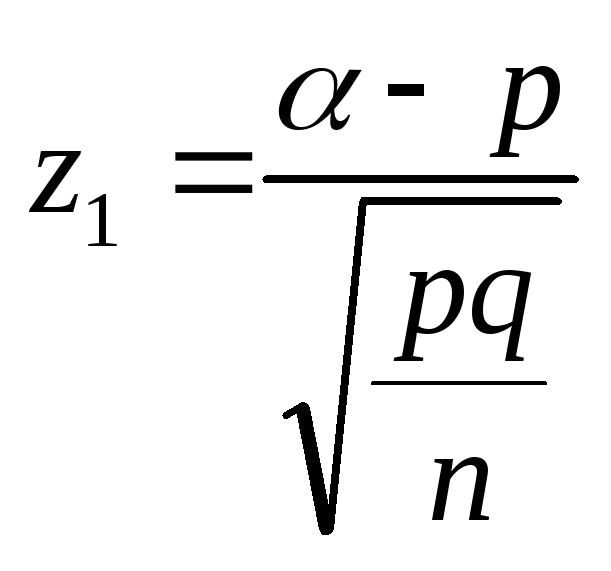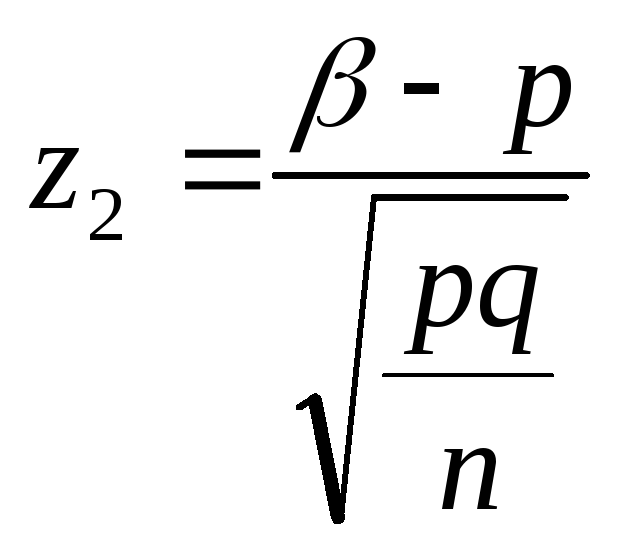