8.3. Функция распределения многомерной случайной величины

При изучении одномерных случайных величин уже говорилось, что самой универсальной характеристикой случайной величины является функция распределения. Она существует для всех случайных величин: как дискретных, так и непрерывных. Точно также функция распределения полностью характеризует и многомерную случайную величину.

Определение. Функцией распределения n-мерной случайной величины (Х₁, Х₂, …, Х_n) называется функция F(x₁, x₂, …, x_n), выражающая вероятность совместного выполнения n неравенств Х₁ < х₁, Х₂ < х₂, …, Х_n < x_n, т.е.

F(x1, x2, …, xn) = Р(Х1 < х1, Х2 < х2, …, Хn < xn).

(8.1)

В случае двумерной случайной величины XY функция распределения определяется неравенством

F(x, y) = P(X < x, Y < y).

(8.2)

Г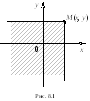еометрически функция распределенияF(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна слева по каждому аргументу.

В случае двумерной дискретной случайной величины ее функция распределения определяется по формуле:

,

(8.3)

где суммирование вероятностей распространяется на все j, для которых x_j < x, и все i, для которых y_i < y.

Отметим свойства функции распределения двумерной случайной величины.

1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей, т.е.

0 ≤ F(x, y) ≤ 1.

(8.4)

2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е.

при x2 > x1 F(x2, y) ≥ F(x1, y), при y2 > y1 F(x, y2) ≥ F(x, y1).

(8.5)

3. Если хотя бы один из аргументов обращается в – ∞, то функция распределения равна нулю, т.е.

F(x, – ∞) = F(– ∞, y) = F(– ∞, – ∞) = 0.

(8.6)

4. Если один из аргументов обращается в + ∞, то функция распределения становится равной функции распределения случайной величины, соответствующей другому аргументу, т.е.

F(x, + ∞) = F1(x), F(+ ∞, y) = F2(y),

(8.7)

где F₁(x) и F₂(y) – функции распределения случайных величин X и Y, т.е.

F₁(x) = P(X < x), F₂(y) = P(Y < y).

5. Если оба аргумента равны + ∞, то функция распределения равна единице:

F(+ ∞; + ∞) = 1.

(8.8)

Геометрически функция распределения есть некотораяповерхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y).

Зная функцию распределения F(x, y) можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 8.2). Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной B(x₂, y₂) минус вероятность попадания в квадранты с вершинами в точках A(x₁, y₂) и C(x₂, y₁) плюс вероятность попадания в квадрант с вершиной в точке D(x₁, y₁) (так как эта вероятность вычиталась дважды), т.е.

P[(x1 ≤ X < x2)(y1 ≤ Y <y2)] = F(x2, y2) – F(x1, y2) – F(x2, y1) + F(x1, y1).

(8.9)