
- •Министерство транспорта российской федерации
- •Введение
- •1. Основные понятия теории вероятностей
- •1.1. События. Классификация событий
- •1.2. Классическое и статистическое определение вероятности
- •1.3. Элементы комбинаторики
- •2. Алгебра событий
- •2.1. Действия над событиями
- •2.2. Теорема сложения вероятностей несовместных событий
- •2.3. Зависимые и независимые события
- •2.4. Теорема умножения вероятностей независимых событий
- •2.5. Вероятность появления хотя бы одного события
- •2.6. Условная вероятность
- •2.7. Теорема умножения вероятностей зависимых событий
- •2.8. Теорема сложения вероятностей совместных событий
- •2.9. Формула полной вероятности
- •2.10. Вероятность гипотез. Формула Байеса
- •3. Повторные независимые испытания
- •3.1. Формула Бернулли
- •3.2 Локальная теорема Муавра-Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Формула Пуассона
- •4. Случайные величины
- •4.1. Понятие случайной величины
- •4.2. Закон распределения случайной величины
- •4.3. Функция распределения случайной величины
- •4.4. Плотность вероятности
- •5. Числовые характеристики случайных величин
- •5.1. Математическое ожидание случайной величины
- •5.2. Дисперсия случайной величины
- •5.3. Среднее квадратическое отклонение случайной величины
- •5.4. Мода и медиана. Квантили
- •Решение. Находим функцию распределения
- •5.5. Моменты случайных величин. Асимметрия и эксцесс
- •5.6. Числовые характеристики независимых испытаний
- •5.7. Одинаково распределенные взаимно независимые случайные величины
- •6. Основные законы распределения
- •6.1. Биноминальный закон распределения
- •6.2. Закон распределения Пуассона
- •6.3. Равномерный закон распределения
- •6.4. Показательный (экспоненциальный) закон распределения
- •6.5 Функция надежности
- •6.6. Нормальный закон распределения
- •7. Предельные теоремы теории вероятностей
- •7.1. Закон больших чисел
- •7.1.1. Неравенство Чебышёва
- •7.1.2. Теорема Чебышёва
- •7.1.3. Теорема Бернулли
- •7.1.4. Теорема Пуассона
- •7.1.5. Теорема Маркова
- •7.2.Центральная предельная теорема
- •7.2.1. Теорема Ляпунова
- •7.2.2. Теорема Берри-Эссена
- •8. Многомерные случайные величины
- •8.1. Понятие многомерной случайной величины
- •8.2. Закон распределения вероятностей двумерной дискретной случайной величины
- •8.3. Функция распределения многомерной случайной величины
- •8.4. Плотность вероятности двумерной случайной величины
- •8.5. Условные законы распределения двумерной случайной величины
- •8.6. Зависимые и независимые случайные величины
- •8.7. Числовые характеристики двумерной случайной величины.
- •Библиографический список
- •Оглавление
- •Лаврусь Ольга Евгеньевна Конспект лекций по теории вероятностей
- •443022, Г. Самара, Заводское шоссе, 18
8.4. Плотность вероятности двумерной случайной величины
Для непрерывной двумерной случайной величины, так же как и для одномерной, существует понятие плотности вероятности.
Определение. Плотностью вероятности (или совместной плотностью) непрерывной двумерной случайной величины XY называется вторая смешанная частная производная ее функции распределения, т.е.
|
|
(8.10) |
Г еометрически
плотность вероятности двумерной
случайной величиныXY
представляет собой поверхность
распределения в пространстве Oxyz.
еометрически
плотность вероятности двумерной
случайной величиныXY
представляет собой поверхность
распределения в пространстве Oxyz.
Отметим свойства плотности вероятности двумерной случайной величины.
1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.
f(x, y) ≥ 0.
2. Вероятность попадания непрерывной случайной величины XY в область D равна
|
|
(8.11) |
3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле:
|
|
(8.12) |
4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:
|
|
(8.13) |
Зная плотность вероятности двумерной случайной величины (X, Y) можно найти функции распределения и плотность вероятностей ее одномерных составляющих X и Y.
Так как в соответствии с (8.7) F(x, + ∞) = F1(x) и F(+ ∞, y) = F2(y), то взяв в формуле (8.12) соответственно x = + ∞ и y = + ∞, получим функции распределения одномерных случайных величин X и Y:
|
|
(8.14) |
Дифференцируя функции распределения F1(x) и F2(y) соответственно по аргументам x и y, получим плотности вероятности одномерных случайных величин X и Y:
|
|
(8.15) |
т.е. несобственный интеграл в бесконечных пределах от совместной плотности двумерной случайной величины по аргументу x дает плотность вероятности f2(y), а по аргументу y – плотность вероятности f1(x).
8.5. Условные законы распределения двумерной случайной величины
Итак, мы выяснили, как по известному закону распределения системы двух случайных величин определить законы распределения одномерных величин, входящих в систему.
Естественно возникает вопрос: нельзя ли по законам распределения одномерных величин, входящих в систему, найти закон распределения системы в целом? Оказывается, в общем случае этого сделать нельзя. Для того, чтобы полностью описать систему случайных величин, недостаточно знать распределение каждой из ее составляющих. Нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.
Определение. Условным законом распределения одной из одномерных составляющих двумерной случайной величины XY называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в определенный интервал).
Для дискретных случайных величин условные вероятности находятся по формулам:
|
|
(8.16) |
|
|
(8.17) |
В случае непрерывных случайных величин необходимо определить плотность вероятности условных распределений. Заменяя в формулах для дискретных величин вероятности событий «элементами вероятностей», получим:
|
|
(8.18) |
т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равно отношению ее совместной плотности к плотности вероятности другой составляющей.
Пример 8.2.По данным примера8.1найти условный закон распределения составляющейХпри условии, сто составляющаяYприняла значениеy1=1.
Решение.Искомый закон определяется следующей совокупностью условных вероятностей:
p(x1|y1),p(x2|y1),p(x3|y1).
Воспользовавшись формулой (8.16) и учитывая, чтоp(y1) = 0,6 (пример8.1), получаем:
p(x1
| y1)
=
 ;p(x2
| y1)
=
;p(x2
| y1)
=
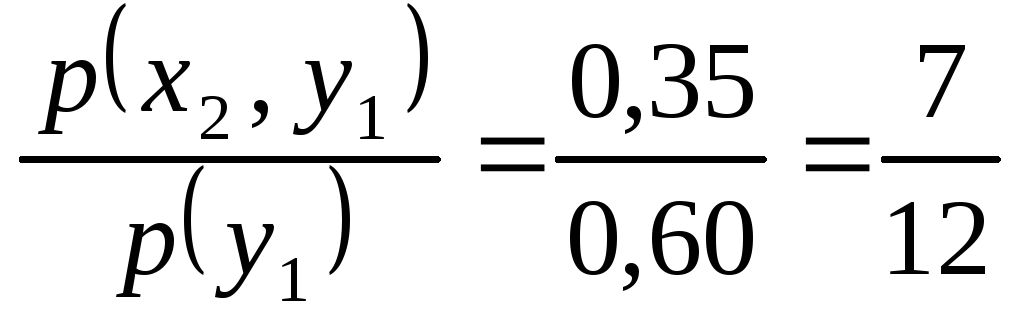 ;
;
p(x3
| y1)
=
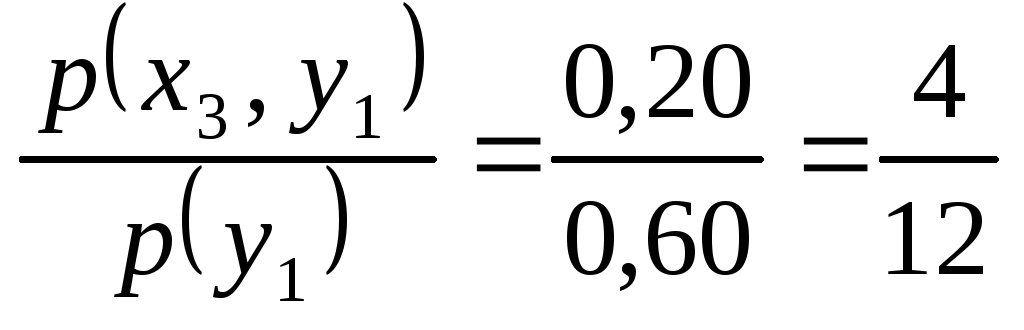 .◄
.◄
Важной характеристикой условного распределения вероятностей является условное математическое ожидание.
Условным математическим ожиданиемдискретной случайной величиныYприХ=х(х– определенное возможное значениеХ) называют произведение возможных значенийYна их условные вероятности:
|
|
(8.19) |
Для непрерывных величин
|
|
(8.20) |
Аналогично определяется условное математическое ожидание случайной величины Х.
Пример 8.3. По данным примера8.1найти условное математическое ожидание составляющейYпри условии, что составляющаяХпримет значениех1= 2.
Решение.Найдемр(х1), для чего сложим вероятности, помещенные в первом столбце табл. 8.2
р(х1) = 0,05 + 0,15 = 0,2.
Найдем условное распределение вероятностей величины Yпри приХ=х1=3:
p(y1
| x1)
=
 ;p(y2
| x1)
=
;p(y2
| x1)
=
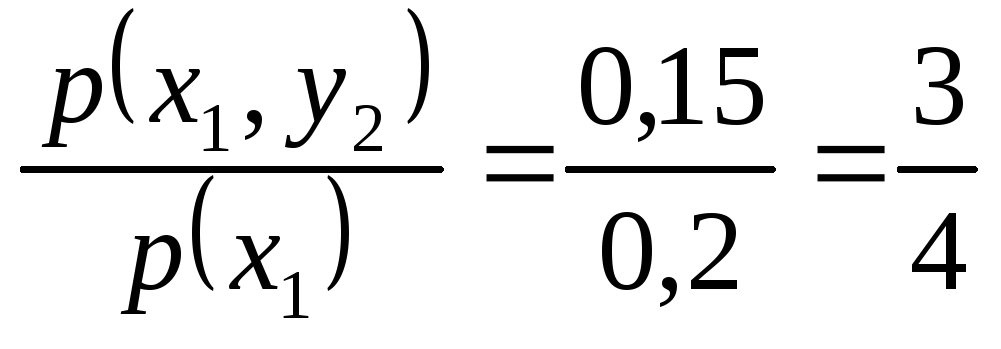 .
.
Найдем условное математическое ожидание по формуле (8.19):
M(Y|X=x1)
=
![]() =y1·p(y1|x1) +y2·p(y2|x1) =
=y1·p(y1|x1) +y2·p(y2|x1) =
![]() =
2,5. ◄
=
2,5. ◄
Условное математическое ожидание случайной величины YприХ=х, т.е.Mx(Y), есть функция отх, называемаяфункцией регрессииили просторегрессиейYпо Х. АналогичноMy(X) называетсяфункцией регрессииилирегрессией X по Y. Графики этих функций называются соответственнолиниями регрессии(иликривыми регрессии)Y по ХиХ по Y.

 или
или
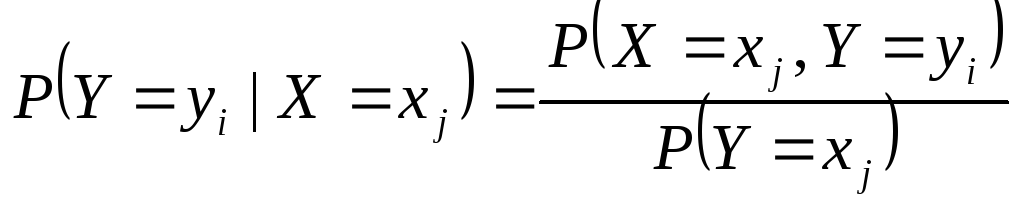 или
или