Управление качеством в приборостроении

Раздел I. Методы и средства управления качеством

____________________________________________________________________

Analysis of Variance for prochnost - Type III Sums of Squares

--------------------------------------------------------------------------------

Source Sum of Squares Df Mean Square F-Ratio P-Value

--------------------------------------------------------------------------------

--------------------------------------------------------------------------------

--------------------------------------------------------------------------------

All F-ratios are based on the residual mean square error.

The StatAdvisor

---------------

The ANOVA table decomposes the variability of prochnost into contributions due to various factors. Since Type III sums of squares (the default) have been chosen, the contribution of each factor is measured having removed the effects of all other factors. The P-values test the statistical significance of each of the factors. Since 6 P-values are less than 0,05, these factors have a statistically significant effect on prochnost at the 95,0% confidence level.

3.4.Использование методов корреляционного анализа

взадачах исследования качества техпроцессов

3.4.1.Корреляция параметров

Как было отмечено ранее в технике, да и в жизни вообще, кроме жестких, т.е. функциональных связей между параметрами существует так называемый вероятностный или стохастический характер связи, при котором каждому значению одного из параметров, может соответствовать одно или несколько значений другого параметра.

Для количественной оценки силы вероятностной связи между параметрами обычно используют математический аппарат корреляционного анализа.

Поэтому вероятностную связь между параметрами часто называют корреляционной связью.

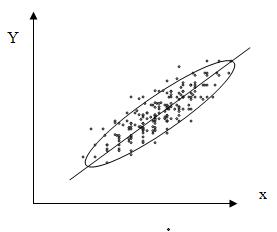
Начальное суждение о силе корреляционной связи можно получить по виду так называемого корреляционного поля параметров. Корреляционное поле параметров представляет собой совокупность точек, нанесенных на прямоугольную систему координат, причем каждая точка соответствует паре рассматриваемых параметров. В технике с каждой точкой корреляционного поля связан экземпляр объекта или реализация процесса.

101

Глава 3. Методы оценки точности

________________________________________________________________________________

Если точки корреляционного поля группируются вблизи прямой линии, мысленно проведенной в этом поле, то между параметрами имеет место тесная корреляционная связь, рис. 3.1.

Рис. 3.1. К пояснению корреляционной связи.

Для количественной оценки тесноты или силы связи между параметрами

где x, z – рассматриваемые параметры;

xi , zi – i -е значение параметра х и соответствующее ему значение параметра z;

mx , mz – математические ожидания параметров х и z;

x , 2 – средние квадратичные отклонения параметров х и z;

n – число наблюдений пар параметров х и z.

Коэффициент корреляции, подсчитываемый по формуле (3.6), лежит в пределах от –1 до +1. Он характеризует близость корреляционной связи между параметрами к их линейной функциональной зависимости. Между параметрами имеет место линейная функциональная связь, если r = ±1.

Различают отрицательную и положительную корреляцию между параметрами. Для отрицательной корреляции r < 0, для положительной r > 0.

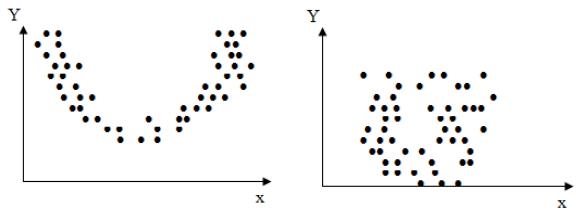
Если r = 0, то мы имеем дело практически с независимыми параметрами. Вид корреляционного поля в этом случае близок к показанному на рис. 3.3.

Известны случаи, когда коэффициент корреляции, подсчитываемый по выражению (3.6), оказывается близким к нулю, но между параметрами существует тесная связь (рис. 3.2).

Дело здесь в том, что коэффициент, подсчитываемый по выражению (3.6), выявляет лишь линейную составляющую вероятностной связи между параметрами. По этой причине его часто называют коэффициентом линейной корреляции (существует еще и криволинейная корреляция).

102

Раздел I. Методы и средства управления качеством

____________________________________________________________________

Коэффициент, определяемый по выражению (3.6), называют также коэффициентом парной корреляции, имея ввиду, что рассматривается корреляция между парой параметров. Существует также такое понятие, как множественная корреляция.

Использования метода можно проиллюстрировать следующим примером.

Пример 3.3 [ 23 ]. В таблице представлены данные параметра интегральных схем до и после обработки (технологической операции). Необходимо оценить влияние технологической операции на величину параметр.

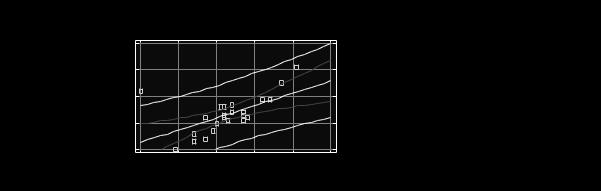
Как следует из распечатки результатов, коэффициент корреляции r = 0,584, что говорит о наличии «умеренно сильной» связи между показаниями. Получено уравнение регрессии. На графике линия регрессии расположена ниже разделительной линии, что говорит о «уменьшающем» действии операции на параметр. Если линия регрессии совпадает с диагональю, из левого нижнего угла в правый верхний, то операция не оказывает влияния на параметр, если проходит выше, то операция оказывает «увеличивающее» влияние на параметр, ниже – «уменьшающее».

Величина коэффициента корреляции 0,584, что говорит о значительном влиянии операции на показатели микросхем. Получено уравнение регрессии, представляющее модель, описывающую изменение параметра в результате операции.

103

Глава 3. Методы оценки точности

________________________________________________________________________________

Plot of Fitted Model

Рис. 3.4 График зависимости параметра до и после обработки

Regression Analysis - Linear model: Y = a + b*X

-----------------------------------------------------------------------------

Dependent variable: posleobrabotki Independent variable: doobraboki

-----------------------------------------------------------------------------

-----------------------------------------------------------------------------

-----------------------------------------------------------------------------

Analysis of Variance

-----------------------------------------------------------------------------

Source Sum of Squares Df Mean Square F-Ratio P-Value

-----------------------------------------------------------------------------

-----------------------------------------------------------------------------

Correlation Coefficient = 0,584466

R-squared = 34,16 percent

Standard Error of Est. = 0,564058

The StatAdvisor

---------------

The output shows the results of fitting a linear model to describe the relationship between posleobrabotki and doobraboki. The equation of the fitted model is

posleobrabotki = 3,64636 + 0,458758*doobraboki

Since the P-value in the ANOVA table is less than 0.01, there is a statistically significant relationship between posleobrabotki and doobraboki at the 99% confidence level.

The R-Squared statistic indicates that the model as fitted explains 34,16% of the variability in posleobrabotki. The correlation coefficient equals 0,584466, indicating a moderately strong relationship between the variables. The standard error of the estimate shows the standard deviation of the residuals to be 0,564058. This value can be used to construct prediction limits for new observations by selecting the Forecasts option from the text menu.

104

Раздел I. Методы и средства управления качеством

____________________________________________________________________

3.4.2. Использование корреляционного анализа в многооперационном технологическом процессе

По окончанию технологического процесса сборки приборы подвергают различным технологическим воздействиям, таким как приработка, испытания с имитацией эксплуатационных воздействий (климатических, механических и других). При этом происходит изменение выходного (выходных) параметра и необходимо определить степень влияния денной операции или воздействия на прибор в целом. В этом случае также может быть использован коэффициент корреляции в методике изложенной в [13].

Перепишем выражение для определения коэффициента корреляции в ви-

Например, r используют для исследования передачи погрешности парметра Y (который характеризуется математическим ожиданием М и дисперсией D) с операции n-1 на n.

При этом рассчитывают: коэффициент переноса

105

Раздел I. Методы и средства управления качеством

____________________________________________________________________

тике находят применение пассивные и активные факторные эксперименты. Факторными эксперименты называют потому, что в процессе проведения

эксперимента каким-либо образом изменяют значения первичных параметров, рассматриваемых как факторы, и фиксируют уровень выходного параметра, рассматриваемого как отклик.

При пассивном эксперименте инженер наблюдает значения факторов и регистрирует соответствующий этим значениям уровень выходного параметра (отклика). Изменение значений факторов в таком эксперименте достигается путем замены экземпляра устройства или фиксации изменения технологического параметра. Пассивные эксперименты проводят часто в условиях, когда нет возможности активно вмешиваться в ход технологического процесса. Основной его недостаток состоит также в необходимости проведения большого числа опытов.

При активном эксперименте инженер активно вмешивается в его ход путем принудительной установки (задания) в опытах нужных ему значений факторов. Активные эксперименты позволяют заметно уменьшить количество опытов, требуемое для получения математической модели. Однако их проведение не всегда возможно по техническим или экономическим соображениям.

4.3. Регрессионные модели параметров

При управлении качеством желательно знать не только зависимость друг от друга двух или нескольких количественных признаков, но и вид связи между ними и насколько тесна эта связь. Решение этого вопроса имеет большое значение для контроля и управления качеством объекта.

Связь между двумя количественными признаками проявляется в виде определенной тенденции, например, если один признак увеличивается, то другой увеличивается или уменьшается.

Учитывая, что при статистических связях каждому фиксированному значению одного признака соответствует распределение другого признака, можно представить эту связь в виде зависимости среднего арифметического значения одного признака, например, параметра качества Y от другого признака (признаков, факторов) х.

Корреляционная связь, рассмотренная ранее в разделе 3.4, Y с х выражается в общем виде следующим уравнением:

Уравнение (4.1) называют модельным уравнением регрессии Y на х. Вид функции f(x) в этих уравнениях зависит от формы связи рассматриваемых признаков. Уравнение регрессии отображает форму связи и дает ответ на вопрос, является ли корреляционная связь прямолинейной или криволинейной.

На практике связь между двумя признаками в интересующей области может быть линейной или приблизительной линейной. В тех случаях, когда она нелинейная, часто путем преобразования (логарифмированием, извлечением

107

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

корня и т.д.) одного из признаков можно произвести линеаризацию характера кривой. Кроме того, практически любая нелинейная зависимость может быть разделена на участки с линейной зависимостью рассматриваемых признаков. «Наилучшая» прямая, выравнивающая опытные данные, определяется методом наименьших квадратов.

Если наблюдаемые значения признаков обозначить через (x1, y1), (x2, y2), …, (xn, yn), то прямая регрессии Y на х запишется в виде

арифметическое значений x1, х2, .... xп; Y определяет ординаты точек вычисленной прямой в зависимости от значений признака.

Коэффициент b в уравнении (4.2) называют коэффициентом регрессии Y

i

Коэффициент регрессии Y на х равен тангенсу угла между прямой ре-

грессии и осью x(tg ),

tg b,

Помимо (3.6 ) коэффициент корреляции может быть записан в следующем виде:

При оценке самого коэффициента корреляции учитывается число пар наблюдений n, по которым было произведено его вычисление. При небольшом числе пар величина r часто значительно отличается от его действительного значения. Поэтому нужен критерий, который установит, случайно ли отклоняется коэффициент корреляции от нуля или имеется корреляционная связь.

Для этого вычисляют

и оценивают полученное значение t с числом степеней свободы v = n – 2. Если t tT (табл. [7]), то корреляция между рассматриваемыми признаками существует.

Так как число наблюдений n ограничено, то на практике возникает вопрос, насколько правомерно в дальнейших инженерных расчетах можно пользоваться полученной оценкой коэффициента корреляции.

Для ответа на него выполняют проверку статистической значимости (в дальнейшем просто значимости). Это означает выяснение, за счет чего оценка коэффициента корреляции оказалось отличной от нуля: за счет ограниченности числа

108

Раздел I. Методы и средства управления качеством

____________________________________________________________________

наблюдений, т.е. случайных причин, либо за счет того, что это объективно имеет место.

Проверку значимости коэффициента корреляции выполняют по-разному, в зависимости от числа наблюдений пар параметров. При числе наблюдений n > 50 принимают гипотезу о нормальном распределении оценки r* , поскольку доказано, что при n > 50 эта гипотеза, как правило, работает. Затем строят доверительный интервал, симметричный относительно рассчитанной точечной оценки r*. Для коэффициента корреляции его определяют как

t – коэффициент, зависящий от доверительной вероятности .

Построив доверительный интервал, проверяют, попадает ли в этот интервал точка r = 0. Если да, то нет оснований оценку коэффициента корреляции считать значимой, ибо отличной от нуля с вероятностью она оказалась за счет ограниченного числа наблюдений.

На выходные параметры изделий или техпроцессов оказывают влияние большое число первичных параметров. Часть первичных параметров мы знаем, а о влиянии некоторых из них даже не догадываемся. При решении инженерных задач ограничиваются небольшим числом наиболее существенных первичных параметров. Обычно это число k 5–8. В связи с этим зависимость выходного параметра Y от учитываемых первичных параметров x1, …, xk оказывается вероятностной. Тогда корреляционное поле параметров х и Y может, например, принять вид, показанный на рис. 3.1 .

Проведем в корреляционном поле прямую или кривую линию, которая лучшим образом характеризует изменение выходного параметра Y в зависимости от первичного параметра х. Эту линию называют линией регрессии, а математическое выражение, описывающее линию – уравнением регрессии или регрессионной моделью. Когда первичный параметр не один, а несколько, то говорят об уравнении множественной регрессии.

В инженерной практике популярны регрессионные модели в виде полиномов. Особый интерес представляет полином первой степени. Его математический вид

i 1

где Y – выходной параметр РЭУ или ТП; x1,…xk – первичные параметры;

n – число учитываемых первичных параметров;

a0,a1,…,ak – коэффициенты модели, определяемые по результатам экспериментов.

Модель вида (4.8) называют также уравнением множественной линейной регрессии.

109

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

К математическим моделям предъявляются два основных требования [4]: простота получения и относительно минимальные погрешности при опи-

сании поведения устройства или процесса. Во многом этим требованиям отвечают линейные регрессионные модели вида (4.8). Для определения по данным эксперимента коэффициентов a0, a1,…ak могут быть использованы несложные расчетные формулы, а удовлетворительность описания реальных изделий и ТП обусловлена небольшим отклонением первичных параметров относительно своих средних (номинальных) значений, составляющий обычно не более 20…30%. Из рис. 1.9. видно, что замена нелинейной зависимости на участке xном ± x прямой линией не вызовет больших ошибок. По этой причине линейные регрессионные модели в большинстве случаев оказываются пригодными для дальнейшего инженерного анализа приборов или ТП их изготовления.

При построении математических моделей возникает вопрос, как в корреляционном поле лучшим образом провести прямую или другую линию. Для ответа на этот вопрос используется метод наименьших квадратов.

4.4. Метод наименьших квадратов

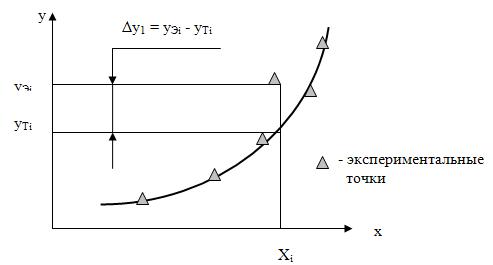
Пусть в результате эксперимента для наблюдаемых значений первичного параметра хi зафиксированы значения выходного параметра Y. Нанесем результаты эксперимента в виде экспериментальных точек на координатную плоскость (рис. 4.1).

Рис. 4.1. К использованию метода наименьших квадратов

Понятно, что лучшей линией в корреляционном поле является такая, для которой расхождение с экспериментальными точками минимально. Это можно записать в виде критерия

где n – число экспериментальных точек (точек корреляционного поля); yЭi – экспериментальное значение у в i-й точке; yТi – теоретическое значение у в i-й

110