Управление качеством в приборостроении

Раздел I. Методы и средства управления качеством

____________________________________________________________________

точке. Для получения значения ут, нужно в математическое выражение, описывающее предполагаемую удачную линию, подставить значение xi. Критерий вида (4.9) является общим критерием. На его основе могут быть предложены конкретные критерии, а именно:

маются со своим знаком, поэтому по математической записи он совпадает с общим критерием (4.9).

Из указанных критериев выбирают критерий (4.12) при значении = 2,

i 1

Подбор теоретических линий (функций) на его основе получил название метода наименьших квадратов. Этот метод имеет веское теоретическое обоснование ввиду следующего:

линия, построенная в корреляционном поле с помощью данного метода, является наиболее вероятной;

метод приводит к получению простых расчетных формул для определения коэффициентов теоретических функций.

4.5. Применение пассивного эксперимента для получения математических моделей

Опишем основные этапы процедуры получения математических моделей объектов с использованием пассивных экспериментов.

1.Для рассматриваемого вида устройства выявляются первичные параметры (факторы), в наибольшей степени влияющие на выходной параметр. Число этих факторов k рекомендуется ограничивать значением k ≤ 5–8.

2.Определяется требуемое количество опытов пассивного эксперимента n или, что то же самое, требуемое число замен экземпляра устройства:

где – минимальное значение коэффициента парной корреляции между первичным параметром (фактором) и выходным параметром, считаемое еще значимым (существенным, весомым); обычно |rmin| = 0,2…0,3;

r – среднее квадратичное отклонение коэффициента корреляции.

111

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

Значение r, определяют, как

где ty — коэффициент, зависящий от доверительной вероятности γ.

Пример 4.1. Требуется определить, какое число опытов пассивного эксперимента необходимо провести для случая, когда принято значение |rmin| = 0,3. Доверительная вероятность y = 0,95.

Решение. По табл. [7] для у = 0,95 находим ty = 1,96. По формуле (4.15) вычислим значение r:

r 1,960,3 0,153

Используя выражение (4.14), определим требуемое число опытов:

Нетрудно убедиться, что для |rmin|= 0,2 число опытов n 89.

3.Проводятся опыты пассивного эксперимента. Проведение опытов включает:

•наблюдение (измерение) значений факторов для исследуемого экземпляра устройства или техпроцесса;

•регистрацию (измерение) значения выходного параметра, соответствующего наблюдаемым значениям факторов;

•замену экземпляра устройства или фиксация параметра с другим технологическим режимом.

4.Выполняется статистическая обработка результатов опытов. В общем случае сложность математической обработки зависит от того, коррелированны ли между собой факторы.

Статистическая обработка в настоящее время как правило выполняется на ЭВМ с использованием библиотечных программ [5,14,22].

По результатам статистической обработки строят модели в виде уравнения регрессии. Часто вначале строят линейную модель

k – количество факторов, принятых во внимание;

a0, a1,…,ak – коэффициенты модели, получаемые из эксперимента.

При записи математической модели в нее включают только значимые коэффициенты. Проверка значимости, как правило, является составной частью статистической обработки и выполняется с помощью тех же библиотечных программ.

Проверить значимость коэффициента модели означает дать ответ на вопрос, за счет чего коэффициент оказался отличным от нуля – за счет случайных причин (ограниченного числа опытов), либо за счет того, что это объективно

112

Раздел I. Методы и средства управления качеством

____________________________________________________________________

имеет место.

Программы для ЭВМ, выполняющие процедуру проверки значимости, реализуют обычно следующий алгоритм. Для рассматриваемого коэффициента,

например а, определяется доверительный интервал (интервальная оценка) I(ya ) , соответствующий доверительной вероятности γ:

I(ya) {aH ; aB},

где aH, aB – границы интервала.

Далее уточняется вопрос, попадает ли в построенный доверительный интервал I(ya ) точка a = 0 (рис. 4.2).

Рис. 4.2. Доверительный интервал для коэффициента а; аточ – точечная оценка.

Если это происходит, то нет оснований точечную оценку a* , полученную при статистической обработке, считать значимой, ибо отличной от нуля она могла оказаться за счет ограниченности числа опытов, погрешностей эксперимента и других случайных причин. Следовательно, такой коэффициент (слагаемое с коэффициентом а*) не следует включать в формируемую математическую модель.

Если в дальнейшем выяснится, что линейная модель вида (4.16) окажется неадекватной результатам эксперимента, то опять-таки с использованием библиотечных программ для ЭВМ, строят математическую модель в виде степенного полинома. Обычно ограничиваются полиномом второй, реже третьей степени.

5. Проверяется пригодность построенной модели для целей практики. Об этом судят по ее адекватности результатам эксперимента.

Проверить адекватность модели означает выяснить вопрос, за счет чего имеют место расхождения между значениями выходного параметра, полученными экспериментально и подсчитанными по построенной математической модели, – за счет погрешностей в опытах либо за счет того, что модель плохо описывает поведение выходного параметра объекта. Обычно этап 5 выполняют также на ЭВМ, совместно с этапом 4.

Многие библиотечные программы при проверке адекватности используют критерий Фишера.

4.6. Отбор информативных параметров, характеризующих качество изготовления изделий

Задача выбора информативных параметров изделий возникает как при подготовке к проведению пассивных экспериментов, так и при контроле их в

113

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

ходе технологического процесса, а также при проведении мероприятий по управлению качеством продукции. Например, в производстве полупроводниковых приборов трудоемкость контрольно – измерительных операций составляет 30…50% общей трудоемкости. Одной из причин этого является необоснованно большое количество измеряемых параметров и режимов.

Аналогичная проблема возникает при построении статистических моделей объектов и техпроцессов. Обычно исследователю достаточно хорошо известен набор технологических факторов и интервалы их изменения. Однако такая ситуация изменяется при освоении новых изделий и технологических процессов.

Как уже было указано ранее, первичные факторы могут быть количественные и качественные. В последнем случае обычно используют метод экспертных оценок, базирующийся на математической обработке опыта и интуиции экспертов в данной области.

Данная задача относится к проблемам многомерного статистического анализа, который представляет собой раздел, посвященный систематизации и обработке многомерных данных, направленных на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака для получения научных и практических результатов.

Многомерный анализ содержит следующие основные процедуры: метод главных компонент; факторный анализ; кластерный анализ; дискриминантный анализ; канонический корреляционный анализ.

Использование диаграммы Парето.

Диаграмма Парето названа по имени итальянского экономиста Парето (1845–1923). Она широко применяется как один из семи основных методов контроля качества [8, 20].

Вповседневной деятельности по контролю и управлению качеством постоянно возникают всевозможные проблемы, связанные, например, с появлением брака, неполадками оборудования, увеличением времени от выпуска партии изделий до ее сбыта, наличием на складе нереализованной продукции, поступлением рекламаций.

Диаграмма Парето позволяет распределить усилия для разрешения возникающих проблем и установить основные факторы, с которых нужно начинать действовать с целью преодоления возникающих проблем. Построение диаграммы Парето начинают с классификации возникающих проблем по отдельным факторам (например, проблемы, относящиеся к браку; проблемы, относящиеся к работе оборудования или исполнителей, и т. д.). Затем производят сбор

ианализ статистического материала по каждому фактору, чтобы выяснить, какие из этих факторов являются превалирующими при решении проблем.

Впрямоугольной системе координат по оси абсцисс откладывают равные отрезки, соответствующие рассматриваемым факторам, а по оси ординат

— величину их вклада в решаемую проблему. При этом порядок расположения факторов таков, что влияние каждого последующего фактора, расположенного по оси абсцисс, уменьшается по сравнению с предыдущим фактором (или

114

Раздел I. Методы и средства управления качеством

____________________________________________________________________

группой факторов). В результате получается диаграмма в виде столбчатого графика, столбики которого соответствуют отдельным факторам, являющимся причинами возникновения проблемы, и высота столбиков уменьшается слева направо, как показано ниже, на рис. в примере.

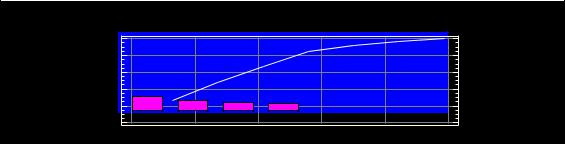
Суммируя последовательно высоту всех столбиков гистограммы, строим ломаную кумулятивную кривую, которая называется кривой Парето или диаграммой Парето . Использование диаграммы Парето показано в разделе 4.6. Ниже приведена диаграмма Парето, построенная для примера [20], где даны причины брака микросхем (в таблице перечислены в кодированном виде различные причины брака). Использованы следующие обозначения дефектов: 1- герметизация, 2- диффузия, 3 – металлизация, 4 – припайка, 5 – осаждение диэлектрика, 6 – разварка выводов, 7 – фотолитография.

В результате анализа данных с помощью диаграммы Парето получено следующее распределение дефектов по величине их вклада в общий объем брака: 4 – припайка (26%), 1 – герметизация (22%), 6 – разварка выводов ( 19%), 7

–фотолитография (18%), 5 – осаждение диэлектрика (7%), 2 – диффузия (5%), 3

–металлизация (3%).

115

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

Pareto Chart for brakMS

Рис. 4.3. Диаграмма Парето для анализа причин брака при производстве микросхем (brakMS)

Причинно-следственная диаграмма.

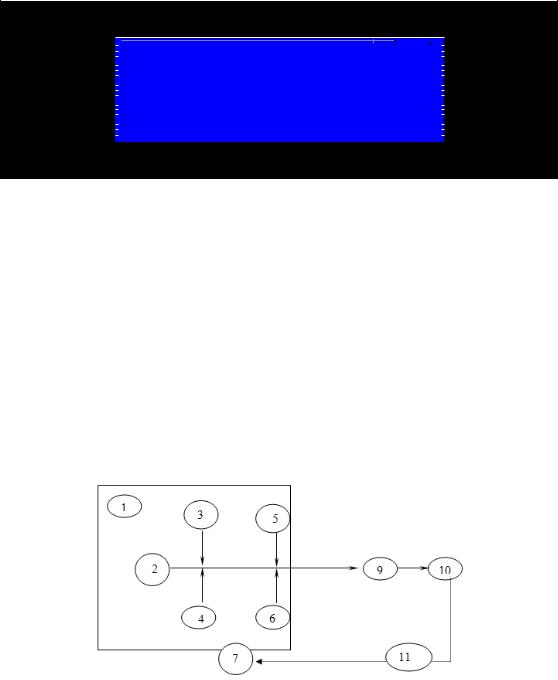
Как уже ранее отмечалось, качество изделий обеспечивается в процессе их изготовления и является результатом действия системы факторов и причин, составляющих процесс. Все многообразие факторов и причин, составляющих технологический процесс, можно расслаивать с помощью метода 4М (см. 3.1). Поэтому процесс изготовления изделий, влияющий на качество изделия, можно рассматривать как взаимодействие 4М. Зависимость между процессом 4М, представляющим собой систему причинных факторов, и качеством, представляющим собой результат действия этих причинных факторов, можно выразить графически, как показано на рис. 4.4

Рис. 4.4. Причинно-следственная диаграмма:

1 – система причинных факторов; 2 – основные факторы производства; 3 – материалы; 4 – оператор; 5 – оборудование, включая инструменты; 6 – методы операций; 7 – процесс 4М; 8 – следствие; 9 – параметры качества; 10 – показатели качества; 11 – процесс контроля качества

Если в результате процесса качество изделия оказалось неудовлетворительным, значит в системе причин, т. е. в какой-то точке процесса, произошло отклонение от заданных условий. Если эта причина может быть обнаружена и устранена, то будут производиться изделия только высокого качества. Более того, если постоянно поддерживать заданные условия хода процесса, то можно обеспечить формирование высокого качества выпускаемых изделий. Важно также, что полученный результат – показатели качества (точность размеров, степень чистоты, значение электрических величин и т.д.) – выражается кон-

116

Раздел I. Методы и средства управления качеством

____________________________________________________________________

кретными данными (поз. 10 на рис. 4.4). Используя эти данные, с помощью статистических методов осуществляют контроль процесса, т.е. проверяют систему причинных факторов. Таким образом, процесс контролируется по фактору качества (поз. 11 на рис. 4.4).

Для производства качественных изделий необходимо наиболее важным показателям качества (являющимся следствием) поставить в соответствие различные факторы производства (составляющие систему причинных факторов). Затем через воздействие на отрицательные факторы правильно подобранными мерами процесс вводят в стабильное состояние. Для этого важно хорошо понимать и контролировать зависимость между характеристиками качества (следствием) и параметрами процесса (системой причинныx факторов). При этом удобно использовать причинно-следственную диаграмму, приведенную на рис. 4.5, которую из-за своего внешнего вида часто называют «рыбьей костью» или «рыбьим скелетом». Как показано на рис. 4.5, показатели качества, являющиеся «хребтом» этого скелета и в то же время следствием (результатом) различных причин (факторов), – причины 1, причины 2 и т. д. На рис. 4.5 они обозначены стрелками, которые называют «большими костями». Эти причины являются, в свою очередь, следствием других причин: A1 A2, ... (для следствия А); В1 ,В2 , ... (для следствия В) и т. д. («средние кости»). Все они также обозначены стрелками, направленными к соответствующим следствиям. Вторичным причинам могут соответствовать третичные причины и т. д. («малые кости»).

Рис. 4.5. Причинно–следственная диаграмма (рыбья кость)

При поиске причин важно помнить, что показатели качества, являющиеся следствием процесса, обязательно испытывают разброс. Поиск факторов, оказывающих особенно большое влияние на разброс показателей качества изделия (т.е. на результат), называют исследованием причин.

Таким образом, причинно-следственная диаграмма позволяет выявить и систематизировать различные факторы и условия (например, исходные материалы, условия операций, станки и оборудование, операторы), оказывающие влияние на рассматриваемую проблему (на показатели качества). Информация о показателях качества для построения диаграммы собирается из всех доступных источников: используются журнал регистрации операций, журнал регистрации данных текущего контроля, сообщения рабочих производственного участка и т. д. При построении диаграммы выбираются наиболее важные с технической

117

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

точки зрения факторы. Для этой цели широко используется экспертная оценка. Очень важно проследить корреляционную зависимость между причинными факторами, (параметрами процесса) и показателями качества. В этом случае параметры легко поддаются корреляции. Для этого при анализе дефектов изделий их следует разделить на случайные и систематические, обратив особое внимание на возможность выявления и последующего устранения в первую очередь причины систематических дефектов.

Сложная причинно-следственная диаграмма анализируется с помощью расслоения по обязательным факторам, таким, как материалы, исполнители, время проведения операций и др. При выявленной заметной разнице в разбросе принимают соответствующие меры для ликвидации причины ее появления. В результате должны остаться только случайные дефекты, уменьшить число которых значительно сложнее, но также возможно с помощью причинноследственной диаграммы. Рекомендуют такую последовательность ее построе-

ния [23]:

1.За заданный срок собрать данные, которые могут иметь отношение к браку, выявить количество видов дефектов и подсчитать сумму потерь, соответствующую каждому из видов.

2.С помощью диаграммы Парето оцепить вклад каждого вида, в первую очередь систематических дефектов, в суммарный брак изделий.

3.Выявить этапы возникновения дефектов.

4.Построить причинно-следственную диаграмму выбранных групп дефектов.

5.Рассортировать причины на устранимые, трудно устранимые и неустранимые.

6.Подготовить и реализовать план мероприятий по исключению устранимых и уменьшению влияния трудно устранимых причин.

7.Собрать данные (за определенный срок после выполнения плана мероприятия), имеющие отношение к браку изделий; подсчитать сумму потерь, соответствующую каждому из этих, видов дефектов.

8.Построить вновь диаграмму Парето и проверить эффективность проведенных улучшений.

4.7. Получение математических моделей с помощью активных факторных экспериментов

4.7.1.Задачи теории планирования эксперимента

Винженерной практике стремятся получить математические модели изделий или технологических процессов с использованием минимального числа опытов. В ряде случаев это можно сделать с помощью математической теории планирования эксперимента.

Планирование эксперимента — это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

118

Раздел I. Методы и средства управления качеством

____________________________________________________________________

В теории планирования эксперимента процедуру выбора числа и условий проведения опытов называют планированием многофакторного эксперимента, имея в виду, что число факторов — не менее двух. Термин "варьирование" означает установление исследователем нужных ему в эксперименте значений (уровней) факторов.

Теория планирования эксперимента должна дать ответы на следующие вопросы:

•по какому плану проводить эксперимент;

•как обрабатывать результаты эксперимента;

•как оценивать качество опытов и пригодность построенной модели для практики?

4.7.2. Основы теории планирования активных факторных экспериментов

Пусть факторы х1, ..., хk объекта исследования связаны с выходным параметром (откликом) зависимостью

где k — число учитываемых факторов.

При использовании полных факторных экспериментов (ПФЭ) зависимость (3.22) часто получают в виде неполной квадратичной модели (полинома):

где 0 , 1,..., k , 12 ,... – коэффициенты полинома;

x1,…x2 – натуральные (в своей размерности) значения факторов. Многоточие в конце выражения (4.18) означает, что на практике можно

интересоваться не всеми взаимодействиями (произведениями) факторов, а лишь линейной частью модели.

Модель вида (4.18) называют уравнением регрессии, или регрессионной моделью, коэффициенты 0 , 1,..., k , 12 ,...— коэффициентами регрессионной

модели.

Получить полином с натуральными значениями факторов (размерный полином) сразу в большинстве случаев не представляется возможным. Поэтому вначале получают полином с кодированными безразмерными значениями факторов. Такой полином будем называть безразмерным.

Безразмерный полином ищут в виде

где x1,...,x k – кодированные (безразмерные) значения факторов;

b0, b1 ... – коэффициенты, значения которых в общем случае отличны от значений аналогичных коэффициентов модели (4.18).

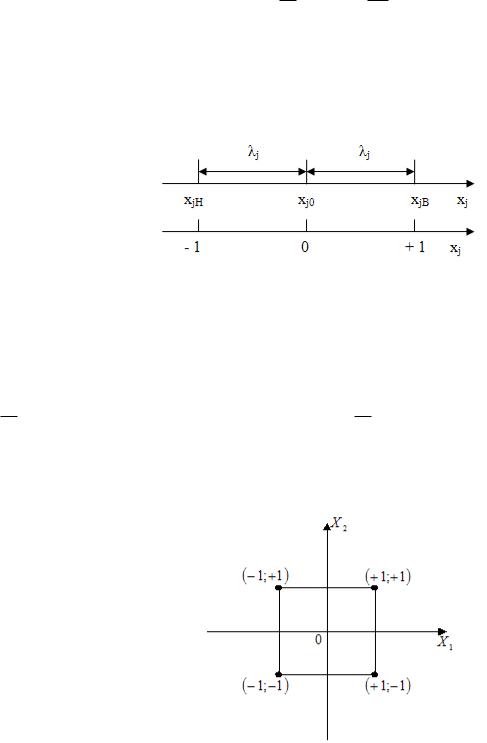
Кодированные значения факторов определяются соотношением

119

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

где хj – натуральное текущее значение j-го фактора;

хjо – натуральное значение нулевого уровня j-го фактора;

j – половина размаха варьирования j-го фактора, называется обычно ин-

каждый фактор достаточно варьировать на двух уровнях. Уровень j-го фактора, соответствующий большему значению xjB, называют верхним, а соответствующий меньшему значению xjH – нижним.

Посредине между ними размещен основной (нулевой или базовый) уровень (рис. 4.6).

Рис. 4.6 Уровни варьирования фактора xi

При кодировании уровней факторов с использованием выражения (4.20)

x j 1соответствует нижнему, а значение x j 1 – верхнему уровням варьи-

рования (рис. 4.7). В дальнейшем будут рассмотрены эксперименты, в которых кодированные уровни факторов принимают значения –1 или +1.

120