Управление качеством в приборостроении

Раздел I. Методы и средства управления качеством

____________________________________________________________________

фекты взаимодействия, а линейная модель неадекватно описывает технологический процесс Fрасч 32 Fтабл . Это позволяет сделать вывод о том, что мы приблизились к почти стационарной области. Для изучения этой области применяем центральное композиционное ортогональное планирование, матрица которого получена добавлением к матрице ПФЭ (последней) нескольких специально спланированных экспериментальных точек (табл. 12).

Таблица 12

131

Глава 4. Математические модели изделий и технологических процессов

________________________________________________________________________________

В результате обработки матрицы ортогонального планирования при по-

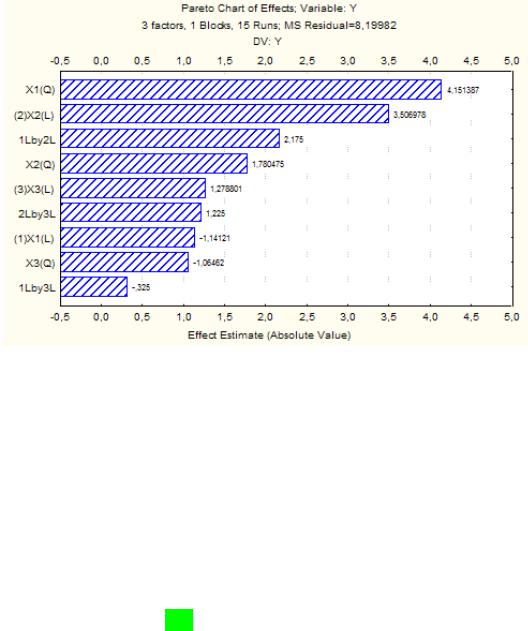
Полученная экспериментально-статистическая модель позволяет с вероятностью 0,95 утверждать, что на прочность соединений при ультразвуковой сварке влияет амплитуда сварочного наконечника – электрода. Влияние остальных факторов и их взаимодействий незначительно.

Переход от кодированных значений к натуральным величинам проводится при помощи уравнения (2).

132

Раздел I. Методы и средства управления качеством

____________________________________________________________________

ГЛАВА 5 ОЦЕНКА СТАБИЛЬНОСТИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

5.1. Основные задачи оценки стабильности

Стабильность является важнейшим составляющим понятия качества приборов или технологических процессов (для упрощения будем в дальнейшем использовать понятие техпроцесс, хотя рассмотренные методы применимы и к анализу стабильности производимых изделий). От стабильности зависит надежность, экономические показатели, качество производимых изделий в целом.

Стабильность техпроцесса – это свойство, характеризующее постоянство параметров в условиях воздействий технологических погрешностей, дестабилизирующих факторов, износов и старения. При этом подразумевается неизменность параметров относительно своего начального значения и неизменность закона распределения.

Используется так же понятие устойчивость – свойство сохранять точность параметров во времени. Процесс может быть устойчивым, но не стабильным, когда его параметры изменяются с течением времени по какому то закону.

Понятие стабильности аналогично понятию надежности техпроцесса, т.к. и в том и в другом случае оценивается изменение точности во времени. С учетом фактора времени можно рассматривать стабильность для:

•быстро протекающих процессов ( исчисляемых секундами и минутами) -

•вибрации, колебания параметров источников питания и др. Для оценки стабильности используют выборки (экспериментальные партии), характеризующиеся мгновенным распределением, когда исследуется изменение параметра x за малый промежуток времени ∆t;

•процессы средней скорости (например, износ резца), эти процессы характеризуются длительностью в минутах и часах;

•медленно протекающие процессы (например, износ оборудования). В последних двух случаях используется понятие полного распределения, за какой то значительный период времени.

Вобщем случае для разных типов технологического оборудования стабильность различается в больших пределах. Так время работы до износа сверла при сверлении печатных плат - в пределах десяти минут, а стабильность прессовых операций или литья может характеризоваться часами и сменами.

Для рассмотрения особенностей проблемы стабильности технологических процессов используем графическое изображение поля допуска и поля рассеивания с помощью точностной диаграммы. При этом возможны следующие варианты.

•распределение гауссовское, среднее значение и дисперсия постоянны;

•если время работы оборудования нельзя считать пренебрежимо малым, то следует ожидать увеличения дисперсии параметров;

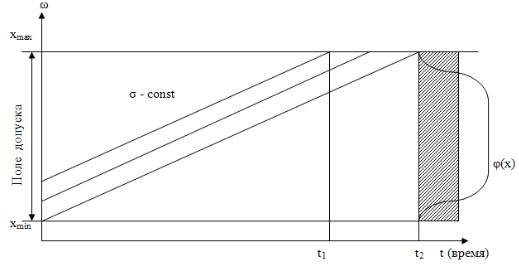
•из-за наличия систематических закономерно изменяющихся погрешностей происходит смещение центра настройки (рис. 5.1), необходимо

133

Глава 5. Оценка стабильности технологических процессов

________________________________________________________________________________

определить время подналадки.

Рис. 5.1. Изменение точности во времени

По ГОСТ 16304-74 для оценки точности и стабильности используют следующие показатели.

1. Коэффициент точности относительно номинального значения параметра, выраженный отношением погрешности значения параметра к номинальному значению параметра xn

где xд – действительное значение параметра.

2. Коэффициент точности относительно поля допуска

настройки; x1 - среднее значение первой мгновенной выборки после настройки станка; - поле допуска,

значение последней перед новой настройкой мгновенной выборки.

134

Глава 5. Оценка стабильности технологических процессов

________________________________________________________________________________

мых оценок дисперсий генеральной совокупности S12 и S22 , имеющих соответ-

ственно степени свободы ν1 и ν2, т.е. F = S12 / S22.

При этом должно выполняться условие S12 > S22 в противном случае следует поменять местами выборочные дисперсии. Найденное экспериментальное значение F сравнивается с теоретическим Ft которое по числу степеней свободы

и при заданном значении коэффициента риска находится из табл. [ 7], постро-

енной для F-распределения обладающего тем свойством, что случайные значения отношений дисперсий двух независимых выборок будут не менее F, по сравнению с заданным коэффициентом риска β. Для практических целей достаточно иметь такие таблицы для β = 0,01 и β = 0,05. Например, β = 0,01 (1%)

означает, что отклонения, равного или большего наблюдаемого, можно ожидать только один раз на 100 опытов. Такая малая вероятность указывает на высокую степень значимости. Вот почему иногда вместо коэффициента риска эту вероятность называют уровнем значимости. В [2] предлагается использовать значение z0 = 1,15 lg S12 / S22, где

В тех случаях, когда объемы всех выборок, по которым вычислялись дисперсии, одинаковы, для оценки однородности дисперсий целесообразно использовать критерий Кохрена, который предложил рассматривать отношение максимальной дисперсии к сумме всех остальных:

Квантили для величин g приведены в [ 7]. Таблица имеет два входа: р – число выборочных значений Si2, k = n – 1 – число степеней свободы.

Пример 5.1. Исследовалась стабильность работы станка, объем выборки 20 штук. Дисперсия и среднее значение параметра в начале смены: Dн = 1,39;

Хн = 3,15; в конце Dк = 1,14; Хк = 7,0. По таблицам [7], для 95% уровня значимо-

сти т.к. Fэ < Fт (1,22 < 2,2), то нет оснований считать процесс нестабильным.

5.2.2. Критерий Стьюдента (t-критерий)

Для проверки гипотезы о равенстве двух выборочных средних значений случайной величины, имеющей гауссовский закон распределения, используется критерий Стъюдента.

Найденное экспериментальное значение t сравнивают с табличным, которое определяют по таблице распределения Стьюдента. При заданном значении коэффициента риска b число степеней свободы v определяет значение t, по строке. Если t tт, тo гипотеза о равенстве выборочных средних арифметических значений принимается, а это значит, что выборки взяты из одной и той же генеральной совокупности. В заключение следует отметить, что при малом

136

Раздел I. Методы и средства управления качеством

____________________________________________________________________

объеме выборки (n < 10), t – случайная величина и ее распределение не является гауссовским. Однако по мере увеличения объема выборки t – pacпределение приближается к гауссовскому. При n 30 его можно считать практическим гауссовским и оно не отличается от нормального распределения.

Пример 5.2. Используя данные предыдущего примера определяем, что tэ = 10,56, а tт = 2,02. Следовательно, доказано наличие систематических ошибок.

5.3. Определение периода подналадки оборудования

При обработке на настроенном оборудовании под влиянием случайных и систематических погрешностей происходит смещение уровня настройки x(t) и увеличение мгновенного поля рассеивания ωр(t), что может привести к появлению брака. Для восстановления точности необходимо произвести подналадку, определить момент проведения подналадки.

Данный метод используют, когда известны функции x и . Известно, что мгновенное распределение размеров является всегда гауссовским, тогда

p(t) = 3 (t).

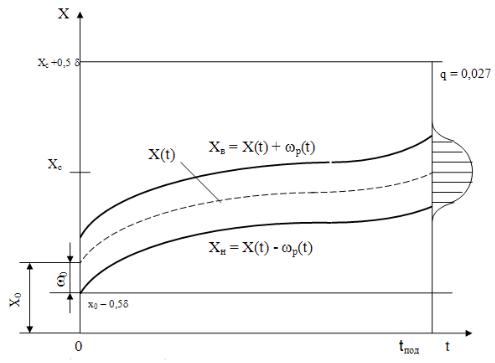
Из рис. 5.2 видно, что поднастройку нужно производить для условий

Xc X(t) p (t)

Xc X(t) p (t).

Рис. 5.2. К определению периода подналадки

Рассмотрим случай, когда смещение уровня настройки описывается степенной функцией

X(t) X0 Vt1n ;p (t) 0 const,

137

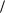
Глава 5. Оценка стабильности технологических процессов

________________________________________________________________________________

отсюда

Xc X0 Vt1подn 0 ,

откуда

Если время на 1 деталь t = 34 с, то за это время будет изготовлено 58 деталей.

5.4. Анализ временных рядов для оценки стабильности

Многие экспериментальные данные представляют собой временные последовательности. В настоящее время существует большое количество стандартных программ, позволяющих автоматизировать анализ, анализировать временные последовательности с помощью разнообразных современных математических методов. К ним относятся:

•описательные методы: график временного ряда, автокорреляция, периодограмма, тест рандомизации, кросс-корреляция;

•сглаживание, позволяющее демпфировать вариации временного ряда;

•прогнозирование.

5.5. Контрольные карты

Для оценки стабильности технологических процессов наряду с вышерассмотренными методами широко применяются контрольные карты. Их главным достоинством является возможность оперативно, на рабочем месте без выполнения трудоемких математических вычислений оценивать стабильность.

Контрольные карты – инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него ( с помощью соответствующей обратной связи), предупреждая его отклонения от предъявляемых к процессу требований.

Наиболее широко используются следующие типы контрольных карт:

•средних арифметических и размахов (X – R );

•медиан и размахов (Ме – R);

138

Раздел I. Методы и средства управления качеством

____________________________________________________________________

•индивидуальных значений (х);

•доли дефектной продукции (р);

•числа дефектных единиц продукции (рп );

•числа дефектов (с);

•числа дефектов на единицу продукции (и).

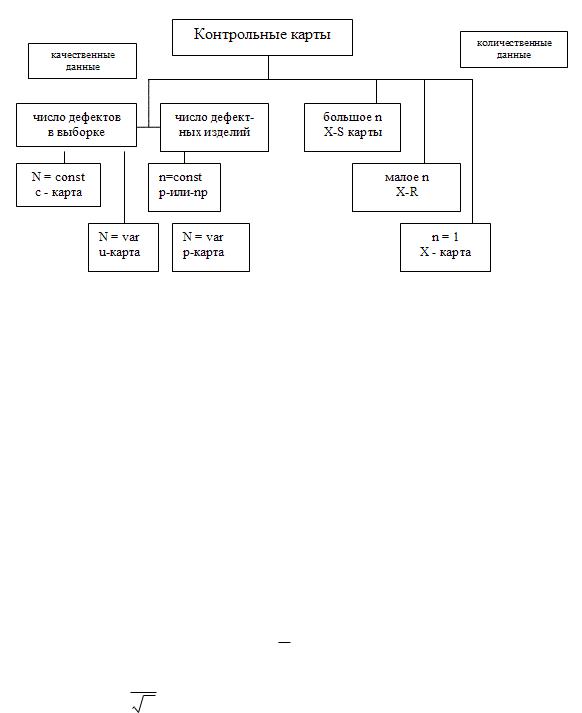
Перечисленные карты относятся к категории карт Шухарта, которые широко применяются в Японии и Европе. Эти карты показывают текущее состояние процесса, но не показывают тенденции. В Америке используют кумулятивные карты, показывающие к чему стремится процесс. Существующие разновидности контрольных карт показаны на следующей схеме.

Рис. 5.3. Типы контрольных карт.

При использовании контрольных карт процесс считается контролируемым, если систематические составляющие его погрешности регулярно выявляются и устраняются, а остаются только случайные составляющие погрешностей, которые, как правило, распределяются в соответствии с нормальным законом.

Основной проблемой при использовании контрольных карт является вычисление границ регулирования, т.е. пределов в которых должен находится стабильный технологический процесс. Методика их определения изложена в отечественных и зарубежных нормативных документах. В качестве примера покажем последовательность определения границ регулирования для Х-карты.

Если известны математическое ожидание и дисперсия контролируемой генеральной совокупности (эти параметры могут быть заданы на технологический процесс), то верхняя и нижняя границы регулирования для Х-карты при доверительной вероятности 0,9973 откладываются от математического ожида-

ния (средней линии) на расстоянии 3 n .

M(x) 3n M(x) A KВ – верхняя граница регулирова-

ния.

139

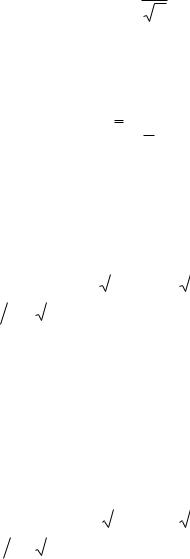
Глава 5. Оценка стабильности технологических процессов

________________________________________________________________________________

Аналогично определяется и нижняя граница

M(x) 3n M(x) A KH .

Если математическое ожидание генеральной совокупности не известно, то для построения средней линии находят оценку математического ожидания – общую среднюю арифметическую Х , вычисляемую по k значениям выборочных средних хi:

1 k

xk i 1xi .

Вэтом случае из текущего процесса отбирают как можно больше выбо-

рок ( k = 20...30) объемом n.

Если неизвестно стандартное отклонение σ генеральной совокупности, то его можно оценить с помощью среднего выборочного значения s по формуле

По известным s и С2 легко вычисляются границы регулирования для х- карты:

Коэффициенты А1 и С2 зависят от объема выборок Неизвестное стандартное отклонение σ генеральной совокупности можно

оценить с помощью средней величины размаха R:

Тогда границы регулирования для х-карты вычисляются следующим образом:

Чтобы получить более полное представление о ходе производственного

процесса, наряду с х-картой ведут либо s-карту, с помощью которой непрерывно контролируют стандартное отклонение, либо R-карту для контроля размахов выборок. При этом создание контрольных карт обычно начинают с изготовления карт для стандартных отклонений или размахов, а не с контрольных карт для средних, ибо к моменту начала контроля производства имеется мало исходных данных (или вообще не имеется) для оценки σ и, следовательно, для создания х-карты.

Для иллюстрации методов рассмотрим несколько примеров.

140