Управление качеством в приборостроении

Раздел I. Методы и средства управления качеством

____________________________________________________________________

а четвертый момент - эксцесс или островершинность:

2.4. Закон нормального распределения (закон Гаусса)

Обычно ожидают, что распределение погрешностей характеризуется законом нормального распределения (ЗНР). Условия его появления следующие:

•погрешностей много (более 5...10);

•среди погрешностей нет доминирующих (значительно отличающихся по величине);

•погрешности «более – менее» стабильны во времени.

Такие условия имеют место чаще всего, по этому такой закон называется «нормальным». Например, такое распределение будет иметь место для таких показателей как вес, рост, возраст группы студентов, т.к. для каждого студента эти величины разные (первое условие), среди них нет доминирующих (студентов имеющих аномальные антропометрические показатели, или возраст более тридцати лет и т.д.) – второе условие, перечисленные характеристики группы можно считать стабильными в момент исследования, хотя через какой то период они естественно изменятся.

Функция f(x) для этой модели имеет вид

где x – рассматриваемый параметр и его текущие значения; m, – параметры модели.

Функция распределения для нормальной модели может быть получена в виде

Указанный интеграл нельзя выразить через элементарные функции. Для его определения используют специальные табличные функции. В инженерной практике широко используют две:

0, = 1 (в дальнейшем – функция стандартного нормального распределения);

81

Глава 2. Статистические методы контроля и управления качеством продукции

________________________________________________________________________________

С учетом выражения (2.6) вероятность вида Р(а . х . b) может быть определена как

С параметрами m и нормальной модели связаны числовые характеристики M(x) и (x). Для нормальной модели, и только для нее, справедливы равенства

m M(x),

(x).

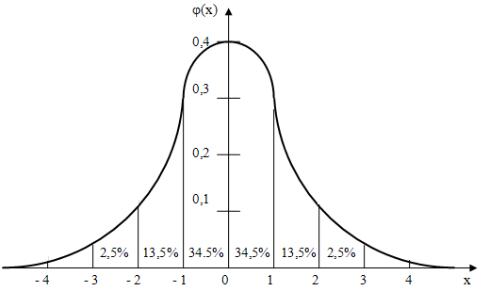
Графики функций f(x) и F(x) приведены на рис. 2.4.

Рис. 2.4. Графики функций f(x) и F(x) для нормальной модели

В случае нормальной модели может интересовать вопрос, какова вероятность вида

где n = 1, 2, 3,… - целые числа.

Применяя выражение (2.15), для n = 1, 2, 3 получим значения, приведенные в табл. 2.1.

82

Раздел I. Методы и средства управления качеством

____________________________________________________________________

Таблица 2.1 Значения вероятностей P(m – n x m + n ) в зависимости от n

Из табл. 2.1. видно, что в диапазон (m – 3 ; m + 3 ) укладывается практически все рассеивание параметра (99,73% значений). Поэтому на практике, определив параметры нормальной модели, предельными значениями рассматриваемого параметра считают точки, отстоящие от величины m на 3 (рис. 2.5). Такой способ оценки предельных отклонений параметра получил название «правила трех сигм». Этим правилом широко пользуются при установлении допусков на параметры.

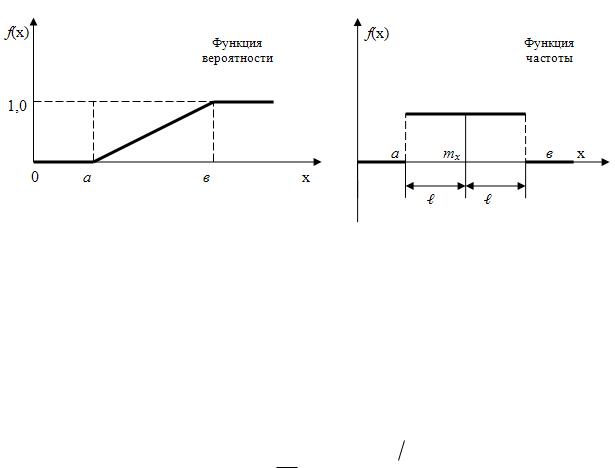
Рис. 2.5. К пояснению правила «трех сигм»

2.5. Закон равной вероятности

Равномерное распределение – такое распределение случайной величины, когда она с одинаковой вероятностью может принимать любое значение в заданных пределах. Такой закон характерен для суммарной погрешности с доминирующим фактором – например, износом инструмента.

Дифференциальный равномерный закон распределения имеет вид:

где a и b – параметры закона, определяющие пределы изменения случайной величины х.

83

Раздел I. Методы и средства управления качеством

____________________________________________________________________

распределения. Первоначально статистический ряд разбивают на k интервалов и подсчитывают число значений случайной величины Х в каждом интервале. В результате получают экспериментальный ряд частот: m 1, m 2 , m 3, , m k . Сле-

дует сразу оговорить, что предпосылкой применения критерия χ2 является достаточная заполненность интервалов частотами. На практике рекомендуется иметь в каждом интервале не менее 5...10 наблюдений. Если число наблюдений в отдельных интервалах мало, имеет смысл объединить эти интервалы. Исходя из предполагаемого теоретического закона распределения вычисляют частоты m, в тех самых интервалах, на которые разбит статистический ряд. В результате получают теоретический ряд частот в k интервалах m1, m2 , m3, , mk . Для про-

верки согласованности теоретического и экспериментального распределения подсчитывают меру расхождения:

и число степеней свободы v. Число степеней свободы равно числу интервалов k минус число ограничений f.

Число ограничений равно числу параметров в рассматриваемом законе распределения, увеличенному на единицу. Например, для Гауссовского закона имеется два параметра: [М(х) и σ]; в этом случае число ограничений равно трем.

Для распределения χ2 составлены специальные таблицы [7]. Пользуясь этими таблицами, можно для каждого значения 2 и числа степеней свободы v определить вероятность Р того, что за счет чисто случайных причин мера расхождения теоретического и экспериментального распределений будет меньше, чем фактически наблюдаемое в данной серии опытов значение χ2. Если эта вероятность Р мала (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе о том, что закон распределения величины Х есть F(x). Эту гипотезу следует отбросить как неправдоподобную. Напротив, если вероятность Р сравнительно велика, можно признать расхождение между теоретическим и экспериментальным распределениями несущественным и отнести его за счет случайных причин. Гипотезу о том, что величина Х распределена по закону F(x), можно считать в этом случае правдоподобной, по крайней мере не противоречащей полученным экспериментальным данным. В таблицах входами являются значение χ2 и число степеней свободы v. Числа, стоящие в таблице, представляют соответствующие значения Р. Насколько должна быть мала вероятность Р для того, чтобы отбросить или пересмотреть гипотезу,— вопрос неопределенный. Он не может быть решен из математических соображений, а должен базироваться на априорных сведениях о физической сущности изучаемого процесса. На практике, если Р < 0,1, рекомендуется проверить эксперимент, если возможно – повторить его. В случае появления повторных расхождений следует попытаться найти наиболее подходящий для описания экспери-

85

Глава 2. Статистические методы контроля и управления качеством продукции

________________________________________________________________________________

ментальных данных закон распределения.

2.7. Пути вероятностного описания совокупности параметров

Ранее было показано, что для вероятностного описания параметров, рассматриваемых в отдельности, можно использовать характеристики m (xi ), (xi ),f (xi ) , где xi – i-й первичный параметр (в случае функции f xi и

его текущие значения).

В конструировании и технологии приборостроения в большинстве случаев приходится иметь дело с совокупностью параметров. Они могут быть независимыми и зависимыми.

Возникает вопрос, как на практике с вероятностной точки зрения описать совокупность параметров,

Наиболее полной характеристикой такого вероятностного описания является многомерная функция плотности распределения f(x-i, ..., Хn.), i = 1 ... n, где n – число параметров рассматриваемой совокупности.

Из теории вероятностей известно, что

n

f x1, , xn f x1 f xn f xi

i 1

Это выражение справедливо для независимых параметров. Поэтому для совокупности независимых параметров можно пользоваться вероятностным описанием этих параметров, рассматриваемых в отдельности, т.е. характери-

стиками m xi , xi ,f xi ,i 1,...,n .

Для зависимых параметров указанное выше выражение несправедливо. Поэтому для вероятностного описания их совокупности следовало было бы

пользоваться многомерной функцией f x1,...,xn` или различными одифика-

циями условных функций.

Однако даже в случае двух параметров (n = 2) мы столкнулись бы со сложностями математического характера, так как f x1, x2 представляет собой поверхность, а условная функция f x1 / x2 – семейство кривых.

Поэтому на практике возникает вопрос, как из многомерных или условных функций извлечь информацию о зависимости параметров в форме, удобной для инженерного использования. Выход может быть найден путем введения такого понятия, как коэффициент корреляции между параметрами (рассмотрен в 3.4).

2.8.Точечные и интервальные оценки параметров

Винженерной практике для различных целей используют точечные и интервальные оценки параметров. Точечной называют такую оценку, которая представляется одним числом, т.е. точкой на числовой оси. Интервальной называют оценку, представленную интервалом значений.

86

Раздел I. Методы и средства управления качеством

____________________________________________________________________

К оценкам предъявляются следующие основные требования:

а) с увеличением числа наблюдений оценка параметра должна приближаться к истинному его значению. Оценку, отвечающую этому свойству называют состоятельной;

б) вычисляя оценку параметра, мы должны быть уверены в том, что заведомо не совершаем ошибку в сторону уменьшения или увеличения оценки, т.е. должны быть уверены в отсутствии систематической ошибки. Оценка, отвечающая этому свойству, называется несмещенной;

в) расхождения между опенками параметра, подсчитанными по результатам n наблюдений, взятых из любого участка теоретически возможного числа наблюдений N, должны быть минимальными. Другими словами, дисперсия оценки должна быть минимальной. Оценку, отвечающую этому свойству, называют эффективной.

Определение точечных оценок математических ожиданий и средних от-

клонений параметров. Пусть произведено n наблюдений параметра х и получены значения x1, x 2 ,...,x n . Определим точечную оценку для математического

ожидания и среднего квадратичного отклонения этого параметра, причем оценки должны отвечать указанным выше требованиям.

Из теории вероятностей известно, что такие оценки могут быть подсчитаны с помощью выражений

Здесь, а при необходимости и далее, оценки будут помечаться, где это важно, где это необходимо подчеркнуть, обозначением параметра или характеристики σ(х)в , m(х)в или XB – выборочная характеристика, или σ(х)г.с., m(х)г.с. –

для генеральной совокупности. Иногда в литературе выборочную σ(х)в обозначают как Sв. Величину (n – 1) в знаменателе формулы (2.21) называют числом степеней свободы.

Определение интервальных оценок параметров. В инженерной практике нередко возникает вопрос о точности и надежности оценки. Для ответа на этот вопрос пользуются такими понятиями, как доверительный интервал и доверительная вероятность.

Под доверительным интервалом понимают диапазон значений, в который с заданной вероятностью попадает истинное значение параметра. Указанную вероятность называют доверительной.

Если мы найдем доверительный интервал, то тем самым укажем интервальную оценку параметра. Покажем, как это делать, на примере математического ожидания параметра.

87

Глава 2. Статистические методы контроля и управления качеством продукции

________________________________________________________________________________

Пусть получена точечная оценка математического ожидания параметра х.

Обозначим эту оценку как M (х).

Доверительный интервал строят обычно симметричным относительно точечной оценки M x , как показано на рис. 2.6.

Рис. 2.6. К определению интервальной оценки

Здесь приняты следующие обозначения:

M – точечная оценка математического ожидания рассматриваемого параметра; для простоты записи знак х опущен;

M – истинное значение математического ожидания; Mн – нижняя граница доверительного интервала; Mв – верхняя граница доверительного интервала;

I – доверительный интервал;

Если мы его найдем, то тем самым укажем интервальную оценку для математического ожидания. Для определения доверительного интервала I, надо знать значение . Для ее нахождения воспользуемся следующим приемом.

Из теории вероятностей известно, что даже при числе наблюдений n, стремящимся к 10–15, закон распределения оценки М*(х) близок к нормальному.

Рис. 2.7. Плотность распределения оценки математического ожидания

88

Раздел I. Методы и средства управления качеством

____________________________________________________________________

0,9973. В инженерной практике могут использоваться и другие значения веро-

1,6; 2 и т.д. – надо отложить влево и вправо от точечной оценки M , чтобы вероятность попадания истинного значения математического ожидания в полученный диапазон была равна вероятности . В общем случае коэффициент t .

определяется как

1

t arg , (2.26)

2

где arg ... – аргумент стандартной функции ... нормального распределе-

89

Глава 2. Статистические методы контроля и управления качеством продукции

________________________________________________________________________________

ния, для которого сама функция Ф*(...) принимает значения, указанные в скобках.

Например, если Ф*(1,64) = 0,95, то arg Ф*(0,95) = 1.64.

В окончательном виде искомый доверительный интервал I , а следова-

тельно интервальная оценка математического ожидания, может быть записана в виде

Пример 2.1. Испытывались на стойкость 2 партии сверл, исходная величина партии 20 штук. К окончанию испытаний (часть сверл были сломаны в процессе испытаний) получены следующие результаты:

Зададимся = 0,95, т.к. не известен закон распределения то с использованием таблиц для критерия Стьюдента, при числе степеней свободы f1 = 14 – 1 = 13 и f2 = 16 - 1 = 15, найдем tкр1 = 2,16; и tкр2 = 2,13.

23 < М(х) = 27 < 31 мин. Аналогично, ∆х2 = 3,9 мин, тогда 11,1 < М(х) <18,9.

2.7. Два способа достижения заданной точности. Выборочный метод

Для обеспечения точности могут быть использованы два способа.

Первый способ – индивидуального получения параметров (разме-

ров), когда оборудование предварительно не настраивается, а заданные параметры Yj обеспечиваются путем постепенного приближения к заданной величине. Заданная точность достигается за счет опыта и квалификации исполнителей, с значительными затратами времени (традиционно, в механической обработке, его называют «способ пробных проходов и промеров»).

Он характеризуется низкой производительностью, высокой себестоимостью. Однако позволяет на неточном оборудовании получать точные детали. Используется в единичном производстве, когда из-за небольшого количества обрабатываемых изделий нецелесообразно производить настройку оборудования, изготавливать специальные приспособления. При сборке изделий аналогом данного метода является регулировка, подгонка, коим присущи те же достоинства и недостатки.

Второй способ - автоматического получения параметров, характеризует-

90