Управление качеством в приборостроении

Раздел I. Методы и средства управления качеством

____________________________________________________________________

1.16.2. Определение коэффициентов влияния

использованием номинальных значений параметров. В случае, если (1.2) имеет сложное аналитическое выражение, нахождение частные производных преобразований и связано с большими затратами времени. Упростить вычисление можно с помощью таблицы[15].

В том случае, если имеется модель функциональной зависимости реальная на ЭВМ определение i можно осуществить с помощью малых отклонений

параметров i . При этом изменяется один из параметров при номинальных

Рис. 1. 18. Линеаризация зависимости Y = f (x)

1.17. Основные положения теории точности и типы погрешностей

Одним из важнейших инженерных принципов, обеспечивающим возможность сборки изделий (в том числе автоматизированной ) без подгонки и регулировки или с минимальным их объемом, возможность ремонта и замены на аналогичные экземпляры без потери качества функционирования – является принцип взаимозаменяемости.

Взаимозаменяемостью – называется принцип нормирования требований к размерам элементов деталей, узлов, механизмов, используемый при конструировании, благодаря которому представляется возможным изготавливать их независимо и собирать или заменять без дополнительной обработки при соблюдении технических требований к изделию.

61

Глава 1. Качество продукции. Предмет и область управления качеством

____________________________________________________________________

Различают геометрическую и физическую взаимозаменяемость, для обеспечения которых нормируют геометрические и физические параметры.

Для обеспечения взаимозаменяемости используют группы стандартов, такие как ЕСКД, ЕСДП – единая система допусков и посадок, которые опираются на международную систему стандартов ICO.

Так для назначения точности линейных и диаметральных размеров элементов деталей в ЕСДП приняты 19 квалитетов точности – 01, 0, 1,2,3,…17. Квалитеты 01,0 и 1 предназначены для концевых мер длины; квалитеты со 2 по 4 для калибров и особо точных изделий. В квалитетах с 5 по 13 даются допуски для сопрягаемых размеров деталей, а в квалитетах с14 по 17 для несопрягаемых.

Стандартизированы также и ИЭТ (изделия электронной техники). Так для резисторов установлено 6 рядов номинальных значений: Е6, Е12, Е24, Е48, Е96, Е192, где цифра после буквы Е указывает число номинальных значений в данном ряде. Нормализованы допускаемые отклонения в процентах в соответствии с рядом: от ±0,001… до ±30.

Отсюда следует, что выпуск продукции соответствующей заданному уровню качества определяется точностью выходных параметров.

Таким образом, точность это степень соответствия полученных параметровзаданным. Различают следующие разновидности:

•заданная точность – с помощью номинального значения параметра и его допустимого отклонения;

•фактическая точность, т.е. реально полученная степень соответствия;

•расчетная точность – т.е. прогнозируемая, основанная на опыте или по-

лученная в результате расчета тем или иным методом.

Для количественной оценки точности используют понятие погрешность, величина которой может быть как абсолютной, так и относительной.

Существует большое количество причин, которые порождают погрешностей различного характера влияющих на отклонения параметров от заданных значений. Разработка системы управления качеством базируется на возможно полном анализе и на рациональной классификации погрешностей – «врагов необходимо знать в лицо».

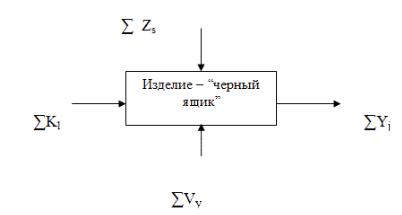
Если рассматривать изделие в виде «черного ящика» (рис. 1.19), то можно предложить следующую классификацию:

•∑Kl – рассеивание конструктивных размеров деталей, входящих в изделие, физических характеристик используемых материалов и комплектующих;

•∑Zs – влияние технологического оборудования и квалификации персонала;

•∑Vy – влияние внешних условий, в том числе источников питания.

Вдальнейшем изложении все входные погрешности объединим под общим обозначением xi.

Врамках системы TQC (Total Quality Control) используют метод 5М, учитывающий факторы, зависящие от человека (man), машины (machine), материала (material), технологического метода (method), измерения (measure).

62

Раздел I. Методы и средства управления качеством

____________________________________________________________________

Рис.1.19. Типы погрешностей

Отдельно следует выделить ошибки методического характера в расчетных формулах используемых при проектировании, ошибки и допущения в экспериментальных данных при физическом или математическом моделировании.

Все перечисленные источники погрешностей в свою очередь можно разделить на следующие группы:

•причины известные, измеряемые, управляемые;

•причины известные, измеряемые, но отсутствует возможность ими управлять;

•причины не известные и, естественно, не управляемые.

Вобщем случае причины разнообразны для разных изделий и предприятий, должны рассматриваться в конкретном анализе; для целей данной работы рассмотрим классификацию погрешностей, возникающих как результат рассмотренных ранее разнообразных причин.

Для целей анализа точности используют следующую классификацию по-

грешностей – систематические (постоянные), закономерно изменяющиеся, случайные.

Систематические (постоянные) ωп – погрешности, постоянные для всех деталей рассматриваемой совокупности, полученные при определенных условиях, например, если при сверлении имеет место смещение оси инструмента (сверла) от заданного положения, то все обработанные детали (полученные отверстия) скопируют имеющуюся погрешность. Как правило, такие погрешности поддаются компенсации.

Закономерно изменяющиеся ωз.и. – погрешности изменяющиеся по какому то (линейному, не линейному ) закону. Обычно это погрешности связанные

сизносами. Так, при автоматическом точении вала не настроенном оборудовании каждая последующая деталь больше предыдущей, из-за износа резца.

Случайные погрешности ωсл. – это погрешности (возникающие не случайно), имеющие при обработке каждой детали случайную величину и случайное направление. Как будет показано ниже, математической характеристикой случайной величины является закон ее распределения. Случайные погрешности можно уменьшать, но компенсировать не возможно.

Вреальности суммарная погрешность является комбинацией перечисленных типов. Совместное влияние перечисленных погрешностей можно оценить

63

Глава 1. Качество продукции. Предмет и область управления качеством

____________________________________________________________________

по формуле:

1.18.Технически достижимая

исреднеэкономическая точность обработки

Винженерной практике часто приходится принимать решения при выборе величины конструкторских или технологических допусков, при выборе методов обработки, когда критерием выбора являются вопросы экономического характера. Рассмотрим эту проблему на примере выбора метода обработки.

Совершенно очевидно, что с повышением требований к точности трудоемкость и стоимость обработки увеличиваются. Это связано с тем, что для уменьшения погрешности необходимо использовать более точные станки и инструменты, снижать режимы резания, уменьшая производительность. Выполнение обработки с высокой степенью точности связано с использованием рабочих высокой квалификации, с повышенной оплатой труда. Сказанное обусловливает следующую зависимость полного (калькуляционного) времени обработки от точности:

где Т0 – постоянная, соответствующая минимально возможной для анализируемого метода обработки затрате времени; ω – суммарная погрешность размеров при обработке деталей по данному методу; А и k – коэффициенты.

Зависимость стоимости обработки С = f (ω ) будет аналогичной.

На рис. 1.20 представлена зависимость Т = f (ω ). Нанесенные пунктиром линии на расстояниям То и ω 0 от осей координат являются асимптотами кривой: То – это время, которое необходимо затратить на обработку детали по данному методу, независимо от требуемой точности , а 0 – это минимально достижимая при данном методе обработки погрешность.

Рис. 1.20. Иллюстрация к теме об экономической точности

64

Раздел I. Методы и средства управления качеством

____________________________________________________________________

На кривой Т = f (ω ) следует различать участки А, В и С. На участке А кривая располагается почти параллельно оси ординат. Значительно увеличивая затраты времени Т и средства С на обработку, можно получить лишь небольшое повышение точности и наоборот. Точность, которая достигается при такой обработке, называют областью технически достижимой точности метода. Работа с допусками ω 0 < δ < ω А протекает неустойчиво, увеличивается вероятность брака: она соответствует случаю, когда для достижения высокой точности используется недостаточно квалифицированный (обоснованный) метод, например, точение для размеров с допусками 7–5 квалитетов точности.

На участке В кривая, наоборот, располагается почти параллельно горизонтальной оси. Здесь при небольшом увеличении Т или С можно значительно повысить точность обработки. Область значений ω > ωБ называют гарантированной точностью метода. Работа с точностью δ > ωБ соответствует случаю, когда какой-либо квалифицированный метод используется в условиях, не требующих высокой точности (например, шлифование при размерах с допусками 13…11 квалитетов. Работа на участке гарантированной точности получается также неэкономичной. В большинстве случаев работают с точностью, соответствующей участку Б кривой, для которого имеет место почти пропорциональная зависимость между Т и ωо. Область ωА…ωБ и будет областью экономической точности рассматриваемого метода. Для определения границ области Б, в которых данный метод является экономически оправданным, необходимо сравнить его с другими методами, которые технически можно применить для выполнения заданной операции.

Теперь можно сформулировать определение экономической точности обработки. Экономической (или средне экономической) точностью какого-либо метода обработки называется точность, обеспечиваемая в нормальных производственных условиях и при затрате времени и средств, не превышающей затрат для других способов, сравниваемых с рассматриваемым. Значения средне экономической точности для наиболее распространенных методов обработки даются в справочниках по технологии приборостроения, они используются при назначении операционных допусков на обработку. Они не остаются неизменными, так как по мере прогресса техники достижение определенной точности становится более экономичным.

1.19. Точность выходных параметров при сборке изделий. Оценка серийнопригодности

На этапе сборки и регулировки из деталей и комплектующих элементов получают готовые изделия. При этом из-за наличия производственного разброса параметров элементов в ряде случаев выходной параметр может выходить за пределы, заданные в ТУ. Свойство конструкции изделия сохранять после сборки и регулировки выходные параметры в допустимых по ТУ пределах называют серийнопригодностью. На практике серийнопригодность описывают процентом выхода годных к эксплуатации устройств после сборки, ко-

65

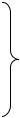
Глава 1. Качество продукции. Предмет и область управления качеством

____________________________________________________________________

торый зависит от суммарной величины погрешностей, сложившихся в каждом изделии случайным образом, т.о. это вероятностная характеристика. Рассмотрим последовательность расчетов, которые могут выполняться при определении серийнопригодности.

В общем случае поле допуска характеризуется верхним отклонением – ВО, нижним – НО координатной середины поля допуска Е. При расчете точности сборки рассматривается поле допуска выходного параметра Yj, которое зависит от полей допусков деталей и узлов, влияющих на данный выходной параметр.

Номинальные размеры связаны уравнением:

Здесь размерная цепь ( где в качестве звеньев могут рассматриваться как геометрические так и физические параметры и размеры) состоит из n звеньев (включая замыкающее), из них m – увеличивающих, а ( n 1) – уменьшающих.

Отметим, что допуск – существенно положительная величина, а его предельные значения, а также координата середины поля допускаскалярные величины. Знак их зависит от положения относительно номинального значения параметра.

Предельные значения замыкающего звена определяются:

Разность предельных значений размеров представляет собой допуски:

Это метод расчета размерных цепей на максимум-минимум обеспечивает 100%-ную взаимозаменяемость при сборке, однако для обеспечения δ∑ часто требуется выполнять при изготовлении очень точные допуски на детали и узлы δi ,что связано с большими экономическими затратами. Формулу (1.32) можно также представить в виде (см. 1.26):

Вероятностный метод. Производственные погрешности, как отмечено ранее, носят случайный характер. Выходные параметры приборов – также случайные величины, поскольку являются неслучайными функциями случайных аргументов – параметров деталей и узлов, характеристик технологического

66

Раздел I. Методы и средства управления качеством

____________________________________________________________________

оборудования. Следовательно, при серийном изготовлении у разных экземпляров технические требования к выходным параметрам будут выполняться в разной степени (с той или иной вероятностью), а расчет размерных цепей должен осуществляться вероятностным методом [27]:

звена;

, i – коэффициент относительной асимметрии распределение

размеров ;

i - коэффициент относительного рассеивания (таб. 1.8);

- коэффициент гарантированной надежности (табл. 1.9).

Таблица 1.9

В расчетах, основанных на применении теории вероятностей, используются числовые характеристики закона распределения случайной величины – среднее квадратичное отклонение σ(х) и математическое ожидание (среднее значение) (х). Однако допуски на детали и сборочные узлы в технической документации указываются с помощью других показателей – половины поля

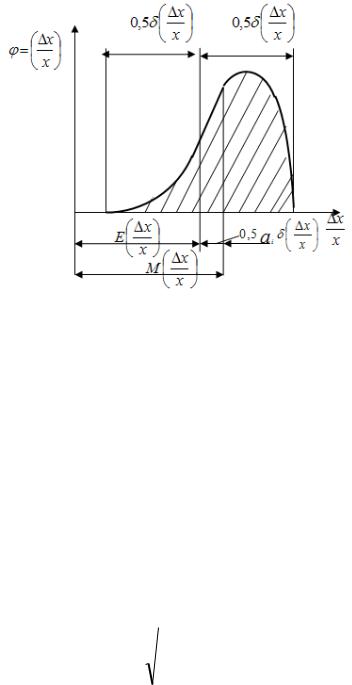
вероятностному методу пользуются числовыми характеристиками законов распределения, связанными с характеристиками поля допуска, как это показано на рис. 1.21. Отсюда, видно, что среднее значение распределения отклонения связано с характеристиками поля допуска следующим образом:

67

Глава 1. Качество продукции. Предмет и область управления качеством

____________________________________________________________________

Рис. 1.21. Характеристики поля допуска и распределения погрешностей

На основании одной из предельных центральных теорем математической статистики обычно принимается допущение, что погрешность выходного параметра, подчиняется нормальному закону распределения (тем быстрее, чем больше звеньев). Тогда (1.22) имеет вид:

С учетом влияния первичных параметров (1.24) перепишем в следующем

виде:

Здесь подразумевается, что погрешности параметров взаимно независи-

мы.

Предельные значения выходного параметра определяются выражением:

Следует отметить, что для количественной оценки процента выхода годных изделий и серийнопригодности в целом, в инженерной практике обычно используют гипотезу о нормальном законе распределения выходного параметра. С учетом этой гипотезы вероятность можно определить по следующей фор-

68

Раздел I. Методы и средства управления качеством

____________________________________________________________________

Если оценка серийнопригодности осуществляется с учетом внешних воздействий (климатических, механических, эксплуатационных), то искомую вероятность можно определить по формуле:

Если такие воздействия вызывают изменения Yj, не подчиняющиеся нормальному закону, то оценка вероятности может осуществляться с помощью неравенства Чебышева:

В тех случаях, когда у прибора проверяется не один, а несколько выходных параметров, оценка серийнопригодности осуществляется по формуле:

Следует отметить, что представленные выше формулы могут быть использованы в различных ситуациях:

•если конструктор определяет вероятное рассеивание на этапе проектирования, то у него отсутствует информация о дисперсии выходного параметра и σ(Y) можно оценить как 1\6 поля допуска;

•если исследователю (технологу) известна реальная точность входных параметров, которая может быть достигнута на данном предприятии, то оценка серийнопригодности может быть получена с учетом такой информации;

•наконец, реальное рассеивание выходного параметра может быть получено путем изготовления опытной партии и определения показателей точности.

1.20.Конструкторско-технологические задачи исследования точности

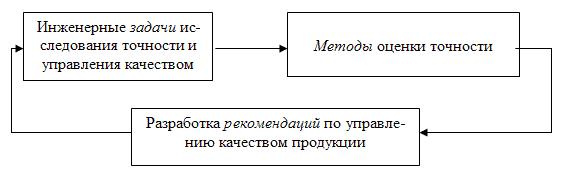
Внастоящее время известны и используются в научных исследованиях и инженерной практике большое количество разнообразных методов оценки точности и управления качеством продукции. В настоящем параграфе будут перечислены с комментариями основные, включенные в рабочую программ по дисциплине. Их использование можно проиллюстрировать следующей схемой – рис. 1.18. Эти методы находятся в сложных взаимодействиях с объектами исследования, могут дублировать друг друга ( что может быть использовано при проверке эффективности методов управления качеством, сходимости моделей с реальной точностью). Один процесс можно описать различными моделями, в то время как одна модель может описывать различные процессы.

69

Глава 1. Качество продукции. Предмет и область управления качеством

____________________________________________________________________

Рис. 1.22. Схема взаимодействия в задачах точности

При проектировании и изготовлении приборов возникают сложные проблемы оптимизации и принятия решений, определяемые функциональным назначением, конструкцией и технологией производства изделий приборостроения, задачами интенсификации их производства и повышения качества. В качестве основного типового метода решения перечисленных задач используют натурные испытания объектов, физическое или математическое моделирование.

В задачах оценки точности и управления качеством чаще используется математическое моделирование на ЭВМ.

Модель – это упрощенная система, отражающая отдельные, наиболее важные стороны явлений изучаемого процесса.

Процесс моделирования должен удовлетворять следующим требованиям:

•эксперимент на модели должен быть проще, оперативнее и экономичнее, чем на объекте;

•должно быть известно правило, по которому можно перенести результаты исследования модели на объект.

Математическое моделирование – это метод количественного и (или) ка-

чественного описания процесса с помощью математической модели, при построении которой реальный процесс или явление описывается с помощью того или иного адекватного математического аппарата.

Все процессы делятся на детерминированные (функциональные ) и стохастические ( вероятностные).

При этом могут возникнуть следующие варианты.

1.Оба признака X и Y тесно связаны друг с другом (например, электрический ток и напряжение в законе Ома). Этот вид связи называют функциональным. Зависимость между обоими признаками выражается в виде формулы. Поэтому при функциональных связях каждому определенному значению х соответствует одно или несколько значений у, и наоборот. Примерами функциональных связей являются все точные законы астрономии, механики, физики и химии.

2.Оба признака X и Y не строго связаны между собой, и связь эта не функциональная, а статистическая. В этом случае каждому фиксированному значению x соответствует ряд изменяющихся вместе с изменением X значений Y и, наоборот, каждому фиксированному значению у соответствует ряд значений X, которые тоже изменяются с изменением Y.

70