Файловый архив студентов. Файловый архив студентов.
1260 вузов, 4603 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Лекции по ОТЭА.pdf
Скачиваний:
58
Добавлен:
13.03.2016
Размер:
2.62 Mб
Скачать
☆
►Содержание►

Ротд = ∫qrпdS

S

Еi = dQdt + Ротд

7. Математические модели дуги.

реальная картина

упрощ¸нная картина

 

Особенности дуги:

1)прямолинейный характер ствола дуги;

2)радиальная зависимость параметров;

3)продольная однородность ствола дуги.

Вышеприведённые особенности должны соблюдаться во всех моделях. Каналовые модели дуги.

d0

Pl Ðè Ðê

12

I – канал дуги; II – теплоотводящий цилиндр Различие моделей:

1)по характеру изменения параметров в первой зоне;

2)по учёту видов переноса теплоты, причём, как правило, используется один вид переноса теплоты;

3)по учёту газодинамических процессов (подобные модели находятся в разработке).

§5. Стационарная дуга в неподвижной среде. Статические вольт-амперные характеристики дуги.

 

2

 

d

 

v

2

 

r

E

 

 

 

 

 

σ = ρ

 

 

 

+ divqV

 

 

h +

2

 

 

 

 

dt

 

 

 

 

 

 

v = 0 ;

T = const

 

 

 

 

 

 

ρ

dh

 

= ρ

d

(CPT )= 0

 

 

 

 

dt

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

qV ≈ qλ

= −λgradT

 

 

 

 

 

 

 

 

 

 

dT

 

 

1 ∂

 

 

dT

divqV

= −div

λ

 

 

 

 

 

= −

 

 

 

 

 

 

Rλ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dR

 

 

R ∂R

dR

 

 

2

 

 

 

1 ∂

 

 

 

 

dT

 

 

 

 

 

E

 

σ +

 

 

 

 

 

Rλ

 

 

 

 

 

= 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R ∂R

 

dR

 

 

 

 

Применение подстановки Кирхгофа. Обобщённая теплопроводность:

T

S = ∫λdT

0

dRdS = dTdS dTdR = λ dTdR

140

 

 

 

 

E

2

σ +

1

 

∂

 

 

 

dS

 

 

= 0

 

 

 

 

 

R ∂R

R

dR

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

 

 

 

 

 

 

 

 

 

 

S1

 

 

 

 

 

 

 

 

 

 

 

S1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T1

 

 

 

 

 

 

 

 

 

 

 

 

T

 

 

 

 

 

 

 

T1

 

T

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

опытная

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

кривая

 

 

 

 

 

 

 

 

 

s*

s1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ò

 

 

 

 

 

 

 

Ò

 

 

 

 

 

 

 

 

S1

S

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Функция σ = f (S ) – примерное отображение кривой σ = f (S ).

 

 

 

 

 

 

 

 

 

 

 

tgα = a2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

σ = a2 (S − S1 )

 

 

 

 

S =

σ

 

+ S

1

;

dS

 

=

 

1

dσ

 

 

 

a2

 

dR

 

a2

dR

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1

∂

 

 

 

 

dσ

 

 

 

E

2

σ

 

 

+

 

 

 

 

 

= 0

 

 

 

 

R a

2

∂R

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dR

 

E

2

σ

 

+

1 1 dσ

 

+

 

 

1

 

d

2σ

 

 

 

R a2

 

dR

 

a2

 

dR2

= 0

 

 

 

 

 

 

 

 

 

 

 

 

 

x = EaR ; dx = EadR ;

 

dx2 = E 2 a2 dR2

1 d 2σ

 

+

 

 

1 dσ

+σ = 0

E 2 a2 dR2

 

 

 

E 2 a2 R dR

 

 

 

 

 

 

d 2σ

 

 

+

1 dσ

+σ

 

 

= 0

 

 

 

 

 

dх2

 

 

х

dх

 

 

 

Уравнение Бесселя:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2 y

+

1 dy

+

 

 

 

 

 

P

 

 

 

 

 

 

dх2

 

 

х dх

1 −

 

x

 

y = 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение в рамке – частный случай уравнения Бесселя при Р = 0.

Решением уравнения являются цилиндрические функции Бесселя.

где J0(x) – функция Бесселя

 

 

 

 

 

 

 

σ = σ0 J0 (x)

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

σ0 – значение электропроводности на оси дуги

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J0 (x)

 

2,405

x

 

х0

= 2,405 = d0

 

141

s

 

 

r

dr

r0 (x0 )

dg = σdV = σ2πrdr

r0

r0

x0

x dx

 

 

 

 

 

(x)=

2πσ0

g = ∫dg = 2π ∫σrdr = 2π ∫

 

 

 

 

 

 

σ

0 J0

 

 

 

 

 

Ea Ea

E

2

a

2

0

0

0

 

 

(0)= 0

 

 

 

 

 

 

 

 

 

 

 

J1

 

 

 

 

 

 

 

 

 

∫J0 (x)xdx = J1 (x)

 

 

 

 

 

 

J1 (2,405)=1,23

 

 

 

 

 

 

 

 

 

 

 

 

g =

 

A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

= gE =

 

A

 

 

 

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

сд

= Еl

 

=

Аlсд

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

сд

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теоретическое представление ВАХ дуги:

x

 

2πσ

 

 

∫0

J0 (x)xdx =

0

J1 (x0 )

2

2

0

 

E a

 

 

uд =U пэ

+ Аlд

uä

 

i

 

 

a

 

 

Uïý

 

 

1

 

 

i1

i2

i

duд

< 0

di

 

 

Реальная связь:

 

Аlд

uд =

 

В зависимости от условий горения:

 

im

 

 

0,3 < m < 3

uä

 

 

элегаз

 

àçîò

 

 

водород

i

142

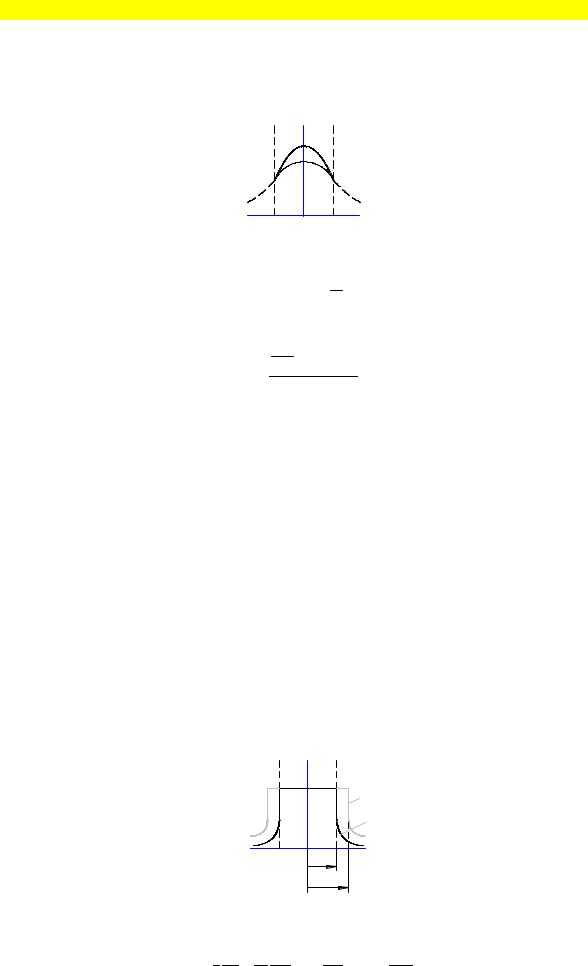
Статические процессы являются начальными процессами.

§6. Модели динамической дуги. Динамические вольт-амперные характеристики дуги.

 

 

 

 

 

 

T = var

 

 

 

 

 

2

 

1

 

∂

∂T

 

 

 

∂T

E

 

σ +

 

 

 

rλ

 

 

 

= ρC

 

 

 

r

 

∂r

P ∂t

 

 

 

 

∂r

 

 

Для решения вышеприведённого уравнения вводят дополнительные упрощения. I. Модель Майра (1943 г.)

Ò

i2 >i1

i2

 

i1

 

r0

r

Дуга не меняет геометрических размеров:

r = r0 = const

Q

g = g0 eQ0 ,

где g0, Q0 – параметры начальных условий

dQdt = Ei − P0

Статический режим:

Ei − P0 = 0

Динамический режим:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ei − P0 ≠ 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Q = Q0 ln

g

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

g0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

di

 

dE

 

 

 

 

 

 

 

 

 

 

 

 

dQ

 

Q0

 

dg

 

 

 

 

 

Q0 E E

 

 

 

 

−i

 

 

 

 

 

 

 

 

 

 

1 di

 

1 dE

=

 

=

dt

 

dt

 

 

= Q

−

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

g dt

 

 

 

i

 

 

 

 

 

 

 

 

 

 

E 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

i dt

 

E dt

 

 

 

 

 

 

 

 

 

 

 

 

 

1 di

 

 

 

 

1 dE

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Q

 

 

 

 

 

 

 

 

 

 

 

−

 

 

 

 

 

 

 

= Ei − P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

0

i dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 di

 

 

 

 

 

1 dE

 

 

 

 

Ei

 

 

 

P0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

 

 

 

 

 

 

 

 

=

 

 

 

−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

dt

 

E

 

dt

 

P

 

Q

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 di

 

 

 

 

1 dE

 

 

 

P

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

 

 

 

 

 

=

 

 

−1

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

i

 

dt

 

 

E

 

dt

 

P

τ

дМ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

где τдМ – постоянная времени дуги II. Модель Касси

 

 

 

 

 

Ò

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i2

 

 

 

 

 

 

 

 

 

 

i1

 

 

 

 

 

 

 

r01

 

r

 

 

 

 

 

 

 

r02

 

 

 

 

 

 

Т = const

 

 

 

 

 

 

 

r0

= var

 

 

 

1 di

 

1

dE

 

 

E

2

 

1

 

 

 

 

 

i dt

−

E dt

 

=

 

E0

 

−1

τдK

 

 

 

 

 

 

 

 

 

 

 

143

 

 

 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности