K dW

dS

dS'

dS

dS′ = dS cos Θ

Телесный угол:

dΩ = drS2 ′

ϕмК = 4πμр 0 ∫S dΩ

ϕмК = 4πμр 0 ΩsK

Для однослойной катушки:

p = wк μ0i ,

где wк – число витков катушки

§3. Квазипотенциальные магнитные поля.

rotH = j

H = Hv + H p ,

где Hrv – вихревая составляющая напряжённости магнитного поля;

H p – квазипотенциальная составляющая напряжённости магнитного поля

rotHv = j

Для вихревого магнитного поля:

divB = div(μHv + μH p )= 0

Принимается, что:

μ ≈ const

div(μH p )= −div(μHv )= −μdivHv = ρм

ρ

2ϕм = − μм

Для определения локального заряда ρм задаются значением Hv , которое должно удовлетворять уравнению:

87

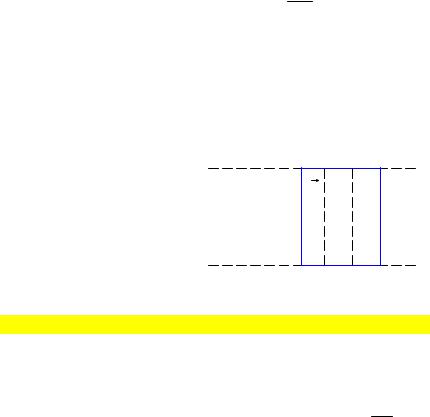
rotHv = j

Для вышеприведенного уравнения можно определить частное решение, в то время как для уравнения rotH = j требуется полное решение.

J = J x i + J y j + J z k Hv = Hvx i + Hvy j + 0

rotz Hrv = ∫dJdzz dz = ∫dJ z = J z

Последовательность метода:

1)выбирается значение Hrv ;

2)определяется локальный заряд ρм:

ρм = −div(μHv )

Варианты размещения зарядов:

1

J

23

Нужно стремиться сократить область зарядов в районе ΙΙΙ. В ряде случаев вводятся фиктивные токи.

§4. Метод сеток для расчёта потенциальных магнитных полей.

Метод сеток – это численный метод решения дифференциальных уравнений Лапласа и Пуассона для скалярного магнитного потенциала.

ρм = f (x; y; z)

ρ

2ϕм = 0 ; 2ϕм = − μм

Каждая реальная задача представляет собой совокупность областей.

88

m0

Ã12 m2

m1

Ã23

Ã13

m3

Ряд величин остаются постоянными, а ряд делают скачки.

Вn1 = Bn2 Г12

Hτ1 = Hτ 2 Г12

Для каждой области составляется группа уравнений, рассматриваются граничные уравнения, а

затем решается вся группа уравнений.

V → ∞

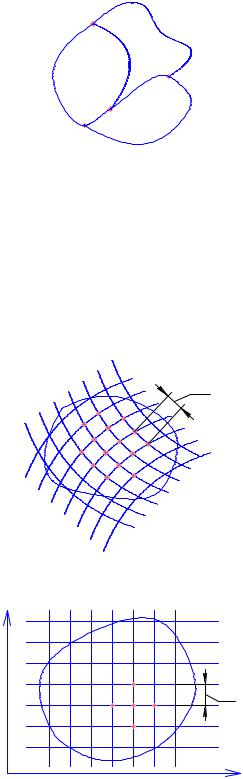
Реально решение задачи сводится к определению скалярного магнитного потенциала для рассматриваемого конечного числа точек N. В качестве искомых точек принимаются узлы сеток, которые разбивают область решения на подобласти.

Для плоскостных задач в качестве подобластей принимаются треугольники, квадраты и т.д. Чем меньше ячейка, тем больше узлов и тем больше чисел.

h

Условия разделения области на сетки:

1)достаточная точность – шаг сетки h должен быть приемлемым;

2)линии сеток должны совпадать с границами разделения разных областей.

89

ϕ1 +ϕ2 +ϕ3 +ϕ4 = 4ϕ0

Должно быть не меньше сотни узлов.

Для каждого узла составляется своё уравнение.

Система алгебраических уравнений, в которой число уравнений и неизвестных зависит от числа узлов N:

а11ϕ1 + а12ϕ2 +... = b11 , а21ϕ1 + а22ϕ2 +... = b22 ,

...

аN1ϕ1 + аN 2ϕ2 +... = bNN

Сложность системы уравнений зависит от того, как пронумерованы узлы. Если хорошо пронумеровать узлы, то можно получить диагональную матрицу. В любом случае получается малозаполненная матрица.

Метод сеток может быть применён при решении задач теории поля на вычислительной технике. Математическое отступление 1.

1. Понятие функционала.

Функция – это связь определённой величины с совокупностью независимых переменных. x → y = f (x)

x → v = f (x)→ y – сложная функция

Функционал – это числовая функция, определённая на множестве независимых функций.

F(ϕj )= ∫b ϕ j (x)dx ,

2. Понятие вариационной задачи (расширение понятия экстремума функции и его определения). Вариационная задача – это задача нахождения функции, при которой функционал имеет макси-

мальное значение. Порядок действий: 1)

∂∂Fϕ = 0 ;

2) φj - ?

§5. Основные положения расчёта магнитных полей методом конечных элементов.

Метод конечных элементов состоит в решении вариационной задачи для функционала от пробных функций, эквивалентирующих скалярный магнитный потенциал.

Энергия магнитного поля:

Wм = V∫ BH2 dV B = μH ; μ = const

Wм = μ2 V∫H 2 dV

H = −gradϕм = − ϕм

90

Wм = μ2 V∫ 2ϕмdV

ρ

2ϕм = − μм

Вышеприведённые соотношения справедливы для потенциального поля. Функционал от пробной функции:

F(u)= μ ∫( u)2 dV , 2 V

где u(x; y; z) – пробная функция

∂F = 0 ∂u j

При каких-то функциях функционал F(u) может быть эквивалентен формуле для энергии. Теорема. Экстремум функционала F(u) будет соответствовать энергии, при некоторой функции

u j = ϕм .

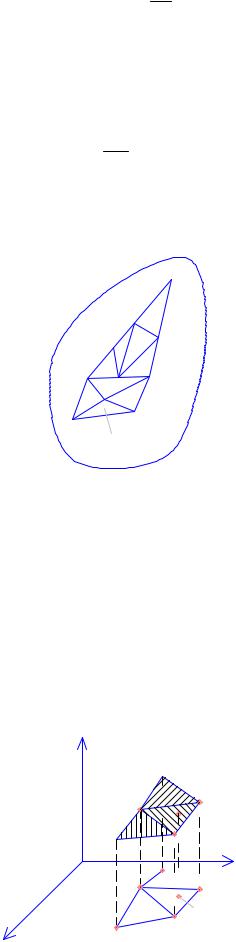
Область решения в методе конечных элементов разделяется на подобласти (конечные элементы):

подобласть

Вся область будет представлять область отдельных элементов определённого типа, например, в виде множества треугольников.

Особенности метода конечных элементов:

1)нет необходимости учитывать границы раздела;

2)число элементов должно быть конечным;

3)размеры элементов не одинаковы и они должны быть тем меньше, чем выше интенсивность поля. В том месте, где наибольшее значение магнитной индукции, должны быть наименьшие элементы и наоборот.

4)однотипность пробной функции в каждом элементе.

Простейший тип пробной функции – полиномиальная функция. Обычно достаточно полинома первого порядка.

u(x; y)= a0 + a1 x + a2 y

Пробные функции отличаются лишь набором чисел {а0 ; а1 ; а2 ;...}. u

u1 u3

u2

x

1 {x1 ;y1 } 5 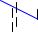3 {x3 ;y3 }

91

u1 = a0 + a1 x1 + a2 y1 , u2 = a0 + a1 x2 + a2 y2 , u3 = a0 + a1 x3 + a2 y3 a0 = (хj ; y j ;u j )

a1 = ...

a2 = ...

u(x; y)=α1 (x; y)u1 +α2 (x; y)u2 +α3 (x; y)u3

Каждая пробная функция есть функция значений узловых потенциалов.

В зоне стыка элементов (во всей области решения задач) обеспечивается непрерывность пробных функций.

α1 (x; y)= b0 + b1 x + b2 y ,

α2 (x; y)= c0 + c1 x + c2 y ,

α3 (x; y)= d0 + d1 x + d2 y

N

F = ∑F (l ) = ∑ul ,

l =0

где N – число узлов

∂F = 2B1u1 + u2C1 + u3C2 = 0

∂u1

В итоге можно получить слабо заполненную матрицу, причём порядок полученной системы уравнений может быть ниже, чем в методе сеток.

На практике для получения остроты экстремума используется упрощённая форма функционала. Математическое отступление 2.

Интегральное уравнение.

R L

U0 +

- C

U0 = ir + jωL = i(r + jxL )

ir + L di + 1 ∫t idt = 0 dt C 0

92

Интегральным уравнением называется функциональное уравнение, включающее интегральное преобразование над неизвестной функцией.

β(х)f (x)−λ∫K(x;t)f (t)dt = F(x),

V

где К(x;t) – ядро интегрального преобразования; λ – собственное число

Применение преобразования Лапласа:

Два типа интегральных уравнений:

1)уравнение Фредгольма – применение определённого интеграла;

2)уравнение Вольтера – применение неопределённого интеграла.

§6. Основные положения метода вторичных источников (метода интегральных уравнений) в решении задач магнитных полей.

Метод вторичных источников подразумевает решение интегрального уравнения для источников поля в немагнитной среде с переходом к векторам поля на базе фундаментальных решений.

divB = 0

B = μ0 μr H

Br = div(μ0 μr Hr)= μ0 (μr H )= μ0 (μr H + H μr )= μ0 μr divHv + μ0 Hvdivμr = 0 μr divH = −Hdivμr

где ρм – фиктивные магнитные заряды Численное значение фиктивных магнитных зарядов в методе вторичных источников отличается

от значений зарядов в предыдущих методах.

Возможно использование фундаментальных уравнений для немагнитной среды. Фундаментальное решение для точечных зарядов:

В некоторых задачах кроме фиктивных магнитных зарядов вводят фиктивные объёмные плотности заряда σф и фиктивные токи jф. Таким образом, количество преобразований увеличивается и получается система интегральных уравнений.

Вектора определяются по соотношениям для фундаментальных решений. Интеграл можно определить методом Симпсона.

Расчёт ведётся только по объёму рассматриваемого тела.

93