Глава 5

Одномерная случайная величина

Случайная величина - третье фундаментальное понятие теории вероятностей после понятий "случайное событие"и "вероятность". Случайные величины могут быть одномерными и многомерными. В настоящей главе рассматриваются одномерные случайные величины, которые в пределах главы будут называться просто случайными величинами.

5.1Определение случайной величины

Определение. Случайной величиной X называется числовая функция, определенная на пространстве элементарных событий Ω, которая каждому элементарному событию ω ставит в соответствие некоторое число.

При этом предполагаются определенными вероятности событий X < x для любых вещественных чисел x.

Таким образом, случайная величина - это вещественная переменная X, значения которой определяются исходами эксперимента E. Значения случайной величины - случайные числа. Случайные величины обычно обозначаются последними буквами латинского алфавита X, Y, Z.

Примеры случайных величин:

1.Число выпавших очков при бросании игральной кости.

2.Число бракованных изделий партии.

3.Время работы прибора до первого отказа.

4.Результат измерения.

Вотличие от детерминированного подхода, устанавливающего жесткую функциональную связь между аргументом и функцией, для случайной величины можно априорно указать лишь вероятности попадания значения случайной величины в некоторое числовое множество, например, X < x, a ≤ X ≤ b, X = a и т.д.

Законом распределения случайной величины называется любое правило, указывающее вероятности отдельных значений случайной величины или множества этих значений.

Таким исчерпывающим законом случайной величины является ее функция распределения, обозначаемая F (x) или FX (x).

28

Функцией распределения случайной величины X называется функция FX (x), которая для любого вещественного числа x равна вероятности события X < x.

Таким образом, по определению

FX (x) = P (X < x).

Справедливы следующие свойства функции распределения:

1.F (−∞) = 0, так как F (−∞) = P (X < −∞) = P ( ) = 0.

2.F (+∞) = 1, так как F (+∞) = P (X < +∞) = P (I) = 1.

3.F (x) - неубывающая функция.

4.F (x) непрерывна слева в любой точке x: F (x − 0) = F (x).

5.P (a ≤ X ≤ b) = F (b) − F (a).

Замечание. Первые 4 свойства функции распределения являются характеристическими. Это означает, что всякая функция F (x), обладающая первыми четырьмя свойствами, может быть функцией распределения некоторой случайной величины X.

Будем различать дискретные и непрерывные случайные величины.

5.2 Дискретная случайная величина

Определение. Случайная величина называется дискретной, иначе - дискретного типа, если множество ее значений может быть занумеровано натуральными числами (т.е. оно конечное или счетное).

Закон распределения дискретной случайной величины удобно задать с помощью формулы

pk = P (X = xk), k = 1, 2, . . . ,

которая определяет вероятности принятия случайной величиной ее отдельных значений xk.

Последовательность пар (x1, p1), (x2, p2), ... образует так называемый ряд распределения.

В случае конечного числа значений ряд распределения удобно оформить в виде таблицы распределения:

Таблицу распределения наглядно можно представить в виде полигона (многоугольника) распределения. Для этого точки (xk, pk) плоскости xOy соединяются отрезками (рис.5.1).

Заметим, что

n

X

pk = 1,

k=1

так как события X = xk, k = 1, . . . , n попарно несовместны и образуют полную группу.

29

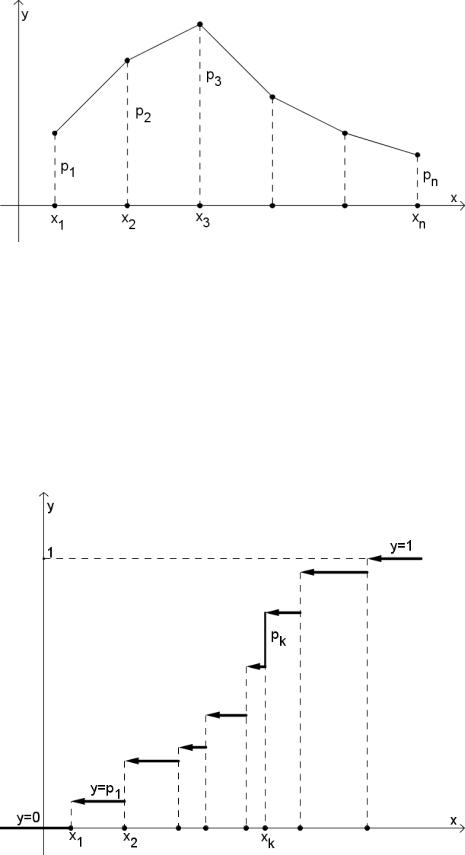
Рис. 5.1: Полигон распределения

Функция распределения дискретной случайной величины имеет вид

X

F (x) = pk.

xk<x

Здесь суммирование ведется по всем k, для которых xk < x.

Функция распределения F (x) есть сумма вероятностей тех точек, которые расположены левее точки x.

Графиком функции распределения является ступенчатая линия со скачками pk в точках

xk.

Рис. 5.2: График функции распределения дискретной случайной величины

30