Дополнительная область V \Vk называется областью допустимых значений статистики критерия. Если Z (V \Vk), то гипотеза H0 при заданном уровне значимости α принимается. Обычно говорят более осторожно: H0 не противоречит имеющейся выборке, т.е. гипотеза H0 правдоподобна.

Область Vk можно выбрать неоднозначно. Однако, зная закон распределения случайной величины Z, хотя бы асимптотический, т.е. при большом объеме выборки n, и, налагая на Vk дополнительные условия, можно критическую область найти однозначно, задав величину α.

Общая схема проверки статистических гипотез

1.Выдвигаются проверяемая и альтернативная гипотезы H0, Ha.

2.Выбирается уровень значимости α (обычно 0,001; 0,01; 0,05; 0,1).

3.Выбирается статистика Z критерия значимости и соответствующая ей, уровню значимости и проверяемым гипотезам H0 и Ha критическая область Vk, являющаяся частью

области V значений статистики Z. При этом V \Vk будет областью допустимых значений

Z.

4.Вычисляется выборочное значение ZB статистики Z.

5.Формулируется критерий проверки. Если ZB Vk, то гипотеза H0 отвергается, так как в результате одного лишь испытания, получения выборки произошло практически невозможное событие ZB Vk с вероятностью α. Если ZB (V \Vk), то гипотеза H0 принимается.

Определение. Критерием согласия называется критерий значимости, применяемый для проверки гипотезы о генеральном законе распределения.

Заметим, что существуют и другие схемы проверки статистических гипотез.

12.3Ошибки первого и второго рода. Односторонний и двусторонний критерий

12.3.1 Ошибки первого и второго рода

Суждения о принятии или отвержении выдвинутой статистической гипотезы не являются абсолютными, а носят лишь вероятностный характер, т.е. являются правдоподобными. Принимая или отвергая гипотезу, мы можем совершить ошибку.

Определение. Ошибкой первого рода называется ошибка отвержения правильной гипотезы.

Определение. Ошибкой второго рода называется ошибка принятия основной гипотезы при условии того, что верной является альтернативная гипотеза.

Вероятность ошибки первого рода равна уровню значимости, т.е.

α = P (Z Vk/H0).

Эта формула означает, что гипотеза H0 отвергается с вероятностью α, хотя эта гипотеза верна.

Вероятность ошибки второго рода обозначается β:

β = P (Z V \Vk/Ha).

Эта формула означает, что принимается гипотеза H0 с вероятностью β, хотя верна альтернативная гипотеза Ha.

83

При той схеме проверки гипотез, которая сформулирована выше, вероятность α задается. Вероятность же β приходится находить. Это делается в редких случаях, так как для этого нужно знать распределение статистики Z для случая альтернативной гипотезы Ha.

Принципы назначения уровня значимости α при проверке статистической гипотезы согласуются с опасностью совершения ошибок первого и второго рода. Эти принципы вообще находятся вне статистики. Они выдвигаются практикой.

Для того, чтобы проверяемая гипотеза была достаточно обоснованно отвергнута, уровень значимости выбирают достаточно малым; в практике: 0,01; 0,001. Напротив, если делается вывод о принятии гипотезы, то уровень значимости не должен быть очень малым, ибо в этом случае расширяется область допустимых значений V \Vk, и даже при неверной гипотезе статистика Z критерия может попасть в эту область за счет случайных колебаний. Будет совершена ошибка второго рода. Уровень значимости в этом случае можно взять равным 0,05; 0,10. Чем меньше уровень значимости, тем меньше вероятность забраковать верную гипотезу, т.е. совершить ошибку первого рода, но при этом увеличивается вероятность принятия неверной гипотезы, т.е. совершения ошибки второго рода.

12.3.2 Односторонний и двусторонний критерии

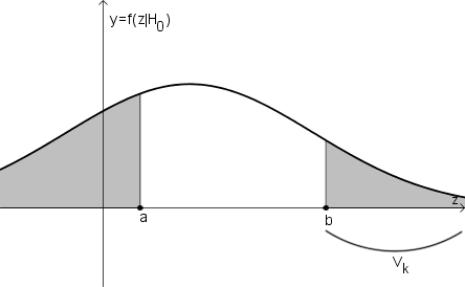
Пусть известен закон распределения статистики критерия Z (хотя бы асимптотический). Будем предполагать, что известна плотность вероятности f(z|H0) при условии, что справедлива проверяемая гипотеза H0. График плотности изображен на рисунке.

Рис. 12.1: Правосторонняя критическая область

Пусть для простоты область значений Z - вся вещественная ось.

Если критическая область Vk представляет собой промежуток (−∞, a) или (b, +∞), то соответствующий критерий называется односторонним (левосторонним или правосторонним).

Если же критическая область является объединением этих полубесконечных промежутков: Vk = (−∞, a) (b, +∞), то соответствующий критерий называется двусторонним.

84