
- •МАТЕМАТИКА
- •ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
- •ВВЕДЕНИЕ
- •Раздел. I. ЛИНЕЙНАЯ АЛГЕБРА
- •Тема 1. Линейная алгебра
- •1.1. Вычисление определителей
- •1.1.1. Типовые примеры
- •1.1.2. Контрольные вопросы
- •1.1.3. Практические задания
- •1.2. Действия над матрицами
- •1.2.1. Типовые примеры
- •1.2.2. Контрольные вопросы
- •1.2.3. Практические задания
- •1.3. Решение систем линейных алгебраических уравнений.
- •1.3.1. Типовые примеры
- •1.3.2. Контрольные вопросы
- •1.3.3. Практические задания
- •Тема 2. Векторная алгебра
- •2.1. Векторы. Линейные операции над векторами.
- •2.1.1. Типовые примеры
- •2.1.2. Контрольные вопросы
- •2.1.3. Практические задания
- •2.2. Произведения векторов
- •2.2.1. Типовые примеры
- •2.2.2. Контрольные вопросы
- •2.2.3. Практические задания
- •2.3. Комплексные числа
- •2.3.1. Типовые примеры
- •2.3.2. Контрольные вопросы
- •2.3.3. Практические задания
- •Тема 3. Аналитическая геометрия
- •3.1. Основные задачи аналитической геометрии
- •3.1.1. Типовые примеры
- •3.1.2. Контрольные вопросы
- •3.1.3. Практические задания
- •3.2. Кривые второго порядка
- •3.2.1. Типовые примеры
- •3.2.2. Контрольные вопросы
- •3.2.3. Практические задания
- •Раздел. II. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •Тема 4. Предел функции
- •4.1. Элементы теории множеств. Понятие функции
- •4.1.1. Типовые примеры
- •4.1.2. Контрольные вопросы
- •4.1.3. Практические задания
- •4.2. Теория пределов
- •4.2.1. Типовые примеры
- •4.2.2. Контрольные вопросы
- •4.2.3. Практические задания
- •4.3. Предел и непрерывность функции
- •4.3.1. Типовые примеры
- •4.3.2. Контрольные вопросы
- •4.3.3. Практические задания
- •Тема 5. Дифференциальное исчисление
- •5.1. Вычисление производных
- •5.1.1. Типовые примеры
- •5.1.2. Контрольные вопросы
- •5.1.3. Практические задания
- •5.2. Исследование функций на экстремумы и интервалы монотонности
- •5.2.1. Типовые примеры
- •5.2.2. Контрольные вопросы
- •5.2.3. Практические задания
- •5.3. Исследование функций двух переменных
- •5.3.1. Типовые примеры
- •5.3.2. Контрольные вопросы
- •5.3.3. Практические задания
- •Тема 6. Интегральное исчисление
- •6.1. Решение задач на нахождение неопределенных интегралов. Нахождение неопределенных интегралов различными методами
- •6.1.1. Типовые примеры
- •6.1.2. Контрольные вопросы
- •6.1.3. Практические задания
- •6.2. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов
- •6.2.1. Типовые примеры
- •6.2.2. Контрольные вопросы
- •6.2.3. Практические задания
- •7.1. Сходимость знакоположительных рядов
- •7.1.1. Типовые примеры
- •7.1.2. Контрольные вопросы
- •7.1.3. Практические задания
- •7.2. Исследование сходимости знакочередующихся рядов
- •7.2.1. Типовые примеры
- •7.2.2. Контрольные вопросы
- •7.2.3. Практические задания
- •Тема 8. Функциональные ряды
- •8.1. Нахождение интервала и радиуса сходимости степенных рядов
- •8.1.1. Типовые примеры
- •8.1.2. Контрольные вопросы
- •8.1.3. Практические задания
- •Раздел. IV. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- •Тема 9. Численные методы
- •9.1. Нахождение корней уравнений итерационным методом
- •9.1.1. Типовые примеры
- •9.1.2. Контрольные вопросы
- •9.1.3. Практические задания
- •9.2. Примеры численного интегрирования
- •9.2.1. Типовые примеры
- •9.2.2. Контрольные вопросы
- •9.2.3. Практические задания
- •9.3. Примеры численного интерполирования
- •9.3.1. Типовые примеры
- •9.3.2. Контрольные вопросы
- •9.3.3. Практические задания
- •Раздел. V. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- •Тема 10. Случайные события
- •10.1. Задачи на вычисление классической вероятности и относительной частоты
- •10.1.1. Типовые примеры
- •10.1.2. Контрольные вопросы
- •10.1.3. Практические задания
- •Тема 11. Случайные величины
- •11.1. Законы распределения случайной величины
- •11.1.1. Типовые примеры
- •11.1.2. Контрольные вопросы
- •11.1.3. Практические задания
- •Тема 12. Математическая статистика
- •12.1. Методы математической статистики
- •12.1.1. Типовые примеры
- •12.1.2. Контрольные вопросы
- •12.1.3. Практические задания
- •РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

2.1.7. Найти координаты центра тяжести однородного стержня с концами
A(−2,1,4), B(0,5,−2) .
2.2. Произведения векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.2.1. Типовые примеры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 2.2.1. Для двух |
|
|
|
|
|
|
|
a и |
|
b |
|
|
b |
|
|||||||||||||||
|
|
|
векторов |
|
дано |
a |
= 4 , |
= 5 , |
|||||||||||||||||||||
α = (a, b) = π. Найти a b , a2 , |
(a + 2b)(a − b). |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По определению скалярного произведения векторов имеем |
|||||||||||||||||||||||||||||
ab = |
|
a |
|
|
|
b |
|
|
|
cos(a b ) = |
4 5 cos |
|
π |
=10 , |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a2 = |
|
a |
|
|
|
a |
|
cos(0 |
) = |
|
a |
|
2 =16 . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Используя свойства скалярного произведения, получим
(a + 2b )(a − b )= a2 + 2b a − a b − 2b 2 = a2 + a b − 2b 2 = = a 2 + a
 b cos(a b) − 2 b 2 =16 +10 − 2 25 = −24.
b cos(a b) − 2 b 2 =16 +10 − 2 25 = −24.
Пример 2.2.2. Дано: a = (0,−1,1), b = (2,1,0).
Найти: 1) a b ;
2) (3a − b )(a + b ) двумя способами.
Решение. 1) Используя формулу для вычисления скалярного произведения, получим
ab = 0 2 + (−1) 1 +1 0 = −1.
2) первый способ: раскроем скобки, пользуясь свойствами скалярного произведения,
(3a − b )(a + b )= 3a2 − b a + 3ab − b 2 = 3a2 + 2ab − b 2 .
Так как ab = −1, 3a2 = 3 a 2 = 3 (0 +1 +1)= 6 b 2 = 4 +1 + 0 = 5 , то получим
(3a − b )(a + b )= 6 − 2 − 5 = −1;
3)второй способ: найдем координаты сомножителей
18
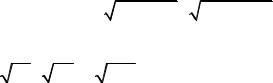
3a − b = (0,−3,3) − (2,1,0) = (−2,−4,3),
a + b = (0,−1,1)+ (2,1,0)= (2,0,1).
Тогда
(3a − b )(a + b )= (−2) 2 + (−4) 0 + 3 1 = −1.
Пример 2.2.3. Даны вершины треугольника A(−1,0,2), B(0,3,−1),
C (4,2,1). Найти угол при вершине А.
Решение. Составим два вектораAB и AC с общим началом – точкой А. Получим
AB = (0 +1,3 − 0,−1 − 2) = (1,3,−3),
AC = (4 +1,2 − 0,1 − 2) = (5,2,−1).
Найдем косинус угла А, как косинус угла между векторами AB и AC
|
|
|
|
AB AC |
|
|
|
1 5 + 3 2 + (−3) (−1) |
|
|
|||||||||||||||||||||||||||||||
cos( AB AC) = |
|
|
|
= |
|
= |
|||||||||||||||||||||||||||||||||||
|
|
|
AB |
|
|
|
AC |
|
1 + 9 + 9 25 + 4 +1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
14 |
|
|
|
= |
|
14 |
|
≈ 0,59. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
19 |
30 |
|
570 |
|
|
|
|||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
A = arccos0,59 ≈ 540. |
|
|
|
|
|||||||||||||||||||||||||||||
Пример 2.2.4. Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
(a + b)×(b − 2a) |
|
, если |
|
||||||||||||||||||||||||
|
|
|
a ×b |
|
, |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
a |
|
= 2, |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
= 4, α = a b = |
6 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. В силу определения векторного произведения имеем |
|||||||||||||||||||||||||||||||||||||||||
|
a ×b |
|
= |
|
a |
|
|
|
b |
|
|
|
|
|
= 2 |
4 |
1 |
= 4. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
sin a |
|
b |
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пользуясь свойствами векторного произведения, получим |
|
||||||||||||||||||||||||||||||||||||||||
(a + b)×(b − 2a)= a ×b + b ×b − 2a × a − 2b × a. |
|
||||||||||||||||||||||||||||||||||||||||
Так как a × a = 0, b ×b = 0, b × a = −a ×b, |
то |
(a + b)×(b − 2a)= 3 a ×b, а |
|||||||||||||||||||||||||||||||||||||||
значит
19

(a + b)×(b − 2a) = 3 4 =12.
Пример 2.2.5. Дано: a = (−1,3,0,), b = (0,2,−1).
Найти a ×b , a ×b , (a − 2b)×(2a + 3b).
Решение. Пользуясь формулой векторного произведения, получим
|
|
|
|
|
|
3 |
0 |
|
, − |
|
−1 |
0 |
|
, |
|
−1 3 |
|
|
= (−3, |
−1, |
−2), |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
a ×b = |
|
2 |
−1 |
|
|
0 |
−1 |
|
|
0 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
тогда |
|
a ×b |
|
= (−3)2 + (−1)2 + (−2)2 = |
14 ≈ 3,74 . |
|
|
||||||||||||||
|
|
|
|
||||||||||||||||||
Найдем координаты сомножителей
a − 2b = (−1,3,0) − (0,4,−2)= (−1,−1,2),
2a + 3b = (−2,6,0) + (0,6,−3)= (−2,12,−3).
Получим
|
|
|
|
−1 2 |
|
, |
|
|
− |
|
−1 2 |
|
, |
|
|
|
|
−1 −1 |
|
|
−7,−14). |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
(a − 2b )×(2a + 3b )= |
|
12 |
−3 |
|
|
|
−2 |
|
−3 |
|
|
|
|
−2 12 |
|
= (−21, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример 2.2.6. Найти площадь треугольника АВС, если известны его вер- |
|||||||||||||||||||||||||||||||||
шины A(1,−1,2), B(2,−3,5), C (3,−1,3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. Воспользуемся формулой площади треугольника через коорди- |
|||||||||||||||||||||||||||||||||
наты векторов AB, AC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
S |
= |
1 |
|
|
AB × AC |
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
AB = (1,−2,3), AC = (2,0,1) и их |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для этого найдем координаты векторов |
|
|
|
|
|||||||||||||||||||||||||||||
векторное произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−2 3 |
|
,− |
|
1 3 |
|
, |
|
1 −2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
AB × AC = |
|
|
0 |
1 |
|
|
2 1 |
|
|
2 |
0 |
|
|
|
|
= (−2, 5, 4). |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
AB × AC |
|
= |
4 + 25 +16 = |
|
|
|
|
|
|
45 ≈ 6,7, |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то площадь треугольника равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
20
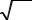
S = |
1 |
45 ≈ 3,35 (кв.ед). |
|
2 |
|
Пример 2.2.7. Найти вектор N, перпендикулярный плоскости, в которой лежат три точки A(1,−1,0), B(0,1,2), C (2,0,1).
Решение. Если вектор N перпендикулярен плоскости, то он перпендику-
лярен любым прямым, лежащим на плоскости, в частности, векторам AB и AC .
Это значит, что в качестве вектора N можно взять векторное произведение
AB × AC . Так как, AB = (−1,2,2), AC = (1,1,1), |
|
то |
|
|
|
|
|||||||||||||
|
|
2 2 |
|
, − |
|
−1 2 |
|
, |
|
−1 2 |
|
|
−3). |
||||||
|
|
|
|
|
|
||||||||||||||
N = AB × AC = |
|
|
1 1 |
|
|
1 |
1 |
|
|
1 |
1 |
|
= (0,3, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2.2.8. Найти смешанное произведение трех векторов |
|||||||||||||||||||
a = (0,1,−1), b = (2,0,−1), c = (−1,2,1). |
|
||||||||||||||||||
Решение. Найдем смешанное произведение векторов |
|
||||||||||||||||||
abc = |
|
0 1 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 0 −1 |
|
=1 − 4 − 2 = −5. |
|
||||||||||||||||
|
−1 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.2.2. Контрольные вопросы
1)Что называется скалярным произведением двух векторов?
2)Сформулируйте свойства скалярного произведения.
3)Запишите выражение скалярного произведения в координатах.
4)Как найти угол между векторами?
5)Запишите условие перпендикулярности двух векторов.
6)Какая тройка векторов называется правой?
7)Что называется векторным произведением двух векторов?
8)Перечислите свойства векторного произведения.
9)Запишите формулу для вычисления векторного произведения в координатах.
10)Запишите формулы для вычисления площадей треугольника и параллелограмма по известным координатам их вершин;
11)Что называется смешанным произведением векторов?
12)Как записывается смешанное произведение в координатах?
13)Как найти объем параллелепипеда и пирамиды по их вершинам?
14)Какие векторы называются компланарными?
15)Каково условие компланарности векторов?
21
