Среди изделий первого завода 70% первосортных, второго завода – 80 %, третьего завода – 90 %. Куплено одно изделие.
1)Найти вероятность того, что оно первосортное.
2)Изделие оказалось первосортным. Найти вероятность того, что купленное изделие выпущено первым заводом.
Тема 11. Случайные величины
11.1.Законы распределения случайной величины
11.1.1.Типовые примеры
Пример 11.1.1.
Дискретная сл. в. X задана рядом распределения
|
|
|
|
ТАБЛИЦА 11.1.1 |
|
|
|
|
5 |
|
|
X |
1 |
2 |
7 |
||
|
|
|
0,5 |
|
|
P{X = xk } |
0,06 |
0,25 |
|
0,19 |
|
|
|
|
|
|
|
Требуется:
1)построить многоугольник распределения;
2)найти функцию распределения F(x) и построить ее график;
3)найти mx , Dx , σx ;
4)найти P{2 ≤ X ≤ 7}.
Решение.
1) построим многоугольник распределения (рис. 11.1.1)
р
0,5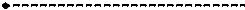 
0,25
0,19
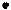
0,06
0 |
1 |
2 |
5 |
7 |
x |
РИС. 11.1.1
104
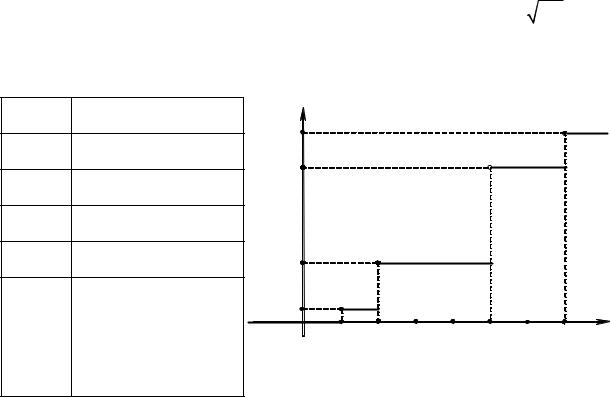
2) Функцию F(x) найдем в виде таблицы и построим ее график (Рис.
11.1.2).
3) mx =1 0,06 + 2 0,25 + 5 0,5 + 7 0,19 = 4,39 ;
D =12 0,06 + 22 0,25 + 52 0,5 + 72 0,19 − 4,392 = 3,6 ; σ |
x |
= |
3,6 =1,9. |
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
4) P{2 ≤ X ≤ 7} =P{X= 2} + P{X= 5} + P{X= 7} = 0,25 + 0,5 + 0,19 = 0,94. |
|||||||||||
ТАБЛИЦА 11.1.2 |
|
|
|
|
|
|
|
|
|
|
|
x |
F(x) |
|
|
y |
|
|
|
|
|
|
|
(−∞,1] |
0 |
|
1. |
|
|
|
|
|
|
|
|
|
0,81 |
|
|
|
|
|
|
|
|||
(1, 2] |
0,06 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
(2, 5] |
0,06 + 0,25 = 0,31 |
|
|
|
|
|
|
|
|
|
|
(5, 7] |
0,31 + 0,5 = 0,81 |
0,31 |
|
|
|
|
|
|
|
|
|
(7, ∞) |
0,81 + 0,19 =1 |
|
|
|
|
|
|
|
|
|
|
|
0,06 |
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
2 |
5 |
|
|
7 |
||
|
|
|
|
|
|
РИС. 11.1.2 |
|
|
|
|
|
Пример 11.1.2. Непрерывная сл. в. |
X имеет плотность распределения |
||||||||||
|
|
|
0 |
, если |
x ≤ 0; |
|
|
|
|
|
|
|
f |
|
|
|
|
0 < x ≤ 0,5; |
|
|
|
|
|
|
(x) = 8x , если |
|
|
|
|
|
|||||
|
|
|
|
, если |
x > 0,5. |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
Требуется: 1) построить кривую распределения; 2) найти F(x) , постро-
|
< X < |
1 |
|
ить график; 3) найти mx , Dx , σx ; 4) найти P 0 |
4 |
. |
|
|
|
|
Решение.
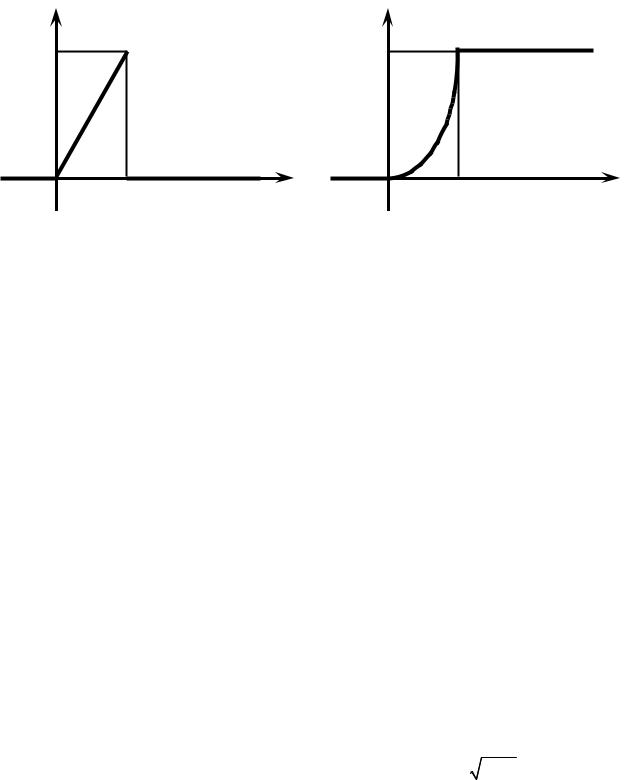
1) Построим график функции f (x) (Рис. 11.1.3) – кривую распределения случайной величины X
105
y |
y |
4 |
1 |
0 |
0,5 |
x |
0 |
0,5 |
|
x |
|
|
РИС. 11.1.3 |
|
РИС. 11.1.4 |
||||
2) Найдем F(x) в виде таблицы |
|
|
|
|
|||
|
|
|
|
|
|
|
ТАБЛИЦА 11.1.3 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
F(x) = ∫ f (x) dx |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
(−∞, 0] |
|
|
|
∫ 0 dx = 0, |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
|
|
(0, 0,5] |
|
|
∫ 0 dx + ∫8x dx = 4x2 , |
|
|
||
|
|
|
−∞ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,5 |
x |
|
0,5 |
|
(0,5; ∞) |
|
∫ |
0 dx + ∫ |
8x dx + ∫ 0 dx = |
4x2 |
=1. |
|
|
0 |
||||||
|
|
−∞ |
0 |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
Построим её график (Рис. 11.1.4)
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
8x3 |
|
|
|
|
|
|
|
|
|
|
3) |
|
2 |
|
= 0,33; |
|
|
|
|
|||||
mx = ∫x 8x dx = |
3 |
0 |
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0,5 |
|
|
|
||
|
0,5 |
|
|
|
|
2= 8x4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
Dx = ∫ x2 8xdx − 0,33 |
|
− 0,332= 0,02; σx = 0,02 = 0,13; |
||||||||||
|
0 |
|
|
|
|
4 |
|
0 |
|
|
|
||
|
0,25 |
|
|
|
|
0,25 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
4) P{0 < X < 0,25}= ∫ |
|
8x dx = 4x2 |
|
= 0,25 . |
|||||||||
|
|
||||||||||||
|
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
106
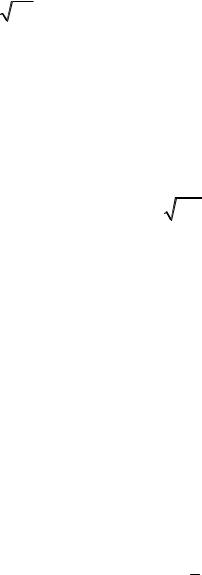
Пример 11.1.3. Случайная величина Х распределена по нормальному закону с параметрами m = −2, σ = 3. Записать плотность распределения случайной
величины.
Решение.
|
|
1 |
e− |
( x+2)2 |
|
|
f (x) = |
|
18 |
, |
− ∞ < x < ∞. |
||
|
2π |
|||||
3 |
|
X , изготовленной на станке, представляет |
||||
Пример 11.1.4. Длина детали |
||||||
собой случайную величину, распределенную по нормальному закону со сред-
ним значением 20 см и дисперсией 0,2 см2 . Найти вероятность того, что изме-
ряемая деталь имеет длину от 19,98 до 20,02 см.
Решение. |
|
|
|
|
|
|
|
|
|
|
||
Имеем X – длина |
|
|
детали, m = 20, σ = |
0,2 = 0,45 . Требуется |
найти |
|||||||
P{19,98 < X < 20,02 } = P{ |
|
|
X − 20 |
|
< 0,02 |
}. Пользуясь соответствующей |
фор- |
|||||
|
|
|||||||||||
мулой, получим P{ |
|
X − 20 |
|
|
|
|
|
0,02 |
|
= Φ(0,044) = 0,03 . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
< 0,02 }= Φ |
0,45 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 11.1.5. Устройство состоит из |
|
8 |
независимо работающих эле- |
|||||||||
ментов. Известна вероятность отказа каждого элемента за время T , равная р = 0,2 . Найти вероятность того, что за время T откажут два элемента.
Решение.
Имеем последовательность испытаний (наблюдений за работой элементов), удовлетворяющих схеме Бернулли:
1)испытания независимы;
2)два исхода: A – «элемент вышел из строя», А – «элемент работает»;
3)Р( А) = р = 0,2 в каждом испытании.
Случайная величина X – «число отказавших элементов» распределена по биномиальному закону с параметрами n =8, р = 0,2 .
Используя формулу Бернулли, получим
107