Тема 8. Функциональные ряды

∞

x −1

n

1)

Составим ряд из модулей членов степенного ряда ∑

.

2n (n2 +1)

n=0

2)

Применим к этому ряду признак Даламбера

D(x)= lim

x −1

n

2n (n2 +1)

=

x −1

.

n→∞ 2n+1

(n +1)2 +1

x −1

n

2

3)

Решим неравенство

D(x)<1

x −1

<1

x −1

< 2 .

2

Это неравенство с модулем имеет решение

−2 < x −1 < 2 −1 < x < 3 (рис. 8.1.1).

Полученный интервал симметричен относительно точки x0 =1.

−1

1

3

x

∞

(−1 −1)n

∞

(−1)n 2n

∞

(−1)n

∑

=∑

=∑

,

2n (n2 +1)

2n (n2 +1)

2

n=0

n=0

n=0 n

+1

в точке x = 3 ряд примет вид

=∑

21 .

∑ (3 −1)

n

∞

∞

n=0

2n (n2 +1)

n=0 n +1

∞

1

Ряд ∑

сходится по

признаку сравнения

со сходящимся рядом

2

n=0 n

+1

∞

1

∞

n

∑

, а знакочередующийся ряд

∑

(−1)

сходится абсолютно.

2

2

n=1 n

n=0 n

+

1

−1

1

3

x

Решение. Ряд Тейлора функции

f (x)

в окрестности точки x0 = 2 имеет

вид

f (x)= f (2)+

f ′(2)

(x − 2)+

f

′′(2)

(x

− 2)

2

+

f ′′′(2)

(x − 2)

3

+....

1!

2!

3!

Найдем первые три производные функции и вычислим значения функции

и ее производных при x0 = 2 . Получим:

f (x)= 3x2 + 3 + ex2 −4 f (2)=16,

f ′(x)= 6x + 2xex2 −4 f ′(2)=16,

f ′′(x)= 6 + 2ex2 −4 + 4x2ex2 −4 f ′′(2)= 24,

f ′′′(x)= 4xex2 −4 +8x3ex2 −4 + 8xex2 −4 f ′′′(2)=88.

Подставим полученные значения в ряд Тейлора

f (x)=16 +

16 (x − 2)+

24 (x − 2)2 +

88

(x − 2)3 +...

или

1!

2!

3!

f (x)=16 +16(x − 2)+12(x − 2)2 +

44 (x − 2)3

+....

3

Получено разложение функции

f (x) в ряд Тейлора в окрестности точки

ex =1 +

x

+

x2

+... +

xn

+...,

(−∞, ∞).

n!

1!

2!

x

значение

показателя степени

Подставим в

это разложение вместо

(−3x4 ), получим

e−3x

4

=1 +

(−3x4 )

+

(−3x4 )2

(−3x4 )n

1!

2!

+... +

n!

+... =

=1 −

3x4

+

32 x8 −... + (−1)n 3n x4n

+...

1!

2!

n!

Умножим левую и правую части равенства на

x2

3

x2

e−3x4 =

x2

1 −

3x4

x2

+

32 x8

x2

−...

+ (−1)n 3n x4n

x2

+....

3

3

1!

2!

3

3

n!

3

Выполним некоторые преобразования, общие для всех членов ряда: со-

кратим числитель и знаменатель на 3 и соберем степени x . Получим

x2

e−3x4 =

x2

−

x6

+

3x10

−... + (−1)n

3n−1 x4n+2

+...,

3

3

1!

2!

n!

∞

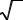
(x −1)

n

∞

(x + 4)

n

∞

(−1)

n

x

n

8.1.1.

∑

;

8.1.2.

∑

;

8.1.3.

∑

nn

;

n 2

n

n=0

3

(n

+1)

n=0

2

(3n +1)

n=0

(n +1)5

∞

(x +1)

n

∞

4

n

x

2n

∞

3)

2n+1

8.1.4.

∑

;

8.1.5.

∑

;

8.1.6.

∑n(x +2

;

(n + 2) n!

2n +1

n=0

n=0

n=0

n

+ 5

∞

x

n

∞

2)

n

∞

(x + 3)

n

8.1.7.

∑

;

8.1.8.

∑n!(x +

;

8.1.9.

∑

.

n

n=1 n +

n

n=0

3n + 4

n=0

2 (n +1)

Найти первые три члена разложения в ряд функции

f (x) в окрестности

точки x0 (по степеням (x − x0 ) :

8.1.10.

f (x) = e3x−x2 ,

x0 = 3 ;

8.1.11.

f (x) = cos(ln x),

x0 =1;

8.1.12.

f (x) = 3x2 + xsin(1 − x) ,

x0 =1;

8.1.13.

f (x) = 3x − cos(x2 − 4) ,

x0 = −2 .

Используя известные разложения функций в ряд, разложить в ряд по сте-

пеням x следующие функции:

x

x2

8.1.14.

xsin

;

8.1.15.

e−2x ;

8.1.16.

3cos3x2 ;

2

2

e

−x2

−1;

8.1.18.

x

2

8.1.19.

3

sin3x3 ;

8.1.17.

ln 1 −

;

4

x2

x2

1 − cos x

4

8.1.21.

3

x

x

2

e−5x

3

8.1.20.

;

x

ln 1 +

;

8.1.22.

.

x2

5

3