4.2.47. lim cos5x |
4.2.48. lim tg 2x |
|
|||||||||||||
x→0 sin 2x |
|
x→0 tg 5x |
|
|
|
||||||||||
|
|
5 2x |
4.2.50. |
|
+ |
2 3x |
|||||||||
4.2.49. lim 3 + |
|
|
lim 1 |
|
|
||||||||||
x→∞ |
x |
|
x→∞ |
|
x |
|
|||||||||
|
|
|
3 |
|
|
|
|
k |
mx |
||||||
4.2.51. lim (1 + 4x)x |
4.2.52. |
+ |
|
||||||||||||
lim 1 |
|
|
|||||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
x→∞ |
|
x |
|
||
|
|
x |
b |
|
|
|
7 4x |
||||||||
|
x |
|
|
4.2.54. |
− |
||||||||||
4.2.53. lim |
1 − |
|
|
lim 1 |
|
|
|||||||||
|
|
||||||||||||||
x→0 |
|
a |
|
x→∞ |
|
x |
|
||||||||
|
|
|
4 |
|
|
|
|
|
2 3x |
||||||
4.2.55. lim (1 −3x)x |
4.2.56. |
− |
|||||||||||||
lim 1 |
|
|
|
||||||||||||
|
|
||||||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
x→∞ |
|
5x |
|||
4.2.57. lim (1 + tg x)3 ctg x |
4.2.58. lim (1 − sin x)2 ctg x |
||||||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
4.3. Предел и непрерывность функции
4.3.1. Типовые примеры
Пример 4.3.1. Исследовать непрерывность функции в точке x0 = 0 :
а) y = x2 ; |
б) y = |
1 ; |
в) |
x +1, |
при x ≥ 0 |
; |
г) y = ln x . |
y = |
при x < 0 |
||||||
|
|
x |
|
x −1, |
|
|
|
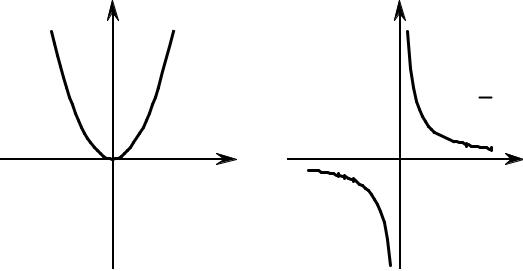
Решение. Построим графики данных функций (рис. 4.1.1) |
|
||||||
а) |
y |
|
|
б) |
y |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
y = x2 |
|
|
1 |
|
||
|
|
|
|
|
y = x |
|
|
|
0 |
|
x |
|
0 |
|
x |
45
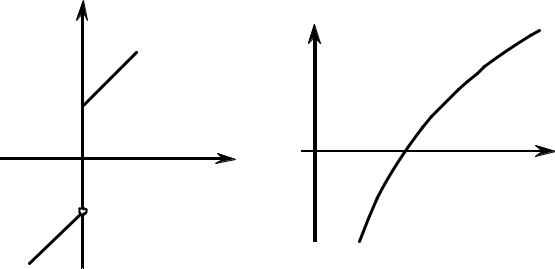
в) |
y |
|
г) y |
|
|
|
|
y = ln x |
|
||
|
|
|
|
|
|
1 |
y |
x +1, x ≥ 0 |
|
|
|
|
= |
|
|
|
|
|
0 |
x −1, x < 0 |
0 |
1 |
x |
|
x |
||||
|
|
|
|||
|
-1 |
|
|
|
|
РИС. 4.3.1
а) в точке x0 = 0 функция y = x2 является непрерывной, так как
lim x2 = 0 = f (0);
x→0
б) в точке x0 = 0 функция y = 1x не является непрерывной, так как f (0)
не существует; |
|
|
|
|
|
в) функция |
x +1, |
при |
x ≥ 0 |
; |
не является непрерывной, так как не |
y = |
при |
x < 0 |
|||
|
x −1, |
|
|
существует lim f (x);
x→0
г) функция y = ln x не является непрерывной в точке x0 = 0 , так как она не определена в этой точке.
Пример 4.3.2. Исследовать на непрерывность функцию
|
2 |
, |
при |
x ≤ 0 |
x |
|
|||
f (x)= |
+1, |
при |
x < 0 |
|
2x |
||||
|
|
|
|
|
в точке x0 = 0 .
Решение. Найдем предел слева, предел справа и значение функции в точке x0 = 0 :
f (x − 0)= lim |
f (x )= lim x2 = 0 , |
||
0 |
x→x0 |
−0 |
x→0−0 |
|
|||
|
|
|
46 |
f (x0 |
+ 0) = lim f (x) = |
lim 2x +1 =1 |
|
x→x0 +0 |
x→0+0 |
|
f (0)= x2 |
= 0 . |
|
x = 0 |
|
Так как нарушено условие непрерывности функции f (x0 − 0)≠ f (x0 + 0),
то функция не является непрерывной в точке x0 = 0 .
Пример 4.3.3. Доказать непрерывность функции y = f (x) в точке x0 = 0
или установить характер разрыва функции в этой точке:
|
|
sin x |
|
sin x |
, |
если |
x ≠ 0 |
|
||||
а) |
y = |
|
|
x |
; |
|||||||
x |
; б) y = |
|
|
|
|
|
|
|||||
|
|
|
|
1, |
|
если x = 0 |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
0, |
если |
x < 0 |
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
в) |
|
|
|
|
; г) y = 2 x . |
|
||||||
y = |
если |
|
|
|||||||||
|
|
ex , |
x ≥ 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
а) Функция |
|
y = |
sin x |
в точке x = 0 не определена, но |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|||
lim sin x =1 (первый замечательный предел), следовательно, точка x0 = 0 – точ-
x→0 x
ка устранимого разрыва функции.
б) По сравнению со случаем а), функция определена в точке x0 = 0 и ее значение f (0)=1 совпадает с пределом функции в этой точке, значит, функция
непрерывна в точке x0 = 0 . |
|
|
|
|
|||
в) Найдем пределы слева и справа в точке x0 = 0 |
|
|
|
||||
f (0 − 0)= 0, |
f (0 + 0)= lim ex =1, |
f (0)=1. |
|||||
|
|
|
|
x→0+0 |
|
|
|
Так как эти пределы не равны, то x0 = 0 – скачок функции. |
|||||||
1 |
|
|
|
|
|
|
|
г) Функция y = 2 |
x |
не определена при x = 0 , а |
|
|
|
||
1 |
|
1 |
|
||||
f (0 − 0)= lim 2 |
|
= 2−∞ = 0, f (0 + 0)= lim |
2 |
|
= 2∞ = ∞, |
||
x |
x |
||||||
x→0−0 |
x→0+0 |
||||||
следовательно x0 = 0 – точка бесконечного разрыва функции.
47
4.3.2. Контрольные вопросы
1)Сформулируйте определение непрерывной в точке функции.
2)Сформулируйте второе определение непрерывной в точке функции.
3)Что называется пределом слева и справа функции f (x) в точке x0 ?
4)Сформулируйте необходимое и достаточное условие непрерывности функции в точке.
5)Что называется точкой разрыва функции?
6)Сформулируйте свойства непрерывных функций.
7)Сформулируйте свойства функции, непрерывной на отрезке.
4.3.3. Практические задания
4.3.1. Найти область определения функций f (x):
а) f (x) = 3x −1 |
б) f (x)= |
|
1 |
|
|
|
||
x2 +1 |
|
|
||||||
в) f (x)= |
2x |
г) f (x)= |
|
1 |
|
|
+ lg(5x +10) |
|
x2 − 3x + 2 |
|
−1 |
||||||
|
|
|
x |
|
||||
При каких значениях переменной x эта функция непрерывна? |
||||||||
4.3.2. Найти левосторонний и правосторонний пределы функции:
x, |
x ≤1 |
f (x)= |
, x >1 |
(x −1)2 |
|
|
|
в точке x0 =1. Сделать вывод о непрерывности функции в этой заданной точке.
4.3.3. Исследовать на непрерывность функцию
sin x, |
x < π |
||
|
|
|
2 |
f (x)= |
|
|
|
|
1, |
x ≥ |
π |
|
2 |
||
|
|
|
|
4.3.4. По графику функции y = f (x) |
определить интервалы непрерывности и |
||
найти точки разрыва, дать их классификацию:
48
y
y
|
f (x2 ) |
|
|
f (x2 ) |
|
|
|
|
|
|
|
|
|
|
|
x1 |
0 |
x |
x1 |
0 |
x2 |
x3 |
x |
x |
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
РИС. 4.3.2 |
|
|
|
|
|
|
|
РИС. 4.3.3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.3.5. Найти область определения функции |
f (x), область непрерывности и ис- |
||||||||||||||||||
следовать характер точек разрыва: |
|
|
|
|
|
|
|
||||||||||||
а) f (x)= |
|
x2 |
б) |
f (x)= |
x2 − 9 |
|
в) |
f (x)= |
x + 3 |
||||||||||
|
|
|
|
|
|
|
|
x2 − x − 2 |
|
||||||||||
x − 3 |
x − 3 |
||||||||||||||||||
г) f |
( |
x |
) |
= |
x2 + 8x +12 |
|
д) |
f (x)= |
|
x − 2 |
|
|
|
|
|||||
|
x2 − 3x + 2 |
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
x + 2 |
|
|
|
|
|
|||||||||
4.3.6. Найти точки разрыва функции |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
x (−∞, 0) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
f (x)= |
|
|
x [0, ∞) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x + 2, |
|
|
|
|||||
иисследовать их характер. Построить график функции.
4.3.7.Исследовать на непрерывность функции:
|
|
2 |
−1, x (−∞, 2) |
|
|
|
x |
|
x |
|
|
f (x)= |
|
||||
а) f (x)= |
2x − 3, x [2, ∞) |
б) |
|
|
|
|||
|
x |
|
||||||
|
|
|||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Построить графики этих функций. |
|
|
|
|
|
4.3.8. Дана функция |
|
|
|
|
|
x2 |
|
− 4 |
при |
x ≠ 2 |
|
|
|
|
|
||
|
− 2 |
||||
f (x)= x |
|
|
|||
|
A |
|
при |
x = 2 |
|
|
|
||||
Как следует выбрать значение функции A = f (2), чтобы дополненная таким образом функция f (x) была непрерывна при x = 2?
4.3.9. Найти область определения и область непрерывности функции:
а) f (x)= lg(1 − x)+ 2 + x |
б) f (x)= |
sin x |
|
x2 − 2x +1 |
|
||
|
49 |
|
|