Файловый архив студентов. Файловый архив студентов.
1328 вузов, 5500 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Казанский кооперативный институт (филиал РУК)
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
ПланыПЗ_Математ_036401.pdf
Скачиваний:
38
Добавлен:
26.02.2016
Размер:
942 Кб
Скачать
☆
►Содержание►

Тема 6. Интегральное исчисление

6.1. Решение задач на нахождение неопределенных интегралов. Нахождение неопределенных интегралов различными методами

6.1.1. Типовые примеры

Пример 6.1.1. Вычислить интегралы, используя таблицу интегралов, свойства линейности и свойство:

 

если ∫ f (x)dx = F (x) + C , то ∫ f (ax + b)dx =

1 F (ax + b)+ C .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

а) J

=

∫

 

3cos x − 4

 

+ 5 dx ;

 

 

 

 

 

б)

 

 

J

 

 

 

=

∫

3

x2

−

2

+ 3x

dx ;

 

 

 

 

 

 

 

2

 

 

1

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) J3 = ∫(sin 2x − 2e1−3x )dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) J

= 3

∫

cos xdx − 4

∫

dx

+ 5

∫

dx =3sin x − 4ln

 

x

 

+ 5x + C ;

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

dx − 2∫x−3dx + 3∫xdx =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б) J2 = ∫x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

x−2

 

x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

 

x

3

 

−

2

+ 3

+ C =

3

3

x

5

+

 

1

+

3

x

2

+ C ;

 

 

 

 

 

 

 

5

 

 

−2

2

5

 

 

 

 

 

x2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

в) для вычисления интеграла воспользуемся свойством 3 и таблицей интегралов, получим

J3 = ∫sin 2xdx − 2∫e1−3xdx =

= −12 cos 2x − 2 −13 e1−3x + C = 32 e1−3x − 12 cos 2x + C.

Пример 6.1.2. Вычислить ∫e1−4xdx .

Решение. Внесем под знак дифференциала функцию u =1 − 4x , получим

67

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u =1 − 4x

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

∫

1−4x

 

 

 

=

∫

e

−

1

1

e

u

+ C = −

1

1−4x

+ C .

e

dx = du = −4dx

 

 

4

du = −

4

 

4

e

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx = − 4 du

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 6.1.3. Вычислить ∫(x + 2)cos xdx .

Решение. Для вычисления этого интеграла воспользуемся методом интегрирования по частям

 

 

 

 

 

 

 

 

+ 2,

 

 

 

 

du

 

= (x +

 

′

 

 

 

 

 

 

 

 

u = x

 

 

 

 

 

2) dx = dx,

 

=

∫

(x + 2)cos xdx =

 

 

 

 

 

 

 

 

 

 

 

∫

dv =

∫

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dv = cos xdx, v =

 

 

cos xdx = sin x

 

 

 

= (x + 2)sin x − ∫sin xdx = (x + 2)sin x + cos x + C.

 

 

Пример 6.1.4. Вычислить интеграл ∫

3x4 − x3 + 3x2 +1

 

 

 

 

 

 

 

x

3

 

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+ x

 

 

Решение. Рациональная дробь, стоящая под знаком интеграла, является

неправильной, поэтому выделим целую часть

 

 

 

 

 

 

 

 

 

 

−

3x4 − x3 + 3x2

 

+1

 

x3

+ x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3x4

 

+ 3x2

 

 

 

 

 

 

 

3x

−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

−x3

 

 

+1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−x3

− x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3x4

− x3

+ 3x2 +1

x +1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получим

=

3x −

1 +

 

 

x

 

+

1

.

 

 

 

 

 

 

x3

 

+ x

 

 

x3

 

+ x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Разложим знаменатель дроби на множители x3 + x = x(x2 +1).

Правильную рациональную дробь разложим в сумму простейших дробей

x +1

 

x +1

A

 

Bx + C

 

=

 

=

 

+

x2 +1 .

x3 + x

x(x2 +1)

x

Правую часть приведем к общему знаменателю и приравняем числители дробей

x +1 = A(x2 +1)+ (Bx + C )x = Ax2 + A + Bx2 + Cx . 68

Чтобы получить значения коэффициентов, приравняем коэффициенты при одинаковых степенях x , получим

x0

 

1 = A,

 

x1

 

1 = C,

x2

 

0 = A + B B = −A = −1.

Используя полученные коэффициенты, запишем разложение подынтегральной функции

3x4 − x3 + 3x2 +1

= 3x −1

+

1

+

−x +1

.

x3

+ x

x

x2

+1

 

 

 

 

Подставим это разложение под знак интеграла и вычислим его

∫

3x4

− x3 + 3x2 +1

 

3x −1

+

1

+

−x +1

 

x

3

+ x

dx = ∫

x

x

2

dx =

 

 

 

 

 

 

 

 

 

+1

=3∫xdx − ∫dx + ∫dxx − ∫xxdx2 +1 + ∫x2dx+1 =

=32x2 − x + ln x − 12 ln (x2 +1)+ arctg x + C .

Пример 6.1.5. Вычислить интеграл ∫

x + 2

dx .

 

 

x + 3 x2

Решение. Наименьшее общее кратное показателей корней 2 и 3 равно 6. Вычислим интеграл методом замены переменной

 

 

 

 

 

 

 

 

6

x

= t x

= t

6

 

 

 

 

 

 

(t3 + 2)6t5dt

 

∫

x + 2

 

 

 

 

 

 

 

 

 

 

 

 

∫

 

 

 

 

dx

=

dx = 6t5dt

 

 

x = t3

 

=

t

6

+ t

4

=

x + 3

 

 

 

 

 

x2

 

 

 

3 x2 = t4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 6∫

t4 + 2t

dt = 6∫

 

 

−1 +

2t +1

 

 

 

 

 

 

t

2

+1

 

t2

t

2

+

dt =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2t

 

 

 

1

 

 

 

 

 

 

 

 

 

 

=

6∫ t2

 

−1 +

 

 

 

 

+

 

 

 

 

dt =

 

 

 

 

 

 

 

 

t

2

+1

t

2

+1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 6

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+ C

=

 

 

 

 

 

t

 

 

− t + ln (t2 +1)+ arctgt

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 2 x − 66 x + 6ln (3 x +1)+ 6arctg 6 x + C .

69

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

Пример 6.1.6. Вычислить интеграл ∫ 1 +

 

 

 

cos xdx .

sin

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

Решение. Используя замену sin x = t , получим

 

 

1

 

 

 

 

 

 

1

 

 

 

 

 

 

 

∫ 1 +

 

 

 

cos xdx = ∫ 1 +

 

 

 

 

d (sin x)={sin x = t}=

sin

2

 

 

sin

2

 

 

 

x

1

 

1

 

 

x

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= ∫ 1 +

 

 

dt = t −

 

+ C

= sin x −

 

 

+ C .

 

t

2

t

sin x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 6.1.7. Вычислить интеграл ∫sin2 5xdx .

Решение.

∫sin2 5xdx = ∫1 − cos102 xdx = 12 ∫dx − 12 ∫cos10xdx =

=2x − 201 sin10x + C .

6.1.2.Контрольные вопросы

1) Какая функция называется первообразной для функции f (x)? Сколько

первообразных имеет данная функция?

2) Что называется неопределенным интегралом от функции f (x)? Каков его геометрический смысл?

3)Какие свойства связывают операции дифференцирования и интегрирования?

4)Сформулируйте свойства линейности неопределенного интеграла.

5)Чему равен интеграл ∫ f (ax + b)dx , если ∫ f (x)dx = F (x)+ C ?

6)Запишите формулу интегрирования по частям.

7)Перечислите виды интегралов, берущихся по частям.

8)По каким правилам разбивается подынтегральное выражение на множители u и dv ?

9)Что называется рациональной дробью? Какая дробь называется правильной, неправильной? Что значит, выделить целую часть?

10)Какие дроби называются простейшими? Какой вид имеет разложение правильной дроби в сумму простейших дробей?

11)Какой вид имеет формула замены переменной в неопределенном интеграле?

6.1.3.Практические задания

6.1.1.Вычислить интегралы:

70

 

∫

(

3x4

 

 

 

 

 

2x − 3 +

 

4

 

 

а)

− 2sin x +1 dx ;

б)

 

 

 

dx ;

 

 

 

 

 

 

)

 

∫

x

4 − x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) ∫(cos(x + 2)− ex+1 )dx ;

г) ∫

 

dx

 

 

 

 

 

;

 

 

 

 

sin2 (3x)

 

 

 

 

д)

∫

 

 

 

 

3dx

;

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

2x +1 −

 

 

 

 

 

 

2

 

 

 

 

 

 

cos

(3x +1)

 

е) ∫

(2x −1)

3

dx ;

 

 

 

 

 

 

 

 

 

 

 

 

 

∫

 

x

 

 

ж)

sin

 

+

2x dx ;

3

 

 

 

 

6.1.2. Вычислить интегралы:

а) ∫

8xdx

;

б)

x

2

+ 4

 

 

 

 

г) ∫6x2ex3 dx ;

д)

з) ∫(5x + 3)6dx .

∫(x2 + 3)xdx ;

в)

∫

x3dx

;

е)

x4 + 2

 

∫4xsin (x2 )dx ;

3x2dx

∫sin2 (x3 ).

ж) ∫sin (ln x)dxx ;

 

 

7

 

 

 

 

 

 

4exdx

 

 

 

з) ∫ln

xxdx ;

 

и) ∫

 

 

.

 

cos2 (ex )

6.1.3. Вычислить интегралы, используя формулы d(sin x) = cos xdx ,

 

 

 

а) ∫cos3 xsin xdx ;

б) ∫2sin x cos xdx ;

 

в) ∫

 

 

sin xdx

 

 

;

 

4

+ cos

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

г) ∫ctg4 x

dx

д) ∫

 

dx

 

е) ∫3sincosxdxx .

 

 

;

 

 

;

 

 

 

cos2 x(3 + tg x)

sin2 x

6.1.4. Вычислить интегралы, используя формулы

 

 

 

 

 

 

 

 

 

 

arcsin x

 

 

 

 

 

3

 

 

 

 

 

 

 

 

а) ∫

e

dx ;

 

 

б) ∫

arctg x

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 − x2

 

 

1 + x2

 

 

 

 

 

 

 

6.1.5. Вычислить интегралы, используя метод непосредственного интегрирования:

 

б)

 

dx

 

;

 

5dx

 

2cos xdx

 

 

∫sin2

 

 

в) ∫

 

 

а) ∫3 1 + 3xdx ;

 

x

 

 

x(9 + ln2 x)

;

г) ∫

sin5 x

;

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

71

 

 

 

 

 

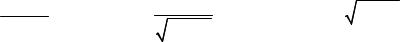
4 xdx ∫ x3dx

д) ∫x3ex dx ; е) ∫4 + x4 ; ж) 1 − x8 ; з) ∫ex 1 + ex dx .

6.1.6. Вычислить интегралы от произведения многочленов на функции sin ax ,

cos ax , eax

методом интегрирования по частям:

 

 

 

 

 

а) ∫xcos xdx ;

 

 

б) ∫(x + 2)exdx ;

 

 

 

 

в) ∫(1 − x)sin 2xdx ;

 

 

г) ∫(1 − 4x)cos3xdx .

 

 

 

6.1.7. Вычислить интегралы, содержащие функции ln x , arctg x ,

arcsin x мето-

дом интегрирования по частям:

 

 

 

 

 

 

 

а) ∫ln xdx ;

б) ∫x3 ln xdx ;

 

в) ∫arctg xdx ;

г) ∫arcsin xdx .

Вычислить интегралы:

 

 

 

 

 

 

 

6.1.8. ∫(2x +1)e−3xdx ;

6.1.9. ∫

1

ln xdx ;

6.1.10. ∫(2x + 3)cos 2xdx ;

2

 

 

 

x

 

 

 

 

 

6.1.11. ∫x3x dx ;

6.1.12. ∫xarctg xdx ;

6.1.13. ∫

xdx

 

;

cos

2

 

 

 

 

 

 

 

 

x

6.1.14. ∫x2 cos xdx ;

6.1.15. ∫ln2 xdx ;

6.1.16. ∫ln (x2 +1)dx ;

6.1.17. ∫ex sin xdx .

Вычислить интегралы методом интегрирования по частям:

6.1.18. ∫xe−xdx ;

6.1.19. ∫xsin 2xdx ;

6.1.20. ∫xln xdx ;

6.1.21. ∫(2 − 5x)cos3xdx ;

6.1.22. ∫arctg 2xdx ;

6.1.23. ∫x2e3xdx .

6.1.24. Вычислить интегралы:

 

 

а) ∫sin3 x cos xdx ;

б) ∫cos5 2x sin 2xdx ;

6.1.25. Вычислить интегралы:

а)

∫sin5 x cos3 xdx ;

б)

∫cos3 3x sin3 3xdx ;

г)

∫sin

2

4x cos

3

4xdx ;

д)

∫

cos3 xdx

;

 

 

sin4 x

в)

е)

∫

∫

sin3 xdx ;

2cos3 5xdx .

72

6.1.26. Вычислить интегралы:

 

 

 

а) ∫sin2 3xdx ;

б) ∫cos2 4xdx ;

в) ∫sin2

x

dx ;

2

г) ∫sin2 x cos2 xdx ;

д) ∫sin4 2xdx ;

е) ∫2sin2 8xdx .

6.1.27. Вычислить интегралы от рациональных дробей, имеющих простые корни в знаменателе:

а) ∫

3x + 4

б) ∫

x2 − x + 3

 

 

dx ;

 

 

dx ;

(x −1)(x + 6)

x(x −1)(x + 2)

г) ∫

 

4x +1

д) ∫

x5 + x4 −8

 

 

 

dx ;

 

dx .

x2 − x − 2

 

x3 − 4x

6.1.28. Вычислить интегралы от рациональных дробей, имеющих кратные корни в знаменателе:

 

6x − 4

 

dx

 

3

 

 

x2 + 2x + 2

 

а) ∫

 

dx ;

б) ∫

 

;

в) ∫

x +1

dx ;

г) ∫

 

dx .

 

 

(x + 2)3

x3 + 2x2

x4 − x2

x3 − x2

6.1.29. Вычислить интегралы от рациональных дробей, имеющих комплексные корни в знаменателе:

а) ∫

 

4x + 3

б) ∫

2x −1

 

x4

− x2 + x

−12

 

 

dx ;

 

dx ;

в) ∫

 

 

 

 

dx .

x3 + 9x

(x + 2)(x2 +1)

 

 

 

 

 

 

x3 + 4x

 

6.1.30. Вычислить

интегралы

от функций,

рационально

зависящих от

m

x

α

,

p

x

β

, ... :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

dx

 

dx

 

 

 

dx

а) ∫

 

 

 

;

б) ∫

 

 

 

; в) ∫

 

 

 

;

г) ∫

 

 

.

6(

x − 3 x )

4 x (

x + 4)

x (

x + 24 x )

3 x2 + x

6.1.31. Вычислить интегралы от иррациональных функций:

 

 

 

 

 

 

 

dx

 

 

 

dx

 

в) ∫

 

 

dx

а) ∫

 

 

;

б) ∫

 

 

;

 

 

.

 

 

 

 

 

 

( x +1)3 (x + 2)

x(

3 x + 2)

 

x ( x − 4 x )

 

73

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности