
- •МАТЕМАТИКА
- •ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
- •ВВЕДЕНИЕ
- •Раздел. I. ЛИНЕЙНАЯ АЛГЕБРА
- •Тема 1. Линейная алгебра
- •1.1. Вычисление определителей
- •1.1.1. Типовые примеры
- •1.1.2. Контрольные вопросы
- •1.1.3. Практические задания
- •1.2. Действия над матрицами
- •1.2.1. Типовые примеры
- •1.2.2. Контрольные вопросы
- •1.2.3. Практические задания
- •1.3. Решение систем линейных алгебраических уравнений.
- •1.3.1. Типовые примеры
- •1.3.2. Контрольные вопросы
- •1.3.3. Практические задания
- •Тема 2. Векторная алгебра
- •2.1. Векторы. Линейные операции над векторами.
- •2.1.1. Типовые примеры
- •2.1.2. Контрольные вопросы
- •2.1.3. Практические задания
- •2.2. Произведения векторов
- •2.2.1. Типовые примеры
- •2.2.2. Контрольные вопросы
- •2.2.3. Практические задания
- •2.3. Комплексные числа
- •2.3.1. Типовые примеры
- •2.3.2. Контрольные вопросы
- •2.3.3. Практические задания
- •Тема 3. Аналитическая геометрия
- •3.1. Основные задачи аналитической геометрии
- •3.1.1. Типовые примеры
- •3.1.2. Контрольные вопросы
- •3.1.3. Практические задания
- •3.2. Кривые второго порядка
- •3.2.1. Типовые примеры
- •3.2.2. Контрольные вопросы
- •3.2.3. Практические задания
- •Раздел. II. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •Тема 4. Предел функции
- •4.1. Элементы теории множеств. Понятие функции
- •4.1.1. Типовые примеры
- •4.1.2. Контрольные вопросы
- •4.1.3. Практические задания
- •4.2. Теория пределов
- •4.2.1. Типовые примеры
- •4.2.2. Контрольные вопросы
- •4.2.3. Практические задания
- •4.3. Предел и непрерывность функции
- •4.3.1. Типовые примеры
- •4.3.2. Контрольные вопросы
- •4.3.3. Практические задания
- •Тема 5. Дифференциальное исчисление
- •5.1. Вычисление производных
- •5.1.1. Типовые примеры
- •5.1.2. Контрольные вопросы
- •5.1.3. Практические задания
- •5.2. Исследование функций на экстремумы и интервалы монотонности
- •5.2.1. Типовые примеры
- •5.2.2. Контрольные вопросы
- •5.2.3. Практические задания
- •5.3. Исследование функций двух переменных
- •5.3.1. Типовые примеры
- •5.3.2. Контрольные вопросы
- •5.3.3. Практические задания
- •Тема 6. Интегральное исчисление
- •6.1. Решение задач на нахождение неопределенных интегралов. Нахождение неопределенных интегралов различными методами
- •6.1.1. Типовые примеры
- •6.1.2. Контрольные вопросы
- •6.1.3. Практические задания
- •6.2. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов
- •6.2.1. Типовые примеры
- •6.2.2. Контрольные вопросы
- •6.2.3. Практические задания
- •7.1. Сходимость знакоположительных рядов
- •7.1.1. Типовые примеры
- •7.1.2. Контрольные вопросы
- •7.1.3. Практические задания
- •7.2. Исследование сходимости знакочередующихся рядов
- •7.2.1. Типовые примеры
- •7.2.2. Контрольные вопросы
- •7.2.3. Практические задания
- •Тема 8. Функциональные ряды
- •8.1. Нахождение интервала и радиуса сходимости степенных рядов
- •8.1.1. Типовые примеры
- •8.1.2. Контрольные вопросы
- •8.1.3. Практические задания
- •Раздел. IV. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- •Тема 9. Численные методы
- •9.1. Нахождение корней уравнений итерационным методом
- •9.1.1. Типовые примеры
- •9.1.2. Контрольные вопросы
- •9.1.3. Практические задания
- •9.2. Примеры численного интегрирования
- •9.2.1. Типовые примеры
- •9.2.2. Контрольные вопросы
- •9.2.3. Практические задания
- •9.3. Примеры численного интерполирования
- •9.3.1. Типовые примеры
- •9.3.2. Контрольные вопросы
- •9.3.3. Практические задания
- •Раздел. V. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- •Тема 10. Случайные события
- •10.1. Задачи на вычисление классической вероятности и относительной частоты
- •10.1.1. Типовые примеры
- •10.1.2. Контрольные вопросы
- •10.1.3. Практические задания
- •Тема 11. Случайные величины
- •11.1. Законы распределения случайной величины
- •11.1.1. Типовые примеры
- •11.1.2. Контрольные вопросы
- •11.1.3. Практические задания
- •Тема 12. Математическая статистика
- •12.1. Методы математической статистики
- •12.1.1. Типовые примеры
- •12.1.2. Контрольные вопросы
- •12.1.3. Практические задания
- •РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
5.1.8. lim 1 − cos x .
x→0 x2
5.1.10. lim ex − e−x .
x→0 x2
5.1.12. lim e7 x − ex . x→0 sin 2x
5.1.9. |
lim |
ex −1 |
. |
|
|
|
|||
|
|
x |
|
|
|
|
|||
|
x→0 |
|
|
|
|
|
|
|
|
5.1.11. |
lim |
ex − cos x |
. |
|
|||||
|
x + sin x |
|
|||||||
|
x→0 |
|
|
|
|||||
5.1.13. |
lim |
|
|
1 + x3 |
|
|
. |
||
|
|
|
|
1) |
|||||
|
x→−1 sin (x + |
|
|||||||
5.2. Исследование функций на экстремумы и интервалы монотонности
5.2.1. Типовые примеры
Пример 5.2.1. Найти интервалы монотонности и экстремумы функции
y = |
4x − 6 |
. |
|
||
|
(x −1)2 |
|
Решение.
1.Область определения: Dy = (−∞,1) (1, ∞).
2.Вычислим производную
|
y |
′ |
|
4(x −1)2 − (4x − 6) 2(x −1) |
|
4(2 − x) |
|
|
||||
|
= |
|
|
(x −1)4 |
= (x −1)3 |
|
|
|||||
|
|
|
|
|
|
|||||||
и найдем критические точки: |
|
|
|
|
|
|
|
|||||
|
y′ = 0 4(2 − x) = 0 x = 2 – критическая точка. |
|
||||||||||
3. Исследуем функцию. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА 5.2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
(−∞,1) |
|
|
|
1 |
|
(1, 2) |
|
2 |
(2, ∞) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
− |
|
|
|
|
∞ |
|
+ |
|
0 |
− |
|
f (x) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
точка разрыва |
|
|
|
|
max |
|
|
|
|
|
|
|
|
||||||
На |
интервалах (−∞ |
,1), |
(2, ∞) функция убывает, на интервале (1,2) функ- |
|||||||||
ция возрастает. Точка x = 2 – точка максимума функции. |
|
|
||||||||||
4. max f (x) = f (2) = 2 . |
|
|
|
|
|
|
|
|||||
55
Пример 5.2.2. Найти |
наибольшее и наименьшее значения функции |
|
y = x5 − 5x4 + 5x3 + 3 на отрезке [−1, 2] . |
||
Решение. |
|
|
1. |
y′ = 5x4 − 20x3 +15x2 = 5x2 (x2 − 4x + 3) . Найдем критические точки. |
|
|
y′ = 0 5x2 (x2 − 4x + 3) = 0 x1 = 0, x2 =1, x3 = 3. |
|
Точку x3 =3 не рассматриваем, так как 3 [−1, 2]. |
||
2. |
Находим: f (0) = 3, |
f (1) = 4, f (−1) = −8, f (2) = −5 . |
3. |
Сравнивая полученные значения функции, делаем вывод: |
|
наибольшее значение M = 4 = f (1) ,
наименьшее значение m = −8 = f (−1) .
Пример 5.2.3. Найти интервалы выпуклости, вогнутости и точки переги-
ба графика функции y = x4 − 6x2 + 5.
Решение
1. Dy = (−∞, ∞) .
2. y′ = 4x3 −12x, y′′ =12x2 −12
y′′ = 0 12 (x2 −1) = 0 x1 = −1, x2 =1 –
критические на перегиб точки. 3. Заполним таблицу.
|
|
|
|
|
|
|
|
ТАБЛИЦА 5.2.2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
(−∞, −1) |
|
–1 |
|
(–1, 1) |
1 |
|
|
|
|
(1, ∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
+ |
|
0 |
|
− |
0 |
|
|
|
|
+ |
|
f (x) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) |
|
вогнут. |
|
т. перег. |
|
выпукл. |
т. перег. |
|
|
|
вогнут. |
||
|
|
|
|
|
|
|
|
|
|
||||
График вогнутый на (−∞, −1) , (1, ∞) . |
|
|
|
|
|
|
|||||||
График выпуклый на (–1, 1). |
|
|
|
|
|
|
|
|
|||||
4. |
f (−1) = 0, f (1) = 0, |
M1(−1,0), M2 (1,0) – точки перегиба. |
|
|
|
|
|||||||
Пример 5.2.4. Провести общее исследование функции y = |
x2 |
|
|
. |
|||||||||
x |
− |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
56 |
|
|
|
|
|
|
||
Решение
1. Dy = (−∞,1) (1, ∞) , x =1 – точка бесконечного разрыва функции, так
как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
x |
2 |
|
|
= ∞, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x =1 – уравнение вертикальной асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2. |
y = k x + b , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = lim |
|
f (x) |
= lim |
|
x |
|
=1, |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ ∞ |
|
x |
|
|
|
x→ ∞ x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
( f (x) = k x)= lim |
|
|
|
x2 |
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||
|
|
b = lim |
|
|
|
|
− x |
= lim |
|
|
|
|
=1, |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x→ ∞ |
|
|
|
|
|
|
|
|
|
|
|
x→ ∞ |
x −1 |
|
|
|
x→ ∞ x −1 |
|
|
|
||||||||||||||||
y = x +1 – уравнение наклонной асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3. |
f (−x) = |
|
(−x)2 |
|
= − |
x2 |
|
≠ ± f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
−x − |
1 |
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Функция свойствами четности, нечетности не обладает, не периодичная. |
|||||||||||||||||||||||||||||||||||||||||
4. f (x) = 0 |
|
|
x2 |
= 0 x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА 5.2.3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
(−∞, 0) |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
(0,1) |
|
|
|
|
|
1 |
|
|
|
|
(1, ∞) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
∞ |
|
|
+ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
′ |
2x (x −1) − x2 |
|
|
x2 − 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5. f (x) = |
|
|
(x −1)2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
(x −1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
f |
′ |
x |
2 |
− 2x |
= 0 x1 = 0, |
x2 = 2 – критические точки. |
|
||||||||||||||||||||||||||||||||||
(x) = 0 |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА 5.2.4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
(−∞, 0) |
|
|
|
|
|
|
|
0 |
|
|
|
|
(0,1) |
|
|
|
|
1 |
|
|
|
(1,2) |
|
|
|
2 |
|
(2, ∞) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
− |
|
|
|
|
|
∞ |
|
|
|
|
− |
|
|
|
0 |
|
+ |
||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
разр. |
|
|
|
|
|
|
|
min |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
max |
f (x) = f |
(0) = 0 , |
|
min f (x) = |
f (2) = 4 . |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
|
′′ |
|
|
(2x − 2) (x −1)2 − (x2 − 2x) 2 (x −1) |
= |
|
|
|
|
|
|
|
|
||||||
|
f (x) = |
|
|
(x −1)4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
2 (x −1) ((x −1) (x −1) − (x2 − 2x)) |
= |
2 (x2 |
− 2x +1 − x2 |
+ 2x) |
= |
|
2 |
|
, |
|||||||||
′′ |
|
|
(x |
−1)4 |
|
|
(x |
−1)3 |
|
|
(x − |
1)3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f |
|
|
точек перегиба нет, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(x) ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА 5.2.5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1, ∞) |
|
||||
|
|
|
x |
|
|
(−∞,1) |
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
′′ |
|
|
− |
|
|
|
∞ |
|
|
|
|
+ |
|
|
|||
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
вогнутый |
|
||||||||
|
|
f (x) |
|
выпуклый |
|
|
разрыв |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
7. Построим |
график функции (Рис |
. 5.2.1). |
|
|
|
|
|
|
|
|
|
|||||||
y
4 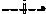
0
1 |
2 |
x |
|
|
РИС. 5.2.1
5.2.2. Контрольные вопросы
1)Дайте определения возрастающей и убывающей на интервале функций, постройте их графики.
2)Сформулируйте достаточные признаки возрастания и убывания функции.
3)Дайте определения точек максимума и минимума функции.
4)Сформулируйте необходимое условие экстремума. Будет ли необходимое условие достаточным?
5)Какая точка называется критической?
58
