
- •Математическое моделирование Учебное пособие
- •Донецк 2006
- •Содержание
- •Введение
- •1. Построение экспериментальных законов распределения
- •1.1. Общие положения
- •1.2. Статистические критерии согласия
- •Г) Критерий согласия Романовского
- •1.3. Построение закона Пуассона
- •1.4. Построение показательного закона
- •1.5. Построение нормального закона
- •2. Модели оптимизации
- •2.1. Принципы формирования моделей оптимизации
- •Задача производственного планирования
- •Задача оптимальной загрузки оборудования
- •Задача о смесях
- •Транспортная задача
- •2.2. Графический метод решения задачи линейного программирования
- •Алгоритм графического метода решения злп
- •2.3. Универсальный метод решения линейных задач оптимизации
- •Алгоритм симплекс-метода решения злп
- •Пример 2.3.1. Решить злп (2.2.1), (2.2.5) симплекс-методом.
- •Критерий оптимальности опорного плана
- •Переход к следующей симплекс-таблице осуществляют по правилам:
- •2.4. Двойственная задача линейного программирования
- •Свойства двойственных задач
- •2.5. Методы анализа конфликтных ситуаций с помощью матричных игр
- •Алгоритм принципа максимина (минимакса)
- •Решение. Этаматричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.
- •Последовательность действий при решении игры
- •3. Регрессионный анализ
- •3.1. Однофакторные модели
- •3.1.1. Построение однофакторных моделей
- •3.1.2. Оценка качества моделей
- •Свойства коэффициента корреляции
- •Построение доверительного интервала для прогнозного значения
- •Пример 3.1.Исследовать зависимость объема прибыли от количества торговых точек. Сделать прогноз в предположении, что количество торговых точек будет увеличено до 25.
- •Вспомогательная расчетная таблица
- •Пример 3.2.Исследовать зависимость показателяуи факторахс помощью логарифмической, степенной и полиномиальной регрессий.
- •3.1.3. Модели рядов динамики
- •3.2. Автокорреляция данных и остатков
- •3.2.1. Автокорреляция данных
- •Пример 3.4. Исследовать на автокорреляцию динамический ряд:
- •Вспомогательная таблица для расчета коэффициента автокорреляции
- •3.2.2. Автокорреляция остатков
- •Причины возникновения автокорреляции
- •Вспомогательная таблица для расчета d-статистики
- •С помощью формулы (3.2.2) найдем d -статистику:
- •3.3. Мультиколлинеарность
- •Причины возникновения мультиколлинеарности:
- •Методы исследования мультиколлинеарности
- •Меры по устранению мультиколлинеарности:
- •3.4. Множественная линейная регрессия
- •3.4.1. Построение множественной линейной регрессии
- •Расчет элементов коэффициента
- •3.4.2. Матричный подход
- •Построение корреляционной матрицы
- •Построение модели множественной линейной регрессии и ее анализ
- •3.4.4. Нелинейные модели
- •3.4.5. Эластичность
- •4.Экспертные оценки и элементы теории графов
- •4.1. Ранговая корреляция
- •4.1.1. Экспертное оценивание
- •4.1.2. Этапы работ в системе экспертных оценок
- •4.1.3. Метод ранговой корреляции
- •Вспомогательные расчеты
- •Б) Случай многих экспертов
- •4.2. Элементы сетевого планирования
- •Основные элементы сетевого графика
- •Основные требования к сетевой модели
- •5. Индивидуальные задания для самостоятельной работы студентов по курсу “математическое моделирование”
- •5.1. Задания к разделу “Построение законов распределения”
- •5.2. Задания к разделу “Математическое программирование”
- •5.3. Задания к разделу “Регрессионный анализ”
- •Задание 2.
- •Задание 3.
- •5.4. Задания к разделу “Экспертные оценки и элементы теории графов” Задание 1.
- •Значение критерия Пирсона
- •Критерий Колмогорова
- •Критерий Колмогорова
- •Квантили распределения Стьюдента
- •Коефициентов автокорреляции
- •Литература
- •Пеніна Галина Геннадіївна, канд. Екон. Наук, доцент
Транспортная задача
Одной из часто встречающихся задач хозяйственного управления является задача по разработке рационального плана транспортных перевозок. Основная цель организации перевозок – минимизация затрат на их осуществление. Такая задача носит название транспортной.
Транспортная задача принадлежит к специальному классу распределительных задач линейного программирования. Пусть нужно перевезти однородный груз из m пунктов отправления А1, А2,…,Ат в n пунктов потребления B1, B2,…, Bп. Известны: количество груза ai (запасы), находящееся у i-го поставщика (постоянно), а также объемы потребностей в нем bj (заявки) j-го потребителя. Известны также затраты на перевозку единицы груза от i-го поставщика к j-му потребителю – тариф – сij. Необходимо распределить груз таким образом, чтобы затраты на его перевозку были минимальными.
Обозначим хij – количество груза, перевозимого из i-го пункта отправления в j-ый пункт назначения.
Решение (план перевозок)
определяется матрицей размерности (![]() )
)
 .
.
Общий вывозимый груз от поставщиков не должен превышать имеющихся у него запасов – это условие выражается системой:
х11
+ х12
+ … + х1п
![]() а1.
а1.
х21
+ х22
+ …+ х2п
![]() а2,
а2,
……………………….
хт1
+ хт2
+ … + хтп
![]() ат.
ат.
Заявки, поданные пунктами потребления, должны быть выполнены, что приводит к системе:
х11 + х21 + … + хm1 = b1.
х12 + х22 + … + хm2 = b2,
…………………………
х1т + х2т + … + хтп = bп.
Естественно, что все
неизвестные не могут принимать
отрицательные значения, т.е.
![]() .
.
Общая стоимость перевозок равна
z = c11х11+c12х12+…+c1пх1п+c21х21+c22х22+…+c2пх2п+…+cт1хт1+cт2хт2+…+cтпхтп.
Таким образом, задача
заключается в нахождении таких переменных
![]() ,
которые удовлетворяют системе ограничений
,
которые удовлетворяют системе ограничений
![]()
![]()
![]()
и обращают функцию транспортных
расходов
![]() в
минимум.
в
минимум.
Обобщая рассмотренные примеры, можно сделать следующие выводы:
ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.
линейная функция может стремиться как к максимуму, так и к минимуму.
переменные в задачах всегда неотрицательны.
В экономике задачи условной
оптимизации возникают при реализации
принципа оптимальности в планировании
и управлении, суть которого состоит в
стремлении выбрать такое планово-управленческое
решение
![]() ,
которое наилучшим образом учитывало
бы внутренние возможности и внешние
условия производственной деятельности
хозяйственного субъекта.
,
которое наилучшим образом учитывало
бы внутренние возможности и внешние
условия производственной деятельности
хозяйственного субъекта.
Реализовать на практике принцип оптимальности в планировании и управлении – это означает решить экстремальную задачу:
![]() ,
,![]() ,
или
,
или![]() ,
,![]() ,
,
где
![]() – целевая функция – математическая
запись критерия оптимальности.
– целевая функция – математическая
запись критерия оптимальности.
В задаче линейного программирования
(ЗЛП) нужно найти экстремум (максимум
или минимум) линейной целевой функции
![]() :
:
![]() ,
(2.1.1)
,
(2.1.1)
при ограничениях:
 (2.1.2)
(2.1.2)
В формулах (2.1.1), (2.1.2)
![]() – заданные постоянные величины, причем
– заданные постоянные величины, причем![]() ;
символ
;
символ![]() означает, что в конкретной ЗЛП возможно
ограничение типа равенства или неравенства
(в ту или другую сторону).
означает, что в конкретной ЗЛП возможно
ограничение типа равенства или неравенства
(в ту или другую сторону).
ЗЛП (2.1.1), (2.1.2) можно записать в следующих формах: канонической, векторной, матричной.
Каноническая форма ЗЛП имеет вид (2.1.3):
![]() ,
,
![]() ,
(2.1.3)
,
(2.1.3)
![]()
![]()
Векторная форма ЗЛП имеет вид (2.1.4):
![]() ,
,
![]() ,
(2.1.4)
,
(2.1.4)
![]() ,
,![]()
где ,

![]()
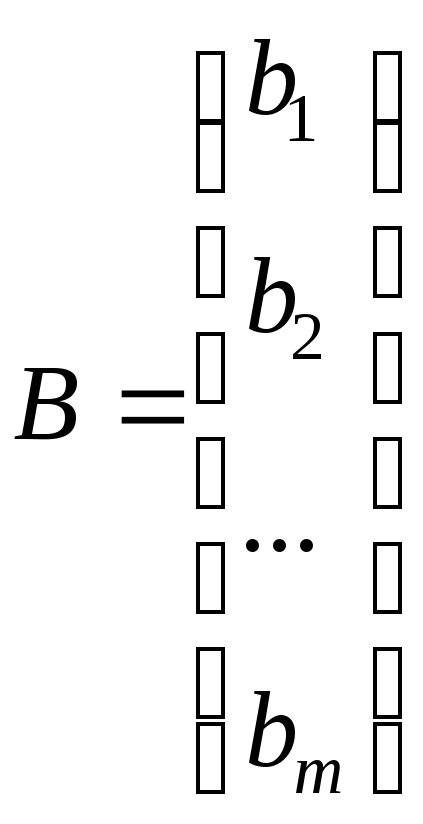 ,
,![]()
![]() .
.
Матричная форма ЗЛП имеет вид (2.1.5):
![]() ,
(2.1.5)
,
(2.1.5)
![]() ,
,![]() ,
,
где
![]()
![]() -
матрица размера
-
матрица размера![]() ,
, ,
, .
.
|
|
Планом ЗЛПилидопустимым
решением ЗЛП называется вектор |
|
|
Оптимальным планом ЗЛПилиоптимальным допустимым решением ЗЛПназываетсяплан ЗЛП, который оптимизирует целевую функцию (2.1.1). |
|
|
Областью допустимых решений ЗЛП называется совокупность точек, удовлетворяющих системе ограничений (2.1.2). |
|
|
Множество называется выпуклым, если вместе с двумя точками ему принадлежит и отрезок их соединяющий. Точка множества называется граничной, если в любой ее окрестности содержатся как точки, которые принадлежат множеству, так и точки, которые ему не принадлежат. Совокупность граничных точек множества образует его границу. Граница выпуклого многоугольника на плоскости состоит из отрезков или прямых. Точки, в которых пересекаются отрезки или прямые границы многоугольника, называются вершинами. Пересечением областейназывается множество точек, которые принадлежат каждой из этих областей. |
|
|
Выпуклой комбинациейточек многоугольника называется |
Для решения ЗЛП приведем на следующие утверждения.
|
Теорема 1. |
Область допустимых решений задачи линейного программирования является выпуклым множеством. |
|
Теорема 2. |
Оптимальное значение целевая функция задачи линейного программирования достигает в вершине многоугольника решений. |
|
Теорема 3. |
Если оптимальное значение целевая функция задачи линейного программирования достигает в нескольких точках многоугольника решений, то она принимает это же значение в любой точке, которая является их выпуклой комбинацией. |
