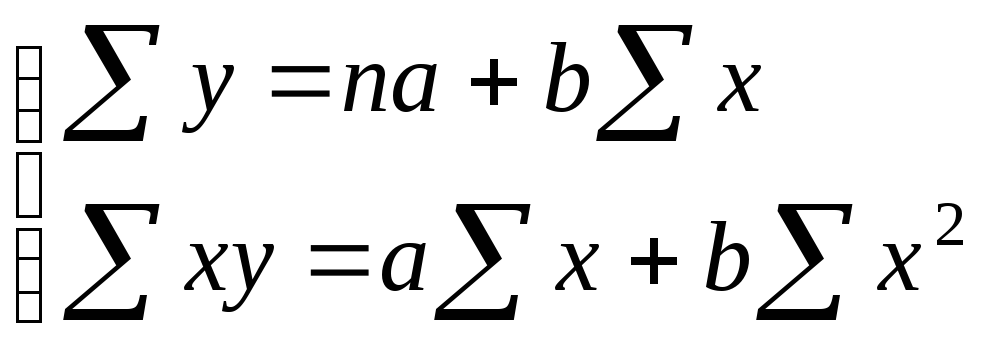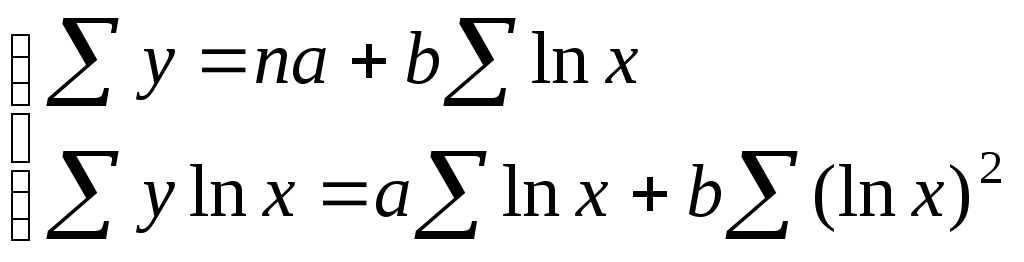3.1.3. Модели рядов динамики

Частным случаем однофакторных моделей являются модели рядов динамики, которые характеризуют развитие показателя во времени (товарооборота, объема выпуска продукции, производительности труда и т.д.).

Ряды динамики, как правило, представляют в виде таблицы. Для изображения часто ряда используют графики и диаграммы, которые позволяют заметить сложившиеся тенденции в изменении показателей. Закономерность в развитии значений ряда в одних случаях проявляется четко, в других – она может быть “размыта” за счет случайных или вполне определенных причин.

Изучая ряды динамики, стремятся выявить основную, главную тенденцию в изменении показателей. Аналитическое моделирование рядов динамики проводит с помощью тех же экономико-математических моделей, что ив случае однофакторных моделей: линейной, параболической, гиперболической, показательной, степенной, логарифмической.

Выравнивание по прямой дает эффект, как правило, в тех случаях, когда абсолютные приросты в среднем одинаковы. Параметры уравнения можно интерпретировать так: “а” – среднее значение показателя в базисном году, “b” – его средний абсолютный прирост по годам. Применение гиперболической функции целесообразно в тех случаях, когда темпы роста показателя (или его уменьшения) имеют тенденцию к снижению, а параметры выражают следующие величины: “а” – предельное значение показателя (достижимая норма), а “b” – коэффициент отклонения от нормы. Выравнивание по функции производится в основном, когда темпы роста показателя, рассчитанные по отношению к предыдущему периоду, более или менее постоянны. При этом параметр “b” характеризует средний темп роста изучаемого показателя.

Наибольшая трудность в математическом моделировании (и в выравнивании рядов динамики, в частности) заключается в выборе подходящей модели, формы аналитической зависимости. Иногда вид уравнения можно подобрать, ориентируясь на графическое изображение ряда. Иногда о типе уравнения можно судить, исходя из сути показателя. Но даже когда тенденция развития показателя известна, ее (тенденцию) можно выразить с помощью различных уравнений. Этот момент предопределяет использование нескольких моделирующих функций для выравнивания одного и того же ряда динамики с последующей их оценкой и выбором наиболее предпочтительной.

Параметры выбранных для моделирования функций можно находить различными путями. Наиболее точным приемом является метод наименьших квадратов. На его основе для каждой из функций формируют специальную систему уравнений Гаусса. Для указанных функций приведем соответствующие системы уравнений Гаусса в таблице 3.5:

Таблица 3.5

Системы уравнений Гаусса для простейших моделей

Модель	Уравнение	Система уравнений Гаусса
Линейная			(3.1.22)
Параболическая			(3.1.23)
Гиперболическая			(3.1.24)
Экспоненциальная			(3.1.25)
Степенная			(3.1.26)
Логарифмическая			(3.1.27)

В каждой из систем (3.1.26) – (3.1.31) – анализируемый показатель;– фактор времени;– количество наблюдений;– параметры моделей.

Отчет временного показателя начинают с 1. Основываясь на опытных значенияхи, определяют все суммы и подставляют их в системы, в результате чего получают системы уравнений относительно неизвестных параметров. Решая системы, находят конкретные значения параметров и подставляют их в уравнения моделирующих функций, которые должны статистически оцениваться и используются на практике.

Адекватность экономико-математической модели может быть установлена с помощью средней ошибки аппроксимации, вычисляемой по формуле (3.1.23). Выбор наиболее предпочтительной модели можно проводить на основе остаточного среднеквадратического отклонения (остаточной дисперсии), рассчитываемого по формуле (3.1.24). Оценку надежности уравнения проводят по критерию Фишера, вычисляя -статистику.

Пример 3.3. Проанализировать показатели реализации продукции на предприятии за ряд лет. Найти уравнения линейной, параболической и гиперболической, показательной, степенной и логарифмической зависимостей. Проверить адекватность полученных математических моделей, определить наилучшую модель.

Год	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Объем реализации изделий, тыс. тонн	19,1	22,9	23,7	23,9	24,5	26,6	25,7	26,1	26,2	27,6

Решение. Данные таблицы показывают, что реализация продукции неуклонно возрастала, хотя происходило это неравномерно. Очевидно, существует ряд факторов, под влиянием которых изменяется величина объема реализации. Некоторые из факторов могут действовать долгосрочно, а другие – кратковременно; некоторые могут быть важными, другие – случайными.

Составим вспомогательную расчетную таблицу 3.6 и на ее основе сформируем системы Гаусса.

Таблица 3.6

Вспомогательные расчеты для формирования систем Гаусса

х	у	x2	x3	x4	уx	yx2	1/x	1/x2	y/x
1	19,1	1	1	1	19,1	19,1	1	1	19,1
2	22,9	4	8	16	45,8	91,6	0,5	0,25	11,45
3	23,7	9	27	81	71,1	213,3	0,33333	0,11111	7,9
4	23,9	16	64	256	95,6	382,4	0,25	0,0625	5,975
5	24,5	25	125	625	122,5	612,5	0,2	0,04	4,9
6	26,6	36	216	1296	159,6	957,6	0,16666	0,02777	4,43333
7	25,7	49	343	2401	179,9	1259,3	0,14285	0,02040	3,67142
8	26,1	64	512	4096	208,8	1670,4	0,125	0,01562	3,2625
9	26,2	81	729	6561	235,8	2122,2	0,11111	0,01234	2,91111
10	27,1	100	1000	10000	271	2710	0,1	0,01	2,71
55	245,8	385	3025	25333	1409,2	10038,4	2,92896	1,54976	66,3133

Продолжение таблицы 3.6

lny	xlny	lnx	lnxlny	(lnx)2	ylnx
2,94968	2,94968	0	0	0	0
3,13113	6,26227	0,69314	2,17033	0,48045	15,8730
3,16547	9,49642	1,09861	3,47763	1,20694	26,0371
3,17387	12,6955	1,38629	4,39993	1,92181	33,1324
3,19867	15,9933	1,60943	5,14806	2,59029	39,4312
3,28091	19,6854	1,79175	5,87860	3,21040	47,6608
3,24649	22,7254	1,94591	6,31738	3,78656	50,0098
3,26193	26,0954	2,07944	6,78300	4,32407	54,2734
3,26575	29,3918	2,19722	7,17560	4,82779	57,5672
3,29953	32,9953	2,30258	7,59745	5,30189	62,4000
31,9734	178,290	15,1044	48,9480	27,6502	386,385

В последней строке таблицы 3.6 указаны суммы всех значений для каждого столбца.

Для определения параметров уравнения линейной функции запишем систему уравнений Гаусса по формуле (3.1.21):

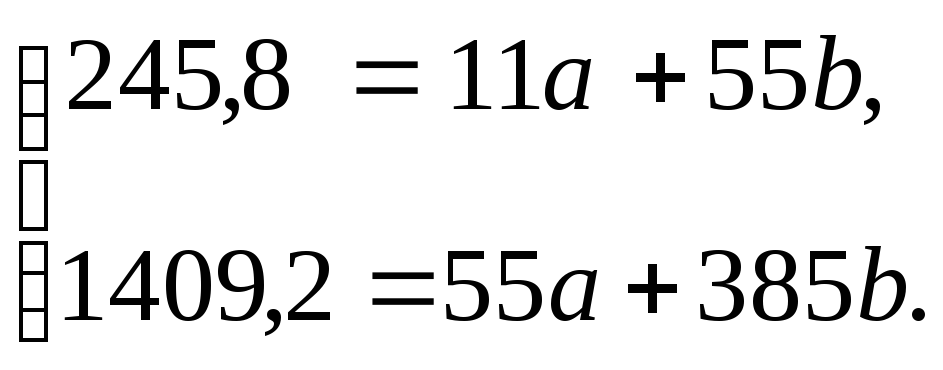
Решив эту систему, найдем = 20,76,= 0,6945. Таким образом, получим уравнение линейной модели.

Для определения параметров уравнения параболической функции запишем систему уравнений Гаусса по формуле (3.1.22):

Решив эту систему, найдем = 18,46,= 1,845,с = - 0,105. Таким образом, получим уравнение параболической модели .

Для определения параметров уравнения гиперболической функции запишем систему уравнений Гаусса по формуле (3.1.23):

Решив эту систему, найдем = 66,156,= -80,117. Таким образом, получим уравнение гиперболической модели.

Для определения параметров уравнения экспоненциальной функции запишем систему уравнений Гаусса по формуле (3.1.24):

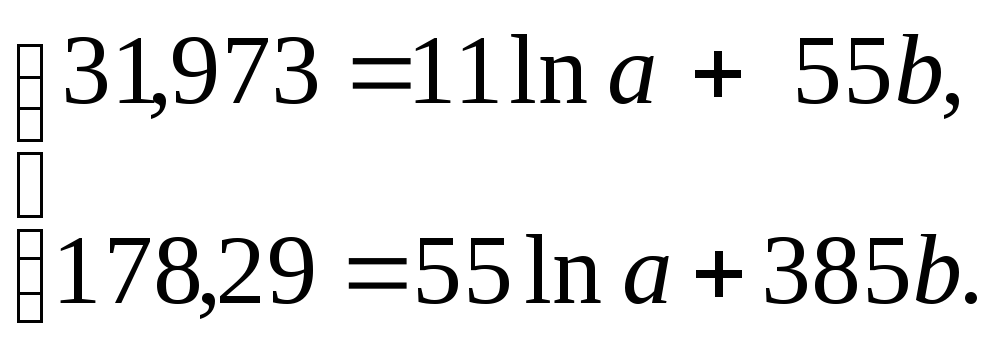
Решив эту систему, найдем = 3,034,= 0,295, тогда= 20,799. Таким образом, получим уравнение экспоненциальной модели.

Для определения параметров уравнения степенной функции запишем систему уравнений Гаусса по формуле (3.1.25):

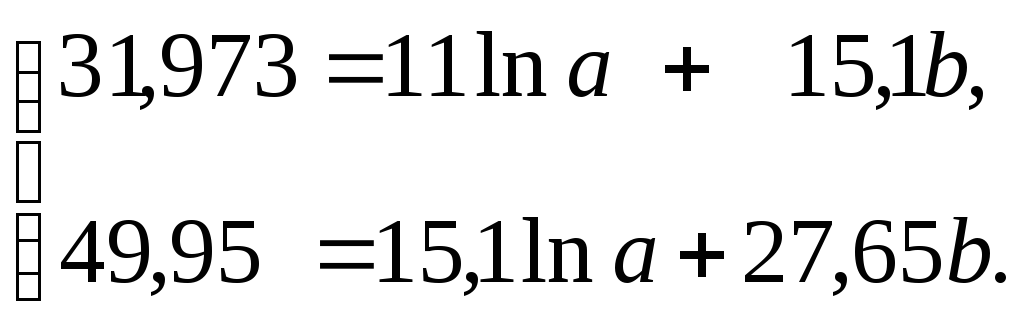
Решив эту систему, найдем = 2,993,= 0,135, тогда= 19,947. Таким образом, получим уравнение степенной модели.

Для определения параметров уравнения логарифмической функции запишем систему уравнений Гаусса по формуле (3.1.26):

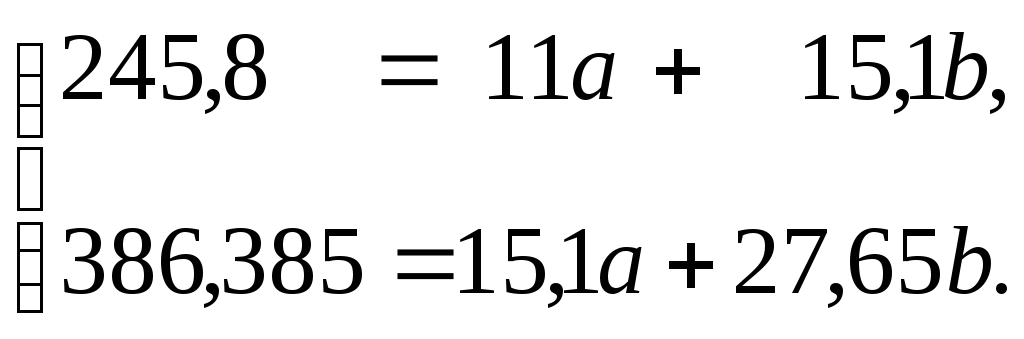
Решив эту систему, найдем = 19,858,= 3,126. Таким образом, получим уравнение логарифмической модели.

Для нахождения средней ошибки аппроксимации, остаточного среднеквадратического отклонения,- статистики для построенных моделей построим вспомогательную расчетную таблицу 3.7.

Таблица 3.7

Вспомогательная расчетная таблица

	Линейная модель				Параболическая модель				Гиперболическая модель
19,1	21,45	10,97	5,54	9,77	20,20	5,45	1,21	19,18	-13,96	236,81	1093,03	1485,41
22,9	22,15	3,39	0,56	5,91	21,73	5,38	1,37	8,12	26,10	12,25	10,22	2,30
23,7	22,84	3,75	0,73	3,02	23,05	2,81	0,42	2,33	39,45	39,92	248,07	221,13
23,9	23,54	1,54	0,13	1,09	24,17	1,10	0,07	0,17	46,13	48,19	494,03	464,26
24,5	24,23	1,10	0,07	0,12	25,07	2,27	0,32	0,24	50,13	51,13	657,03	652,94
26,6	24,93	6,71	2,80	0,12	25,77	3,24	0,70	1,40	52,80	49,62	686,61	796,55
25,7	25,62	0,31	0,01	1,08	26,25	2,10	0,30	2,79	54,71	53,03	841,62	907,86
26,1	26,32	0,82	0,05	3,01	26,53	1,61	0,18	3,79	56,14	53,51	902,48	996,12
26,2	27,01	3,00	0,66	5,91	26,60	1,49	0,16	4,06	57,25	54,24	964,36	1067,60
27,1	27,71	2,18	0,37	9,77	26,46	2,44	0,42	3,52	58,14	53,39	963,75	1126,56
24,58		33,78	10,92	39,79		27,89	5,15	45,62		652,09	6861,20	604,18

Продолжение таблицы 3.7

	Экспоненциальная модель				Степенная модель				Логарифмическая модель
19,1	21,42	10,84	5,39	9,97	19,95	4,25	0,72	21,46	19,86	3,82	0,57	22,30
22,9	22,06	3,79	0,70	6,33	21,91	4,53	0,99	7,15	22,03	3,97	0,77	6,53
23,7	22,72	4,30	0,95	3,45	23,14	2,42	0,31	2,07	23,29	1,75	0,17	1,66
23,9	23,40	2,12	0,25	1,38	24,06	0,66	0,03	0,27	24,19	1,21	0,09	0,15
24,5	24,10	1,64	0,16	0,23	24,80	1,19	0,09	0,05	24,89	1,57	0,15	0,10
26,6	24,83	7,14	3,15	0,06	25,41	4,66	1,41	0,70	25,46	4,48	1,30	0,77
25,7	25,57	0,51	0,02	0,98	25,95	0,96	0,06	1,88	25,94	0,93	0,06	1,85
26,1	26,34	0,89	0,06	3,08	26,42	1,22	0,10	3,40	26,36	0,98	0,07	3,17
26,2	27,12	3,41	0,85	6,47	26,85	2,41	0,42	5,14	26,73	1,97	0,28	4,61
27,1	27,94	2,99	0,70	11,26	27,23	0,48	0,02	7,03	27,06	0,16	0,00	6,13
24,58		37,63	12,22	43,22		22,79	4,14	49,14		20,84	3,45	47,27

В последней строке таблицы 3.7 указаны суммы всех значений соответствующих столбцов.

Для линейной модели средняя ошибка аппроксимации, найденная по формуле (3.1.23), = 33,78/10 = 3,378 меньше 5%. Значит, линейная модель адекватна фактическим данным и пригодна для дальнейшего использования. Остаточная дисперсия, рассчитанная по формуле (3.1.24) при= 2, равна 1,17. Для оценки надежности уравнения линейной модели по формуле (3.1.22), найдем-статистику:=29,16. По таблицам распределения Фишера (приложение Е) найдем= 5,32. Поскольку, то уравнение линейной модели можно считать надежным с вероятностью 0,95.

Проведя аналогичные исследования для остальных моделей, результаты представим в таблице 3.8:

Таблица 3.8

Характеристики оценки построенных моделей

Модель
Линейная	3,378	1,17	адекватна	29,16	5,32	надежна
Параболическая	2,79	0,86	адекватна	62,03	5,59	надежна
Гиперболическая	65,21	-	неадекватна	0,7	5,32	ненадежна
Экспоненциальная	3,76	1,24	адекватна	28,3	5,32	надежна
Степенная	2,28	0,72	адекватна	95,04	5,32	надежна
Логарифмическая	2,08	0,66	адекватна	109,64	5,32	надежна

Из сравнения средних ошибок аппроксимации видно, что только для гиперболической функции она выходит за 5% уровень, у остальных моделей эта характеристика не выходит за 5% уровень и приблизительно одинаковая. Если оценивать преимущество, то, очевидно, что лучшей является логарифмическая модель, поскольку у нее остаточное среднеквадратичное отклонение меньше всего.